Сколько нужно решить заданий по математике зно

Узнайте, сколько заданий по математике нужно решить для успешной сдачи ЗНО. Подробности и рекомендации для подготовки к экзамену.

Задания по математике на ЗНО — это важная часть экзамена, которая определяет уровень подготовки выпускников школы. Многие старшеклассники задаются вопросом: сколько заданий нужно решить, чтобы получить максимальный балл и успешно сдать экзамен?

Оптимальное количество заданий зависит от нескольких факторов. Во-первых, это уровень подготовки ученика. Если у вас уже хорошая математическая база и вы чувствуете уверенность в решении сложных задач, то можно смело браться за большое количество заданий.

Во-вторых, важно учитывать время, отведенное на экзамен. Задания по математике на ЗНО требуют не только математических навыков, но и умения работать быстро и точно. Поэтому, если вы замечаете, что у вас не хватает времени на решение всех заданий, лучше сконцентрироваться на наиболее сложных и важных задачах.

Оптимальное количество заданий по математике для успешной сдачи ЗНО — это индивидуальный вопрос каждого ученика. Вам следует оценить свой уровень подготовки, учесть время, отведенное на экзамен, и сделать осмысленный выбор заданий, которые вы решите. Главное — не забывайте, что подготовка к экзамену — это систематический процесс, требующий времени и усилий.

Сколько заданий по математике нужно решить на ЗНО?

Количество заданий по математике на ЗНО может варьироваться в зависимости от года и типа экзамена. Обычно на ЗНО по математике предлагается от 24 до 30 заданий. Однако, необходимо отметить, что количество заданий может меняться в разных регионах, и в некоторых случаях может быть больше или меньше.

Оптимальное количество заданий, которое нужно решить на ЗНО, зависит от уровня подготовки и времени, которое вы готовы потратить на экзамен. Если вы хорошо подготовлены и уверены в своих знаниях, то рекомендуется попытаться решить все задания, чтобы максимально показать свои способности и получить высокий балл.

Однако, если вы не уверены в своих знаниях или у вас есть ограничения по времени, то может быть разумнее сосредоточиться на решении заданий, которые вы можете выполнить быстро и верно. В таком случае, лучше отложить сложные или неясные задания на позже и сначала решить те, в которых вы уверены.

Количество заданийРекомендуемый подход

24-30	Решить все задания, если уверены в своих знаниях и есть достаточно времени
Меньше 24	Сосредоточиться на заданиях, которые вы можете выполнить быстро и верно
Больше 30	Сосредоточиться на заданиях, которые вы можете выполнить быстро и верно. Оставить сложные или неясные задания на позже, если будет время

Важно помнить, что на ЗНО по математике необходимо не только правильно решить задания, но и сделать это быстро. Поэтому, помимо количества заданий, также важно разработать стратегию решения экзамена, которая позволит вам эффективно использовать доступное время.

Определение оптимального количества заданий

Определить оптимальное количество заданий можно исходя из нескольких факторов. Во-первых, необходимо учесть время, которое отведено на экзамен. ЗНО по математике длится 180 минут, и каждое задание требует определенного времени для решения. Следовательно, количество заданий должно быть таким, чтобы оно позволяло выполнять их в установленные сроки.

Во-вторых, стоит учитывать объем материала, который нужно освоить для успешной сдачи экзамена. Чем больше заданий абитуриент решит, тем больше практики он получит и тем лучше освоит различные темы математики. Однако, не стоит забывать о качестве выполнения заданий. Скорость не всегда гарантирует правильные ответы, поэтому необходимо найти баланс между количеством и качеством.

Также стоит отметить, что каждый абитуриент имеет свои индивидуальные особенности и потребности. Некоторым может быть достаточно решить 50-60 заданий, чтобы подготовиться к экзамену, в то время как другим потребуется решить более 100 заданий. Поэтому важно учитывать свои сильные и слабые стороны, а также консультироваться с опытными преподавателями или репетиторами.

В итоге, определение оптимального количества заданий по математике на ЗНО является индивидуальным процессом. Необходимо учитывать время, объем материала, а также свои потребности и возможности. Главное – найти баланс между количеством и качеством решаемых заданий, чтобы достичь максимального результата.

Влияние количества заданий на результат

Количество заданий по математике, которые необходимо решить на ЗНО, может оказать значительное влияние на итоговый результат экзамена. Оптимальное количество заданий зависит от уровня подготовки и стратегии выполнения теста каждого конкретного участника.

С одной стороны, выполнение большего количества заданий может позволить участнику показать более широкий спектр своих знаний и навыков. Однако, слишком большая нагрузка может привести к снижению качества решения задач и усталости, что негативно отразится на результате экзамена.

С другой стороны, выполнение меньшего количества заданий может позволить участнику более тщательно рассмотреть и решить каждую задачу. Это может быть особенно полезно для тех, кто имеет проблемы с временным управлением или теми, кто хочет сосредоточиться на наиболее сложных заданиях. Однако, слишком малое количество заданий может не позволить продемонстрировать все свои знания и навыки.

Поэтому, для каждого участника ЗНО по математике важно найти оптимальное количество заданий, которое позволяет показать свои знания и навыки наилучшим образом. Это может потребовать несколько испытаний и анализа результатов предыдущих экзаменов. Однако, главное — не забывать о правильной стратегии выполнения заданий, чтобы не только решить максимальное количество задач, но и сделать это качественно.

Важно помнить:

1. Количество заданий должно быть достаточным для демонстрации своих знаний и навыков.
2. Слишком большая нагрузка может негативно сказаться на качестве решения задач.
3. Слишком малое количество заданий может не позволить продемонстрировать все свои знания.
4. Оптимальное количество заданий — это индивидуальный показатель, который нужно найти для себя.
5. Важно не только решить максимальное количество задач, но и сделать это качественно.

В конечном итоге, участнику ЗНО по математике необходимо найти баланс между количеством заданий и качеством их решения. Это поможет показать свои знания и навыки наилучшим образом и получить максимальный результат на экзамене.

Преимущества большего количества заданий

Оптимальное количество заданий на ЗНО зависит от многих факторов, таких как подготовка, уровень математических знаний, время, выделенное на экзамен. Однако, в большинстве случаев, большее количество заданий предоставляет некоторые преимущества.

Во-первых, большее количество заданий позволяет более полно оценить знания участника экзамена. Чем больше вопросов, тем более точно можно судить о его математической подготовке. Это особенно важно при сравнении результатов разных участников, когда нужно выявить самых лучших студентов.

Во-вторых, большее количество заданий дает больше возможностей для практики и применения различных математических навыков. Решение большего числа задач помогает участнику ЗНО лучше разобраться в материале, улучшить свои навыки решения задач и укрепить свои знания.

Кроме того, большее количество заданий позволяет более полно оценить уровень участника и его умение работать под давлением времени. На ЗНО участникам отводится ограниченное время на решение задач, и чем больше заданий, тем больше шансов проверить свою способность справиться с этим ограничением.

Наконец, большее количество заданий создает возможность для более глубокого погружения в математику и более широкого понимания ее применений. Чем больше задач решает участник, тем больше сможет узнать о различных областях математики и их взаимосвязях.

В целом, большее количество заданий на ЗНО имеет свои преимущества, однако необходимо учитывать индивидуальные особенности каждого участника экзамена. Важно найти баланс между количеством заданий и качеством их решения, чтобы достичь желаемого результата.

Недостатки большого количества заданий

1. Утомляемость и снижение концентрации

Большое количество заданий по математике на ЗНО может привести к утомляемости участников экзамена. Постоянное решение задач требует значительных усилий и силы воли, что может снизить концентрацию и внимание к деталям.

2. Увеличение временного давления

Чем больше заданий нужно решить, тем большее время необходимо уделить экзамену. Участники могут ощутить давление и стресс от ограниченного времени, что может негативно сказаться на их эффективности и точности решения задач.

3. Возможность ошибок и неточностей

При большом количестве заданий участники могут торопиться и допускать ошибки или неточности в решениях. Поспешность может привести к неправильным ответам и снизить общую оценку по экзамену.

4. Недостаточное понимание концепций

Большое количество заданий может ограничить возможность участников глубоко понять и освоить математические концепции. Вместо того чтобы фокусироваться на основных темах, участники могут просто стремиться решить все задачи, без полного понимания материала.

5. Уменьшение времени на самоанализ и исправление ошибок

Если участнику требуется много времени на решение задач, то останется меньше времени на самоанализ и исправление ошибок. Недостаточное время на проверку ответов может привести к упущенным ошибкам и некорректным решениям.

В целом, хотя большое количество заданий может позволить участникам показать больший объем знаний, они также имеют свои недостатки, которые должны быть учтены при разработке экзаменационных тестов.

Преимущества меньшего количества заданий

Меньшее количество заданий на ЗНО по математике может иметь некоторые преимущества для выпускников. Вот несколько из них:

• Оптимальное использование времени. Сокращение количества заданий позволяет выпускникам более эффективно распределить свое время и сконцентрироваться на каждом задании. Это помогает избежать чрезмерного напряжения и усталости, что может повысить уровень концентрации и качество работы.
• Улучшение точности ответов. Когда количество заданий сокращается, выпускникам становится доступно больше времени на каждое задание. Это позволяет им более тщательно рассмотреть условие задачи, проверить свои вычисления и ответы, что может привести к более точным результатам.
• Уменьшение стресса. Меньшее количество заданий может снизить уровень стресса, связанного с подготовкой и сдачей экзамена. Большое количество заданий может вызывать панику и затруднения в осмыслении условий задач. Сокращение количества заданий может помочь выпускникам снизить стресс и повысить уверенность в своих способностях.
• Больше времени на глубокое понимание материала. Когда выпускникам доступно больше времени на каждое задание, они могут проводить более тщательный анализ и изучение материала. Это способствует более глубокому пониманию темы и повышает уровень подготовки выпускников.
• Снижение вероятности ошибок. Сокращение количества заданий может снизить вероятность допущения ошибок и неаккуратного выполнения задач. Большое количество заданий может привести к торопливости и неосторожности, что может привести к неправильным ответам. Меньшее количество заданий позволяет выпускникам более внимательно и тщательно проводить вычисления и анализировать результаты.

Учитывая эти преимущества, меньшее количество заданий на ЗНО по математике может быть более предпочтительным для выпускников. Оно позволяет им более эффективно использовать свое время, улучшить качество своих ответов, снизить уровень стресса и повысить уровень подготовки.

Недостатки меньшего количества заданий

Участники ЗНО по математике могут столкнуться с некоторыми недостатками при решении меньшего количества заданий. Несмотря на то, что это может показаться привлекательным с точки зрения времени и усилий, есть несколько аспектов, которые следует учитывать:

1. Ограничение вариативности:

Меньшее количество заданий может ограничить возможности участников проявить свои знания и навыки в различных областях математики. Задания в ЗНО обычно охватывают широкий спектр тем, и уменьшение их числа может привести к потере возможности оценить полный спектр математических знаний участника.

2. Увеличение важности каждого задания:

При уменьшении количества заданий, каждое задание становится более важным и влияет на общую оценку участника ЗНО. Это означает, что даже небольшая ошибка может иметь существенное влияние на итоговый результат. Участники могут испытывать большее напряжение и стресс, так как ошибки могут иметь более серьезные последствия.

3. Ограничение времени и усилий:

Участники могут иметь ограниченное время на решение заданий ЗНО. Если количество заданий уменьшается, участникам может быть сложнее распределить свои усилия и время между заданиями. Они могут испытывать давление из-за необходимости сконцентрироваться на каждом задании и сделать его максимально точным и правильным.

В целом, меньшее количество заданий на ЗНО по математике имеет свои недостатки. Участники должны учитывать эти факторы при подготовке и планировании своего времени и усилий для достижения наилучших результатов.

Вопрос-ответ:

Сколько заданий по математике нужно решить на ЗНО?

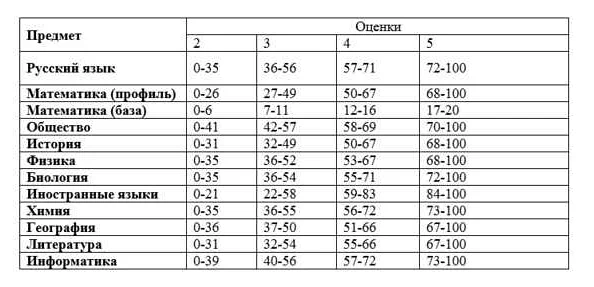
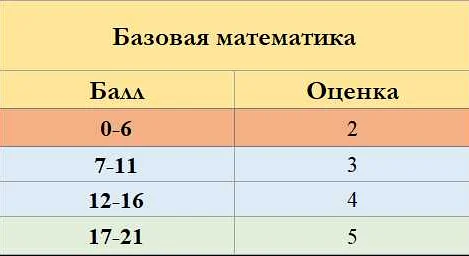
На ЗНО по математике вам предстоит решить 30 заданий.

Какое количество заданий по математике считается оптимальным для подготовки к ЗНО?

Оптимальным количеством заданий для подготовки к ЗНО по математике является решение не менее 1000 разнообразных заданий.

Сколько времени нужно на решение одного задания по математике?

Время, которое требуется на решение одного задания по математике, зависит от его сложности, но в среднем можно рассчитывать на 2-3 минуты.

Какое количество заданий по математике нужно решить для получения высокого балла на ЗНО?

Для получения высокого балла на ЗНО по математике рекомендуется решить не менее 25 заданий на 100% правильно.

Как определить оптимальное количество заданий?

Определение оптимального количества заданий по математике для подготовки к ЗНО играет важную роль в успешной сдаче экзамена. С одной стороны, количество заданий должно быть достаточным, чтобы покрыть все темы, которые могут быть представлены на экзамене. С другой стороны, избыточное количество заданий может привести к перегрузке информацией и утомлению.

Оптимальное количество заданий можно определить, учитывая следующие факторы:

• Уровень подготовки: если вы уже хорошо подготовлены и имеете хорошее понимание основных математических концепций, то вам может потребоваться меньше заданий для повторения и закрепления знаний. Если же вы начинающий ученик или испытываете трудности с определенными темами, то вам может потребоваться больше заданий для полноценной подготовки.
• Время до экзамена: если у вас есть достаточно времени до экзамена, то вы можете решать меньше заданий каждый день, но с большим вниманием и анализом решений. Если времени остается мало, то вам может потребоваться увеличить количество заданий, чтобы укрепить навыки и запомнить основные концепции.
• Уровень стресса: если вы испытываете высокий уровень стресса перед экзаменом, то может быть полезно решать больше заданий, чтобы укрепить уверенность в своих знаниях и уменьшить тревожность. Однако, не забывайте про регулярные перерывы и отдых, чтобы не перегружать себя.

Итак, оптимальное количество заданий по математике для ЗНО может варьироваться в зависимости от ваших индивидуальных потребностей и обстоятельств. Следуйте своей интуиции, регулярно оценивайте свой прогресс и планируйте свое время таким образом, чтобы достичь наилучших результатов на экзамене.

Видео по теме: