Событие математика: определение, примеры и применение

Событие математика – это событие, приуроченное к празднованию или отмечанию какого-либо события, которое связано с миром математики. Это может быть конференция, соревнование, лекция, семинар или другие мероприятия, на которых математики и любители математики могут обсуждать свои исследования, делать доклады, делиться опытом и знаниями. Узнайте больше о том, какие события математики проходят в мире и как можно принять участие в них.

Математика — это увлекательная наука, которая позволяет нам понимать и описывать мир вокруг нас. Одним из наиболее важных концептов в математике является понятие «событие». В этой статье мы рассмотрим, что такое событие, какие примеры событий можно найти в жизни, и как это понятие применяется в различных областях науки и техники.

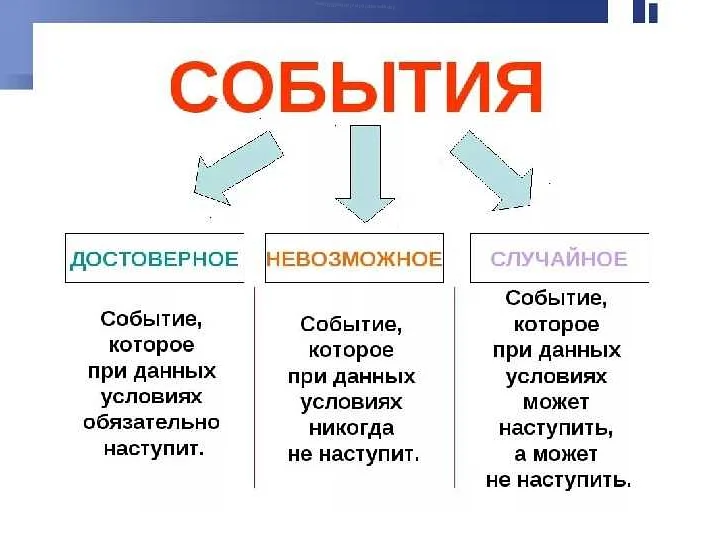
Событие — это некоторое явление, которое может произойти в определенный момент времени. Например, бросок монеты или появление пробки на дороге — это все события. В математике событие обычно описывается с помощью теории вероятностей, где мы рассматриваем вероятность того, что событие произойдет или не произойдет в определенный момент времени.

Событий много и они встречаются повсюду в нашей жизни. К примеру, события, связанные с погодой и природой (дождь, снегопад, ветер), социальными событиями (выборы, презентации), семейные события (рождение, свадьба), и множество других. Понимание событий и их вероятностей может помочь нам сделать более обоснованные выводы о будущих событиях и принимать решения на основе данных.

В науке и технике, понимание вероятностей и событий имеет огромное значение. Один из примеров — это обработка данных в компьютерах. В компьютерных системах события могут быть описаны с помощью математических моделей, которые могут помочь предсказать возможные ошибки или сбои в работе системы. Разработчики программного обеспечения используют вероятностные методы для оптимизации работы приложений и снижения риска сбоев. В медицине, вероятностные методы используются для диагностики заболеваний и проведения медицинских исследований.

Событие математика: что это?

Событие математика — это одно из ключевых понятий теории вероятностей. Оно представляет собой множество исходов, определенное на конкретном пространстве элементарных событий. Иными словами, это множество возможных результатов эксперимента, который мы рассматриваем.

Например, кинув монетку, мы получим один из двух возможных исходов: орла или решку. Событие математика в данном случае может быть определено как «выпадение орла» или «выпадение решки».

Для более сложных экспериментов, событие математика может состоять из нескольких исходов. Например, при броске двух кубиков одновременно, мы можем определить событие математика как «сумма чисел, выпавших на двух кубиках, равна 7». В данном случае, событие математика состоит из шести возможных исходов: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1).

События математика играют ключевую роль в теории вероятностей, и их понимание имеет важное значение для оценки вероятности различных событий и принятия рациональных решений в различных областях жизни, таких как финансы, бизнес и наука.

Видео по теме:

Примеры событий в математике

События в теории вероятностей

В теории вероятностей событием называется множество исходов эксперимента. Примером такого события может служить выпадение грани при бросании игральной кости. Кроме того, в теории вероятностей события могут быть условными, независимыми, дополнительными, противоположными и т.д.

События в геометрии

В геометрии событием называется некоторое логическое утверждение, которое может быть доказано или опровергнуто на основе геометрических свойств. Примерами таких событий могут служить: «Сумма углов треугольника равна 180 градусов», «Все углы прямоугольника равны между собой». Кроме того, в геометрии события могут быть связанными, разнородными, эквивалентными и т.д.

События в алгебре

В алгебре событием называется ситуация, в которой появляется некоторый элемент множества. Примерами таких событий могут являться уравнение, неравенство, система уравнений и т.д. Кроме того, в алгебре события могут быть зависимыми, независимыми, противоположными и т.д.

События в математическом анализе

В математическом анализе событием называется событие, которое характеризуется определенным поведением функции. Примерами таких событий могут служить: «точка разрыва функции», «точка минимума или максимума функции», «решение уравнения» и т.д.

Как событие математика применяется в жизни?

Математика является одним из фундаментальных наук и играет важную роль в жизни человека. Сегодня математика применяется в различных областях деятельности, таких как наука, техника, экономика, финансы, инженерия, медицина и т.д. Знания математики помогают нам понимать и решать различные задачи, а также принимать важные решения.

Одной из важнейших областей применения математики является финансовая сфера. Благодаря математическим моделям и алгоритмам мы можем прогнозировать изменения на фондовых рынках, определять риски инвестиций и разрабатывать стратегии финансового менеджмента.

Математика также широко используется в технике и инженерии. Например, при проектировании зданий и мостов, анализе и оптимизации процессов производства, разработке новых материалов и технологий. В медицине математика помогает в моделировании биологических систем, исследовании генетических свойств, анализе медицинских данных и т.д.

Еще одним примером применения математики в жизни является использование машинного обучения и искусственного интеллекта. Они позволяют автоматизировать процессы и принимать решения на основе большого объема данных.

Таким образом, математика играет важную роль в жизни современного человека и имеет широкое применение в различных областях деятельности.

Вопрос-ответ:

Что такое событие математика?

Событие в математике — это любой исход эксперимента или опыта. То есть, это возможный результат, который может произойти при проведении математического эксперимента или ситуации. Каждое событие имеет свою вероятность. Например, выпадение орла или решки при подбрасывании монеты — это два разных события.

Какие примеры можно привести в качестве событий математики?

Примеры событий в математике включают в себя: выпадение определенного числа на игральной кости, подбрасывание монеты (выпадение орла или решки), выбор карты из колоды, время ожидания в очереди, количество кликов на сайте и т.д.

Каким образом события математики применяются в жизни?

События математики применяются в различных областях жизни, например в экономике, исследовании рынка, страховании, управлении рисками, медицине и т.д. Например, оценка вероятности возникновения определенного заболевания может помочь в разработке профилактических программ. Анализ вероятности наступления определенного события может помочь в принятии важных решений и выборе наиболее эффективных стратегий в различных областях деятельности.

Каким образом можно рассчитать вероятность события?

Вероятность события можно рассчитать, поделив количество возможных благоприятных исходов на общее количество возможных исходов. Формула вероятности P(A) = n(A) / n(S), где n(A) — количество благоприятных исходов, n(S) — общее количество исходов. Например, вероятность выпадения орла при подбрасывании монеты равна 1/2 или 50%.

Каким образом можно использовать вероятность в страховой сфере?

В страховой сфере вероятность используют для расчета страховых премий. Например, страховая компания оценивает вероятность возникновения определенного риска (например, аварии на дороге) и затем рассчитывает страховую премию, которую должен платить клиент. Чем выше вероятность возникновения риска, тем выше премия.

Как можно улучшить точность оценки вероятности?

Чтобы улучшить точность оценки вероятности, можно увеличить количество исходов и провести больше экспериментов. Например, при оценке вероятности выпадения данного числа на кости можно проводить множественные броски кости и учитывать результаты. Также можно использовать статистические методы для анализа данных.

Как можно использовать теорию вероятности для принятия решений?

Теория вероятности может помочь принимать различные решения, особенно в условиях неполной информации. Например, при выборе инвестиционной стратегии можно использовать оценку вероятности различных исходов и выбрать наиболее оптимальный вариант, учитывая риски и потенциальную прибыль. Также теория вероятности может быть полезна при принятии решений в медицине, экологии и других областях.

Вероятность событий в математике

Одно из важных понятий математики, которое широко применяется в жизни — это вероятность. Она позволяет определить, насколько вероятно наступление того или иного события.

Вероятность события выражается числом от 0 до 1, где 0 означает полную невозможность события, а 1 — его полную достоверность. Также вероятность может быть выражена в процентах, где 0% — полная невозможность, а 100% — полная достоверность.

Для вычисления вероятности события используется формула:

P(A) = n(A) / n(S)

где P(A) — вероятность события A, n(A) — число исходов, благоприятствующих событию A, n(S) — общее число исходов.

Примеры применения вероятности в жизни могут быть различными: от расчета вероятности выигрыша в лотерее до прогнозирования погоды. Вероятность также активно используется в статистике для анализа данных и принятия важных решений.

Формула расчета события в математике

В математике событием называют любое возможное исходное значение. Формула расчета вероятности события состоит из двух частей: числитель (включает количество благоприятных исходов) и знаменатель (общее количество исходов).

Вероятность события = количество благоприятных исходов / общее количество исходов

Например, если бросить монетку, то общее количество исходов будет два (орел или решка), а количество благоприятных исходов — один (орел или решка). Поэтому вероятность выпадения орла или решки равна 1/2 или 50%.

Важно учитывать, что вероятность события может быть от 0 до 1. Вероятность 0 означает, что событие никогда не произойдет, а вероятность 1 — что событие обязательно произойдет.

Формула расчета события в математике используется в широком спектре профессий, таких как финансы, статистика, игры и другие области деятельности. Например, в финансовой сфере вероятность может использоваться для определения риска инвестиций или других финансовых решений.

Различия между событием и исходом в математике

Событие в математике означает возможность наступления определенного исхода в определенных условиях. Например, при броске монеты событием является выпадение орла или решки.

Исход же представляет собой реализацию события. То есть, если вы бросили монету и она выпала орлом, то это и есть исход. Искомая вероятность события определяется количеством благоприятных исходов в отношении общего числа возможных исходов.

Например, если бросить игральный кубик, общее число исходов будет равно шести. При этом событием может быть выпадение любой из шести граней, а исходами будут числа, которые выпали на кубике.

Стоит отметить, что понимание различий между событием и исходом в математике помогает в дальнейшем применении теории вероятностей в реальных ситуациях. Например, это может быть полезно при расчете вероятности выигрыша в лотерее или при принятии инвестиционных решений.

Как определить независимые и зависимые события в математике?

В математике события могут быть независимыми или зависимыми. Независимые события происходят независимо друг от друга, то есть одно событие не влияет на вероятность другого. Например, бросок монеты и бросок кубика — эти события никак не связаны друг с другом.

Зависимые события, наоборот, происходят при определенных условиях или взаимоотношениях между ними. Например, вероятность выбрать белый шар из урны будет зависеть от количества белых и черных шаров в урне, поэтому выбор первого шара может повлиять на вероятность выбора следующего.

Для того, чтобы определить, являются ли события зависимыми или независимыми, нужно использовать формулы вероятности. Если вероятность одного события не влияет на вероятность другого, то они независимы. Например, если вероятность выпадения орла на монете равна 0,5, а вероятность выпадения шестерки на кубике тоже равна 0,5, то эти события независимы, так как результат одного броска не влияет на результат другого броска.

Но если результат одного события влияет на результат другого, то они зависимы. Например, если в урне 10 белых и 5 черных шаров, то вероятность выбрать белый шар на первом броске будет 10/15 или 2/3, а на втором броске — 9/14, если первый шар не был возвращен в урну. Таким образом, вероятность выбора белого шара на втором броске зависит от результата первого.

Важно учитывать, какое событие является первым, а какое вторым в зависимых событиях. При этом можно использовать таблицы взаимосвязей вероятностей, чтобы определить, есть ли между событиями зависимость и насколько она значима.

Как определить условную вероятность в математике?

Условная вероятность в математике определяется как вероятность наступления какого-то события при условии, что другое событие уже произошло или не произошло.

Для расчета условной вероятности используется формула:

P(A|B) = P(A и B) / P(B)

где P(A|B) — условная вероятность события A при условии, что произошло событие B;

P(A и B) — вероятность наступления событий А и В;

P(B) — вероятность наступления события В.

Например, если мы бросаем кубик, то вероятность выпадения шестерки равна 1/6. Если мы знаем, что кубик уже был брошен и мы знаем, что выпало четное число, то вероятность того, что выпало 6 равна 1/3 (2 из 6 возможных результатов это четные числа, а вероятность выпадения 6 при этом равна 1/2).

Условная вероятность используется в различных областях жизни, например, в статистике, экономике, медицине и т.д. Она помогает делать более точные прогнозы и принимать более обоснованные решения.

Ошибки, связанные с событиями в математике

Математика — это точная наука, но даже в ней есть место для ошибок. Особенно часто ошибки возникают при работе со событиями. Рассмотрим наиболее распространенные ошибки:

1. Необходимость учитывать все возможные исходы. При работе со событиями необходимо учитывать все возможные исходы. Например, если бросить монетку, то есть всего два возможных исхода — выпадение «орла» или «решки». Если же есть несколько монеток, то исходы могут быть разными, например, две «орлы», две «решки» или «орел» и «решка».
2. Неправильное определение вероятности. Вероятность события — это отношение числа благоприятных исходов к общему числу исходов. Однако, вероятность может быть определена неправильно, если не учесть все возможные исходы. Например, если бросить кубик, вероятность выпадения любой из шести граней одинакова. Но если бросить два кубика, их сумма может быть разной, то есть вероятность выпадения определенной суммы будет разной.
3. Неправильное использование формулы условной вероятности. Формула условной вероятности используется для расчета вероятности возможных исходов, при условии, что произошло другое событие. Однако, формула может быть неправильно применена, если не учесть все условия. Например, при расчете вероятности того, что у двух человек будет определенное генетическое заболевание, необходимо учитывать не только их гены, но и гены их родителей и предков.
4. Математические ошибки в расчетах. Наконец, при работе со событиями необходимо быть внимательным и не допускать математические ошибки в расчетах. Одна ошибка в расчетах может привести к неверному результату.

Понятие совместных и несовместных событий в математике

В математике событие — это часть исходов некоторого случайного эксперимента. Два события называются совместными, если они могут произойти одновременно. То есть, если наступление одного события не исключает наступления другого. Например, бросок монеты может закончиться выпадением орла и выпадением решки одновременно, так что события «выпадение орла» и «выпадение решки» являются совместными.

Несовместными называются события, не могут произойти одновременно. Они исключают друг друга. Например, бросок кубика не может закончиться выпадением двух чисел одновременно, так что события «выпадение числа 3» и «выпадение числа 5» являются несовместными.

Знание того, являются ли события совместными или несовместными, важно для решения многих задач вероятности. Когда события совместны, вероятность их произведения равна произведению их вероятностей. Когда они несовместны, вероятность суммы их вероятностей равна единице, то есть 1.

Также можно рассмотреть комплементарные события, которые исключают друг друга. Комплементарное событие — это событие, которое является отрицанием другого события. Например, если событие А — выпадение орла при броске монеты, то комплементарное событие не А — выпадение решки.

Применение событий в математике в повседневной жизни

Математические события являются важным инструментом для анализа вероятности различных ситуаций. В повседневной жизни мы часто сталкиваемся с событиями, которые можно описать и анализировать с помощью математических моделей.

Например, многие финансовые решения основаны на вероятностных моделях, которые используют события для принятия решений. К примеру, если вы инвестируете в акции, то вероятность того, что цена акции возрастет или упадет можно определить с помощью математической модели.

События также играют важную роль в статистике. При проведении опросов, сборе данных и анализе результатов используются вероятностные модели, основанные на определенных событиях. Например, при определении предпочтений выборщиков перед выборами использовались события типа «выборщик проголосовал за кандидата А» или «выборщик проголосовал за кандидата В».

Кроме этого, события используются в различных областях жизни, в том числе в спорте. В футболе, например, события можно определить как «забитый гол», «красная карточка» или «удар в створ ворот». Анализ этих событий помогает тренерам и командам принимать решения, улучшать тактику и достигать лучших результатов.

В целом, события играют важную роль в математике и ее применении в повседневной жизни. Понимание и анализ вероятностных моделей, основанных на событиях, помогают принимать важные решения в различных областях деятельности и достигать лучших результатов.