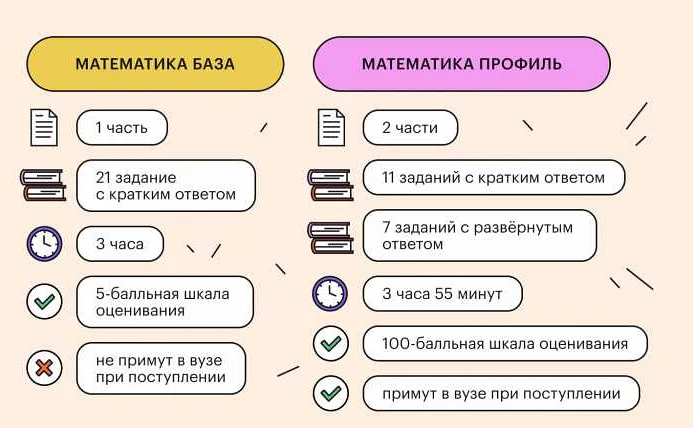
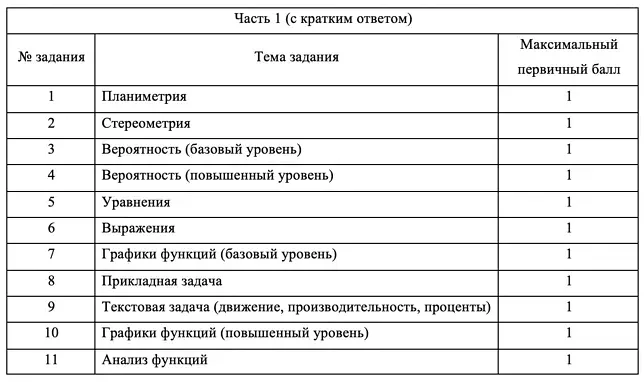
Профильная математика на ЕГЭ: полезные справочные материалы

В нашей статье вы найдете полезные материалы для подготовки к ЭГЭ по профильной математике. Решения задач, экспресс-курс, примеры решения, правила и советы учителей — все, что нужно для успешной сдачи экзамена. Рекомендации от опытных преподавателей помогут справиться со сложными темами и достичь высоких результатов!

Важным мероприятием в жизни каждого школьника является сдача ЕГЭ. Математика — один из предметов, который становится для него особенно важным, ведь именно умение решать математические задачи занимает основное место в этом экзамене. Поэтому, чтобы успешно справиться с ним, нужно не только потратить достаточно времени на подготовку, но и обладать необходимыми знаниями.

В настоящее время в сети Интернет можно найти множество ресурсов, посвященных подготовке к экзамену по математике, однако не все они являются качественными. Также многие ресурсы ориентированы на выполнение конкретных задач, но не дают полного представления о теоретической базе предмета.

В данной статье мы предлагаем ознакомиться с некоторыми справочными материалами, которые помогут преодолеть трудности при подготовке к экзамену по профильной математике. Мы собрали для вас информацию о теоретических основах, приемах решения задач и конкретных примерах, которые позволят вам укрепить свои знания и уверенно сдать экзамен.

Основы теории чисел

Теория чисел — раздел математики, изучающий свойства целых чисел. Она является одной из старейших и наиболее интересных областей математики, тесно связанной с другими ее областями, такими как алгебра и анализ.

Основополагающие понятия в теории чисел включают простые числа, наибольший общий делитель (НОД), наименьшее общее кратное (НОК), и сравнения по модулю. Эти понятия в ходе исследования образуют основу целого ряда различных теорем и закономерностей.

Простые числа — числа, которые делятся только на себя и на 1. Они играют важную роль в теории чисел, так как являются основными строительными блоками для всех целых чисел. Еще в древности было доказано, что существует бесконечное множество простых чисел.

Наибольший общий делитель (НОД) двух чисел — наибольшее целое число, которое делит оба этих числа без остатка. Для нахождения НОД используют алгоритм Евклида.

Наименьшее общее кратное (НОК) двух чисел — наименьшее положительное целое число, кратное сразу обоим этим числам.

Разбиение числа на множители и поиск простых чисел, нахождение НОД и НОК, решение сравнений и построение цепных дробей — все это и многое другое тесно связано с теорией чисел и может быть использовано в решении задач.

Видео по теме:

Алгебраические уравнения и неравенства

Алгебраические уравнения и неравенства – это базовые понятия алгебры, которые широко используются в профильной математике и ее подготовке к ЕГЭ. Уравнение – это математическое выражение, которое содержит одну или несколько переменных и знак равенства. Решением уравнения называется значение переменной или набор значений, которые при подстановке в уравнение обеспечивают истинность высказывания. Например:

x + 2 = 5

Для того, чтобы найти решение уравнения, необходимо избавиться от неизвестной переменной в правой части уравнения. Для этого необходимо вычесть из обеих частей уравнения 2:

x + 2 — 2 = 5 — 2

x = 3

Неравенство – это математическое выражение, которое содержит одну или несколько переменных и знак неравенства. Например:

x + 2 > 5

Решением неравенства называется значение переменной или набор значений, которые при подстановке в неравенство обеспечивают его истинность. Для решения неравенства, необходимо найти значение переменной, при котором левая часть неравенства будет больше правой. Например:

x + 2 — 2 > 5 — 2

x > 3

Неравенство может иметь не только знак «больше», но и «меньше», «больше или равно», «меньше или равно». Также возможны случаи, когда неравенство может быть преобразовано к эквивалентному уравнению с помощью дополнительных действий. В любом случае, знание алгебраических уравнений и неравенств является основой успеха в дальнейшем изучении математики и ее применении в повседневной жизни.

Прогрессии и последовательности

Прогрессия – последовательность чисел, в которой каждый следующий элемент получается из предыдущего прибавлением (или вычитанием) постоянной величины. Основными типами прогрессий являются арифметическая, геометрическая и гармоническая.

Арифметическая прогрессия – последовательность чисел, в которой каждый следующий элемент получается прибавлением к предыдущему числу постоянной величины d (знаменатель арифметической прогрессии).

Пример: 2, 5, 8, 11, 14, 17, … – арифметическая прогрессия с разностью d=3.

Геометрическая прогрессия – последовательность чисел, в которой каждый следующий элемент получается умножением предыдущего числа на постоянное число q (знаменатель геометрической прогрессии).

Пример: 2, 6, 18, 54, 162, 486, … – геометрическая прогрессия с знаменателем q=3.

Гармоническая прогрессия – последовательность чисел, в которой каждый следующий элемент получается прибавлением (или вычитанием) к предыдущему числу обратной величины h (знаменатель гармонической прогрессии).

Пример: 1, 1/2, 1/3, 1/4, 1/5, … – гармоническая прогрессия с знаменателем h=1.

Последовательность – набор чисел, расположенных в определенном порядке. Примером последовательности может служить ряд Фибоначчи, в котором каждый следующий элемент равен сумме двух предыдущих.

Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … – последовательность Фибоначчи.

Тригонометрия

Тригонометрия — это раздел математики, который изучает связь между углами и сторонами прямоугольного треугольника. Она имеет широкое применение в геометрии, физике, инженерии и других областях.

Основные тригонометрические функции — синус, косинус и тангенс — можно вычислить, используя соответствующие отношения между сторонами прямоугольного треугольника. По этим функциям можно построить графики, которые имеют множество приложений в научных и инженерных расчетах.

Помимо основных функций, существуют также обратные тригонометрические функции, которые позволяют находить углы по значениям тригонометрических функций. Например, арксинус — это обратная функция для синуса.

• Формула тангенса: tg α = AB/BC
• Формула косинуса: cos α = AC/BC
• Формула синуса: sin α = AB/AC

Тригонометрия является одним из основных разделов математики, и ее применение в жизни современного человека становится все более значимым. Понимание и умение применять тригонометрические функции является важным составляющим знаний в области математики и физики.

Геометрические фигуры и преобразования

Геометрические фигуры – это области плоскости или пространства, которые могут быть описаны геометрически с помощью определенных свойств и признаков. К ним относятся такие фигуры, как окружность, треугольник, квадрат, прямоугольник, круг, эллипс и многие другие.

Преобразования геометрических фигур – это изменение их положения, размера и формы с помощью определенных правил. К основным преобразованиям относятся: поворот, отражение, симметрия и сжатие-растяжение.

При повороте фигуры вокруг точки на определенный угол все ее точки смещаются по окружности, радиус которой – расстояние от точки поворота до любой точки фигуры. При отражении фигура симметрична относительно прямой, называемой осью симметрии. Также существует центральная симметрия, когда фигура симметрична относительно центра.

Сжатие-растяжение – это изменение размеров фигуры с сохранением ее формы. Все точки фигуры смещаются на одно и то же расстояние в определенном направлении.

• Окружность – геометрическая фигура, состоящая из всех точек на плоскости, расположенных на равном расстоянии от заданной точки, которая называется центром окружности.
• Треугольник – геометрическая фигура, образованная тремя отрезками, называемыми сторонами, и тремя точками их пересечения, которые называются вершинами.
• Квадрат – геометрическая фигура, у которой все стороны равны и все углы прямые.

1. Формулы для определения площади геометрических фигур:
   • Площадь круга: S = πr², где r – радиус окружности.
   • Площадь треугольника: S = ½ab·sin(α), где a и b – стороны треугольника, α – угол между ними.
   • Площадь квадрата: S = a², где a – длина стороны квадрата.
2. Формулы для нахождения периметра:
   • Периметр круга: P = 2πr, где r – радиус окружности.
   • Периметр треугольника: P = a + b + c, где a, b, c – стороны треугольника.
   • Периметр квадрата: P = 4a, где a – длина стороны квадрата.

Функции и графики

Функция — это математическое понятие, которое определяет связь между переменными. Она задаёт правило, согласно которому каждому значению одной переменной соответствует определённое значение другой переменной.

График функции — это геометрическое место точек на плоскости, координаты которых удовлетворяют заданному соотношению. Оси координат делят плоскость на четыре части, называемые квадрантами. Ось OX называется абциссой, ось OY — ординатой. На графике функции ось абсцисс представляет значения аргумента, ось ординат — соответствующие значения функции.

График функции может быть линейным, параболическим, гиперболическим и т.д. Все они имеют свои особенности. График линейной функции представляет собой прямую линию, график квадратичной функции — параболу, а график гиперболической функции — гиперболу.

• Линейная функция имеет вид y = kx + b. Здесь k — наклон прямой, а b — координата точки пересечения с осью ординат.
• Квадратичная функция имеет вид y = ax^2 + bx + c. Здесь a, b и c — коэффициенты, которые определяют форму параболы и её положение на графике.
• Гиперболическая функция имеет вид y = k/x. Здесь k — коэффициент, определяющий положение гиперболы на координатной плоскости.

Для построения графика функции необходимо найти её значения для нескольких точек и соединить их линией. Величина шага выбирается в зависимости от особенностей функции и нужна, чтобы график выглядел ровным и без «острых углов».

Точки пересечения графиков нескольких функций являются решениями уравнений, которые можно использовать в задачах. Графики функций могут быть использованы для прогнозирования изменения величин и изучения их зависимости друг от друга.

Исследование функций

Исследование функций – это процесс нахождения характеристик функции, таких как область определения, область значений, асимптоты, экстремумы, периодичность и др., с целью нахождения наиболее полной информации о ее свойствах.

Первый шаг в исследовании функций – это определение ее области определения, то есть множества значений переменной, на которых функция имеет смысл и является определенной.

Далее необходимо найти область значений функции – множество значений, которые функция может принимать. Для этого необходимо анализировать график функции или использовать методы аналитического решения.

Определение асимптот – это следующий шаг исследования функции. Асимптоты – это такие прямые, которые функция приближается все ближе и ближе по мере приближения к бесконечности или к некоторой точке. Горизонтальные асимптоты выражаются уравнением y = b, вертикальные – x = a. Обратная функция f-1(x) является асимптотой к функции f(x), если f(x) стремится к бесконечности или -бесконечности при приближении к точке f-1(x).

Определение экстремумов – это нахождение точек локального максимума или минимума функции. Эти точки могут быть найдены путем вычисления производной функции и ее обращения в нуль.

Еще одним важным параметром функции является ее периодичность. Период функции – это наименьшее положительное число T такое, что для любых значений x T+1=T, то есть, каждое T-различное значение аргумента соответствует одному и тому же значению функции.

Дифференциальное и интегральное исчисление

Дифференциальное и интегральное исчисление является базовым курсом математики для студентов экономических и технических специальностей. Этот курс изучает две важные темы: дифференцирование и интегрирование функций одной и нескольких переменных.

Дифференцирование означает нахождение производной функции, которая является ее скоростью изменения. Производная позволяет описать, как функция меняется в зависимости от изменения аргумента. Важно знать, что производные могут вычисляться для функций как аналитическим, так и графическим методами. Производные применяются в теории вероятностей, экономике, физике и других науках.

Интегрирование является обратным процессом дифференцированию. Оно позволяет найти функцию по ее производной. Интеграл функции представляет собой площадь под ее графиком. Интеграл позволяет решать задачи нахождения площадей, объемов тел, центров тяжести исследуемых объектов. Также интегралы используются в экономике, физике, биологии и других науках.

Дифференциальное и интегральное исчисление является важным инструментом математического анализа. Этот курс обеспечивает базовые знания для дальнейшего изучения более сложных математических дисциплин. Важно понимать, что математические методы находят свое применение в различных областях исследования, обеспечивая новые знания и возможности для научного и технологического прогресса.

Вероятность и статистика

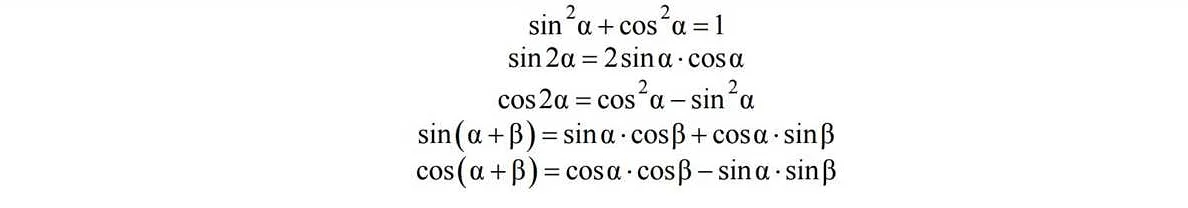
Вероятность – это наука, изучающая законы случайных явлений и процессов. Вероятность может быть выражена числами от 0 до 1: 0 означает абсолютную невозможность наступления события, 1 – абсолютную его вероятность. Все остальные значения – это вероятности, лежащие между 0 и 1.

Статистика – это наука о количественных методах сбора, обработки и анализа данных, получаемых в результате измерения различных характеристик изучаемых явлений. Статистика широко применяется в науке, экономике, бизнесе, социологии и других областях.

Вероятность и статистика тесно связаны друг с другом. Например, вероятностные методы используются для оценки различных явлений, которые имеют случайный характер. Статистические методы, в свою очередь, позволяют оценивать параметры распределения вероятностей, исследуя реальные данные о явлениях или процессах.

• Некоторые ключевые понятия, используемые в вероятности:
  • Событие. Любое возможное исходящее явление
  • Первозданные события. Неповторимые события, которые, как предполагается, имеют равную вероятность выпадения
  • Пространство элементарных событий. Множество всех элементарных событий
  • Случайная величина. Величина, которая может принимать различные значения с определенной вероятностью
• Некоторые ключевые понятия, используемые в статистике:
  • Выборка. Часть генеральной совокупности, используемая для оценки параметров
  • Математическое ожидание. Среднее значение случайной величины
  • Дисперсия. Мера разброса значений случайной величины вокруг ее математического ожидания
  • Корреляция. Степень существующей зависимости между двумя переменными

Логика и алгоритмы

Логика – это наука о законах мышления и выводов. В математике логика используется для формирования доказательств и решения задач. Она помогает устанавливать законы и правила построения алгоритмов решения задач.

Алгоритмы в математике – это последовательность строго определенных действий, которые приводят к решению задачи. Важно уметь четко формулировать условия и правила работы алгоритма, проверять его на ошибки и улучшать его эффективность.

Без логики и алгоритмов невозможен анализ и решение сложных задач, а также создание компьютерных программ и систем.

Для успешной подготовки к ЕГЭ по профильной математике необходимо усвоить базовые понятия, приемы и методы логики и алгоритмов. Нужно уметь анализировать условия задач, формулировать логические выводы, строить алгоритмы и проверять их работу на примерах.

Начиная изучение логики и алгоритмов, следует обращать внимание не только на математические аспекты, но и на их практическое применение. Решив стандартные задачи, нужно попытаться найти примеры реального применения алгоритмов в разных областях: информационных технологиях, науке, экономике, машиностроении и т.д.

Советы по подготовке к ЕГЭ по математике

1. Предварительная диагностика. Перед тем, как начинать подготовку к ЕГЭ по математике, убедитесь, что вы знаете все базовые понятия и формулы. Для этого можно пройти тест на сайте ФИПИ или воспользоваться специальными учебниками и пособиями.

2. Практика. На ЕГЭ по математике скорость выполнения заданий очень важна. Чем больше вы будете решать задач, тем лучше развиваться у вас навык расчета и практические навыки.

3. Запас времени. Важно не только знать формулы и уметь решать задачи, но и уметь делать это быстро. На экзамене вам может не хватить времени на разбор всех заданий. Поэтому рекомендуется решать задачи со временем, чтобы научиться экономить время.

• 4. Контроль времени. Для того, чтобы четко понимать, какой темп выполнения нужен, рекомендуется скачать тесты предыдущего года и прорешать их по времени. Сравните время выполнения с количеством набранных баллов и сформируйте ориентировочный распорядок экзаменационного дня.
• 5. Перерывы в процессе. На экзамене вам будет предоставлено несколько минут на перерыв. Рекомендуется использовать этот перерыв на отдых и снятие нервного напряжения. Также можно перечитать уже выполненные задания и проверить их на ошибки.

6. Самоуверенность. Важно сохранять покой и не сильно нервничать на экзамене. Уверенность в себе помогает справиться со стрессом и достичь максимального результата.

7. Обратная связь. После выполнения тестов, необходимо произвести анализ ошибок и неуверенности при решении заданий. Пересмотрите ответы и уделите особое внимание тем разделам, которые вызывают затруднения. Обязательно найдите репетитора для консультаций и проверки ошибок

Вопрос-ответ:

Какие темы математики должен знать ученик, готовящийся к ЕГЭ?

Ученик должен знать основы алгебры, геометрии, математического анализа, тригонометрии, численных методов и логики.

Где я могу найти справочные материалы по профильной математике для подготовки к ЕГЭ?

Справочные материалы можно найти в интернете на различных сайтах и форумах, в учебниках и методических пособиях, а также в специальных тестовых заданиях и банках данных.

Как эффективно использовать справочные материалы по математике для подготовки к ЕГЭ?

Для эффективного использования справочных материалов следует выделить понятные и сложные темы и посвятить им разное количество времени. Также полезно регулярно решать тестовые задания по каждому разделу математики, чтобы закрепить знания и отработать навыки решения задач.

Какие ошибки следует избегать при подготовке к ЕГЭ по математике?

Следует избегать несистематической подготовки и попыток запомнить материал без понимания. Также стоит избегать игнорирования сложных тем и недостатка практических занятий.

Какие ресурсы в интернете можно использовать для подготовки к ЕГЭ по математике?

Существует множество ресурсов, таких как онлайн-курсы, видеолекции, форумы, тестовые задания и задачники. Некоторые из них доступны бесплатно, а некоторые требуют оплаты.

Какие материалы помогут подготовиться к заданиям с использованием графиков и функций?

Помочь в подготовке к таким заданиям могут методические пособия, комплекты задач, тестовые и графические задания на различных сайтах, а также учебники, посвященные графикам и функциям.

Какие навыки необходимы для успешной подготовки к ЕГЭ по математике?

Для успешной подготовки к ЕГЭ по математике необходимо владеть навыками анализа и решения mathevznik.ru задач, уметь работать с графиками и функциями, хорошо знать основы алгебры, геометрии и математического анализа, и иметь логический склад ума.