Какой справочный материал выдается на егэ по математике базовый уровень
Содержимое
- 1 Какой справочный материал выдается на егэ по математике базовый уровень
- 1.1 Справочный материал по математике для ЕГЭ базового уровня: что использовать на экзамене
- 1.2 Формула квадратного уравнения: как применить для решения задач
- 1.3 Тригонометрические функции: основные свойства и методы применения
- 1.4 Геометрические фигуры: формулы площадей и объемов
- 1.5 Производные функций: способы нахождения и применение в задачах
- 1.6 Статистика: интерпретация данных и решение задач на выборки
- 1.7 Комбинаторика: правило умножения и сочетания в задачах
- 1.8 Векторы: основные операции и их использование в геометрии и физике
- 1.9 Вопрос-ответ:
- 1.9.0.1 Какие математические формулы я могу использовать на экзамене ЕГЭ?
- 1.9.0.2 Могу ли я использовать калькулятор на экзамене ЕГЭ по математике?
- 1.9.0.3 Какие приемы и алгоритмы решения задач мне следует знать для экзамена ЕГЭ по математике базового уровня?
- 1.9.0.4 Какие темы по математике я должен выучить для экзамена ЕГЭ базового уровня?
- 1.10 Пределы функций: способы вычисления и использование в анализе
- 1.11 Видео по теме:
Узнайте, какой справочный материал выдается на экзамене ЕГЭ по математике базового уровня. Получите информацию о доступных формулах, таблицах и примерах, которые помогут вам успешно справиться с экзаменом.
ЕГЭ по математике базового уровня – один из самых важных этапов в жизни каждого выпускника. От результата экзамена зависит поступление в вузы, выбор будущей профессии и даже возможности получить стипендию. Поэтому подготовка к этому испытанию должна быть тщательной и основательной.
На экзамене разрешается использовать справочные материалы, однако, не все учащиеся знают, что именно можно использовать. В данной статье мы расскажем о разрешенных учебных пособиях и математических таблицах, которые вы можете использовать во время экзамена.
Важно помнить, что справочный материал может быть использован только для проверки формул и определений. Решения задач и доказательства теорем в справочных материалах отсутствуют.
Среди разрешенных материалов, которые можно использовать на экзамене, следует отметить математические таблицы. В них приведены основные формулы и определения, которые могут потребоваться при решении задач. Также разрешено использование формулариев – специальных сборников формул, в которых приведены все необходимые для экзамена формулы и определения. Однако, стоит отметить, что все формулы и определения должны быть написаны собственноручно.
Также на экзамене разрешается использовать учебники с отделенными листами. Но не забывайте, что в них не должны быть записи и пометки. Важно отметить, что пользование справочными материалами не является обязательным. Чтобы успешно справиться с экзаменом, необходимо тщательно подготовиться и изучить все необходимые темы заранее.
Справочный материал по математике для ЕГЭ базового уровня: что использовать на экзамене
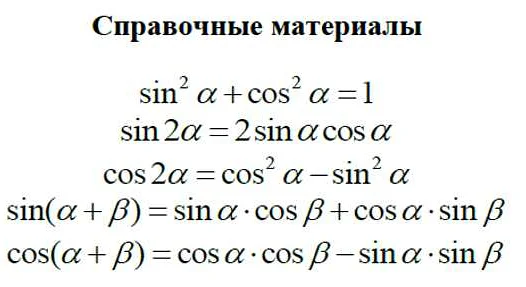
Во-первых, незаменимым инструментом на экзамене является формула квадратного уравнения. С ее помощью можно быстро и эффективно решать задачи, связанные с квадратными уравнениями. Формула квадратного уравнения имеет вид:
x = (-b ± √(b^2 — 4ac)) / 2a
где a, b и c — коэффициенты квадратного уравнения.
Во-вторых, при решении задач на нахождение площади или объема геометрических фигур полезно иметь под рукой формулы для вычисления данных величин. Например, для нахождения площади прямоугольника можно воспользоваться формулой:
S = a * b
где a и b — длины сторон прямоугольника.
В-третьих, для решения задач на проценты полезно знать формулу процентного соотношения:
P = (Часть / Целое) * 100%
где P — процент, Часть — часть от целого числа, Целое — целое число.
Кроме того, на экзамене можно использовать таблицы с основными тригонометрическими функциями, значениями стандартных углов и их синусов, косинусов и тангенсов. Такие таблицы можно найти в учебнике или распечатать заранее и взять с собой на экзамен.
Наконец, важно иметь под рукой графики функций, особенно графики элементарных функций, таких как линейная функция, квадратная функция и т.д. Графики функций могут помочь визуализировать зависимость между переменными и найти решение задачи.
В заключение, хочется отметить, что список справочных материалов, которые можно использовать на экзамене, неограничен. Главное — выбрать те материалы, которые наиболее полезны для конкретных задач и хорошо знать их, чтобы быстро и точно решать задачи.
Формула квадратного уравнения: как применить для решения задач
Формула квадратного уравнения выглядит следующим образом:
x = (-b ± √(b2 — 4ac)) / (2a)
Где x — это значение неизвестной переменной, a, b и c — коэффициенты квадратного уравнения.
Для решения задач, связанных с квадратными уравнениями, необходимо следовать нескольким шагам:
- Убедитесь, что у вас действительно квадратное уравнение. Квадратное уравнение имеет вид ax2 + bx + c = 0.
- Вычислите значения коэффициентов a, b и c из задачи.
- Используйте формулу квадратного уравнения, чтобы найти значения x.
- Убедитесь, что найденные значения x являются корнями квадратного уравнения, подставив их обратно в исходное уравнение.
Знание формулы квадратного уравнения и умение ее применять позволят вам успешно решать задачи, связанные с нахождением корней квадратного уравнения на экзамене ЕГЭ. Применяйте эту формулу в сочетании с другими математическими методами, чтобы решать сложные задачи и достигать хороших результатов.
Тригонометрические функции: основные свойства и методы применения

Основные тригонометрические функции включают синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec). Они определяются отношениями сторон прямоугольного треугольника и могут принимать значения от -1 до 1 в зависимости от угла, на который они применяются.
Основные свойства тригонометрических функций:
- Синус и косинус являются периодическими функциями с периодом 2π.
- Синус и косинус являются нечетными и четными функциями соответственно.
- Тангенс, котангенс, секанс и косеканс являются взаимнообратными функциями к синусу и косинусу.
- Тригонометрические функции можно представить через экспоненциальные функции.
Методы применения тригонометрических функций:
- Решение уравнений и систем уравнений.
- Анализ и графическое представление колебательных процессов.
- Расчеты в геометрии и физике, например, нахождение длин сторон треугольника или определение углов наклона.
- Решение задач на прямоугольник, круг и другие геометрические фигуры.
Тригонометрические функции являются важным инструментом в математике и науке. Они позволяют проводить различные расчеты и анализировать различные явления, что делает их необходимыми знаниями для успешной сдачи ЕГЭ по математике на базовом уровне.
Геометрические фигуры: формулы площадей и объемов
Во время подготовки к ЕГЭ по математике базового уровня, необходимо хорошо разбираться в геометрических фигурах и знать формулы для вычисления их площади и объема. Это позволит успешно решать задачи и получить высокий балл на экзамене.
Одна из самых простых и распространенных геометрических фигур — прямоугольник. Для него формула площади выглядит так: S = a * b, где a и b — длины сторон прямоугольника.
Треугольник имеет формулу площади: S = (a * h) / 2, где a — длина основания треугольника, а h — высота, опущенная на это основание.
Круг имеет формулу площади: S = π * r^2, где π — математическая константа, примерно равная 3,14, а r — радиус круга.
Для вычисления объема геометрических фигур также существуют соответствующие формулы.
Параллелепипед имеет формулу объема: V = a * b * h, где a, b и h — длины сторон параллелепипеда.
Цилиндр имеет формулу объема: V = π * r^2 * h, где π — математическая константа, примерно равная 3,14, r — радиус основания цилиндра, а h — высота цилиндра.
Сфера имеет формулу объема: V = (4/3) * π * r^3, где π — математическая константа, примерно равная 3,14, r — радиус сферы.
Зная эти формулы, вы сможете легко и быстро решать задачи по геометрии на ЕГЭ по математике базового уровня. Рекомендуется проводить достаточное количество практических заданий, чтобы закрепить полученные знания и уверенно сдать экзамен.
Производные функций: способы нахождения и применение в задачах
Существует несколько способов нахождения производной функции. Один из самых простых способов – использование определения производной. Для этого необходимо взять предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. Но такой способ не всегда удобен в использовании, поэтому в математике были разработаны различные правила дифференцирования, которые значительно упрощают процесс нахождения производной.
Одно из самых простых правил дифференцирования – правило константы. Согласно этому правилу, производная константы равна нулю. Также существуют правила дифференцирования для суммы, разности, произведения и частного функций. Например, производная суммы функций равна сумме их производных, производная разности функций равна разности их производных и т.д.
Производные функций находят широкое применение в решении задач. Они позволяют находить экстремумы функций, т.е. точки минимума и максимума. Например, если нужно найти наибольшую площадь прямоугольника с заданным периметром, то можно представить площадь прямоугольника как функцию его сторон и найти ее экстремум. Также производные функций используются для определения скорости изменения величин. Например, производная функции пути по времени дает скорость движения.
В заключение, производные функций являются важным инструментом в математике и находят широкое применение в различных областях. Они позволяют изучать поведение функций, находить экстремумы и определять скорость изменения величин. Знание производных функций поможет успешно справиться с задачами на ЕГЭ и в повседневной жизни.
Статистика: интерпретация данных и решение задач на выборки
Одной из основных задач статистики является работа с выборками. Выборка представляет собой подмножество данных, которые были получены при исследовании популяции. Используя выборку, можно сделать выводы о всей популяции.
Для работы с выборками используются различные статистические показатели, такие как среднее значение, медиана, мода, дисперсия и стандартное отклонение. Среднее значение — это сумма всех значений, разделенная на количество значений. Медиана — это серединное значение в упорядоченном ряду данных. Мода — это наиболее часто встречающееся значение. Дисперсия — это мера разброса данных относительно их среднего значения. Стандартное отклонение — это квадратный корень из дисперсии и показывает, насколько данные отклоняются от среднего значения.
Для решения задач на выборки можно использовать различные методы, такие как метод наименьших квадратов, критерий Стьюдента, доверительные интервалы и проверку гипотез. Метод наименьших квадратов используется для нахождения наилучшей прямой, которая аппроксимирует данные выборки. Критерий Стьюдента позволяет сравнивать средние значения двух выборок. Доверительные интервалы позволяют оценить диапазон значений, в котором с определенной вероятностью находится истинное значение параметра популяции. Проверка гипотез позволяет делать выводы о популяции на основе выборки и определенных предположений.
Использование статистических методов и показателей позволяет проводить анализ данных, делать выводы о характеристиках популяции на основе выборки и решать задачи на выборки. Хорошее знание статистики поможет успешно справиться с задачами, связанными с анализом данных, как на экзамене, так и в реальной жизни.
Комбинаторика: правило умножения и сочетания в задачах
Правило умножения позволяет определить количество возможных вариантов комбинаций, полученных путем последовательного выбора элементов из разных множеств. Если первое множество содержит m элементов, а второе множество содержит n элементов, то общее количество вариантов комбинаций будет равно m * n.
Примером задачи, решаемой с помощью правила умножения, может быть следующая ситуация: у нас есть 2 виды мороженого и 3 вида топпингов. Сколько всего разных вариантов мороженого с топпингом мы можем составить? Ответ: 2 * 3 = 6.
Сочетания представляют собой способы выбора из заданного множества определенного числа элементов без учета порядка. Формула для определения количества сочетаний из n элементов по k элементов выглядит следующим образом: Cnk = n! / (k! * (n — k)!). Здесь ! обозначает факториал числа.
Например, задача может состоять в том, чтобы определить, сколько разных команд можно сформировать из 5 человек, если в каждой команде должно быть по 3 человека. В этом случае мы используем формулу сочетаний и получаем: C53 = 5! / (3! * (5 — 3)! ) = 10.
Правило умножения и сочетания широко применяются в задачах комбинаторики на экзамене ЕГЭ базового уровня. Важно запомнить эти правила и уметь применять их для решения различных задач.
Векторы: основные операции и их использование в геометрии и физике
Основные операции над векторами включают сложение, вычитание, умножение на число и скалярное произведение.
Сложение векторов осуществляется покомпонентно: для каждой пары соответствующих компонент векторов складываются и образуют новый вектор с такими же компонентами. Например, для двух двумерных векторов AB = (a1, a2) и CD = (c1, c2), их сумма будет AB + CD = (a1 + c1, a2 + c2).
Вычитание векторов также осуществляется покомпонентно, только с вычетанием соответствующих компонент. То есть, для векторов AB и CD их разность будет AB — CD = (a1 — c1, a2 — c2).
Умножение вектора на число происходит покомпонентно: каждая компонента вектора умножается на данное число. Например, для вектора AB = (a1, a2) и числа k, умножение будет равно k * AB = (k * a1, k * a2).
Скалярное произведение двух векторов вычисляется по формуле: AB · CD = a1 * c1 + a2 * c2. Оно позволяет определить угол между векторами и вычислить проекцию одного вектора на другой.
Векторы находят широкое применение в геометрии и физике. В геометрии они используются для описания и вычисления геометрических фигур, например, для определения координат точек, задания направления движения и т.д. В физике они являются основными объектами для описания физических величин, таких как сила, сила тяжести, скорость и т.д.
ОперацияОбозначениеФормула
| Сложение векторов | AB + CD | (a1 + c1, a2 + c2) |
| Вычитание векторов | AB — CD | (a1 — c1, a2 — c2) |
| Умножение вектора на число | k * AB | (k * a1, k * a2) |
| Скалярное произведение | AB · CD | a1 * c1 + a2 * c2 |
Вопрос-ответ:
Какие математические формулы я могу использовать на экзамене ЕГЭ?
На экзамене ЕГЭ базового уровня разрешено использовать формулы для вычисления площадей и объемов геометрических фигур, формулы для вычисления процентов и среднего арифметического, формулы для решения линейных уравнений и систем линейных уравнений, формулы для вычисления площади и объема прямоугольного параллелепипеда, формулы для решения квадратных уравнений и множества других формул, указанных в учебнике.
Могу ли я использовать калькулятор на экзамене ЕГЭ по математике?
На экзамене ЕГЭ базового уровня запрещено использование калькулятора. Все вычисления необходимо производить в уме или с использованием допустимых формул и алгоритмов, указанных в учебнике.
Какие приемы и алгоритмы решения задач мне следует знать для экзамена ЕГЭ по математике базового уровня?
Для успешного выполнения задач на экзамене ЕГЭ по математике базового уровня рекомендуется знать приемы решения линейных уравнений, квадратных уравнений, неравенств, систем линейных уравнений, а также уметь вычислять проценты, строить графики функций, решать задачи на нахождение площадей и объемов геометрических фигур. Регулярное тренирование и проработка различных типов задач помогут освоить эти приемы и алгоритмы.
Какие темы по математике я должен выучить для экзамена ЕГЭ базового уровня?
Для экзамена ЕГЭ базового уровня рекомендуется изучить следующие темы: алгебраические выражения и формулы, уравнения и неравенства, системы уравнений и неравенств, функции и графики, прогрессии, математическая статистика, комбинаторика, геометрия. В каждой теме необходимо изучить основные понятия и приемы решения задач.
Пределы функций: способы вычисления и использование в анализе

Существуют различные способы вычисления пределов функций, которые позволяют найти точные значения или приближенные значения пределов. Один из самых простых способов – использование арифметических действий над пределами. Если известны пределы двух функций, то можно найти предел их суммы, разности, произведения или частного.
Еще один способ вычисления пределов – использование теоремы о сохранении знака. Если функция имеет предел и сохраняет знак при приближении аргумента к точке, то значит, предел имеет тот же знак. Этот метод особенно полезен при вычислении пределов с использованием бесконечно малых и бесконечно больших.
Пределы функций широко используются в анализе для изучения свойств функций и их поведения при стремлении аргумента к определенным значениям. Они позволяют, например, определить асимптоты функций, найти точки разрыва, исследовать поведение функций в окрестности различных точек и многое другое. Знание пределов функций позволяет более глубоко понять и анализировать математические модели и явления, что делает их незаменимыми инструментами в научной и инженерной деятельности.
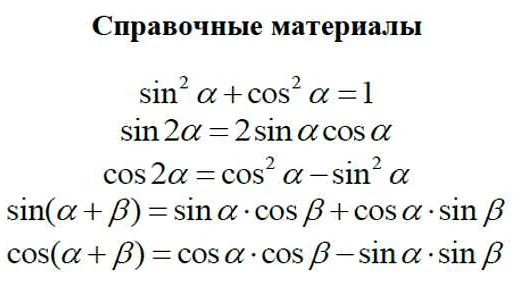

Статья очень полезна для подготовки к ЕГЭ по математике базового уровня. Она содержит исчерпывающую информацию о том, какие справочные материалы можно использовать на экзамене. Например, автор упоминает, что можно использовать формулы, таблицы и справочники по геометрии, арифметике и алгебре. Это очень важная информация, которая поможет систематизировать знания перед экзаменом. Также стоит отметить, что статья хорошо структурирована и легко читается. Заключение статьи предлагает ряд полезных советов, как использовать справочные материалы на экзамене, чтобы достичь наилучших результатов. Я уверен, что эта статья будет полезна для всех, кто готовится к ЕГЭ по математике базового уровня.
Эта статья действительно помогает мне подготовиться к ЕГЭ по математике на базовом уровне. Я нахожу здесь полезную информацию о том, какие математические инструменты разрешены на экзамене. Ведь знание этого правила может быть решающим фактором в успехе на экзамене. Я узнал, что могу использовать обычный калькулятор, но есть ограничения на функциональность, такие как наличие графического дисплея и возможности работы с символами и буквами. Кроме того, статья предоставляет справочную информацию о том, какие формулы и определения нужно запомнить и применять на экзамене. Теперь я чувствую себя более уверенно в своих знаниях и готов продолжать подготовку к ЕГЭ.