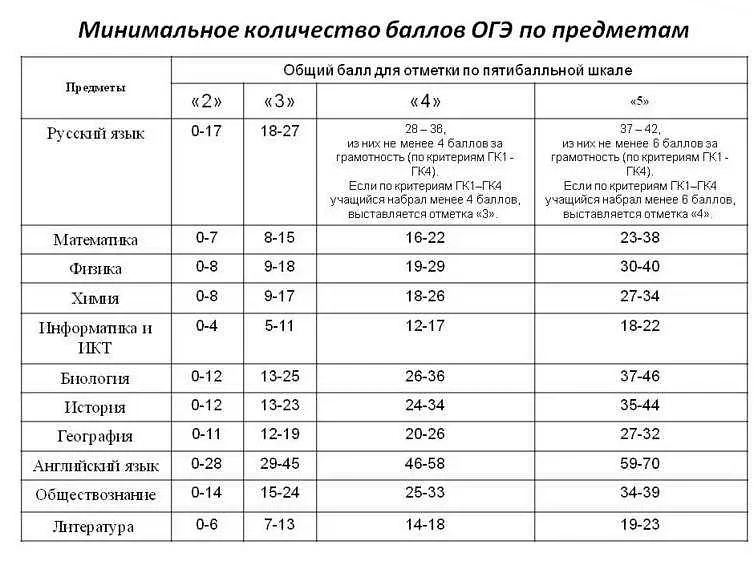
Как успешно решить задание 7 по математике на ОГЭ 2021 года?

Узнайте, как правильно решить 7 задание по математике в ОГЭ 2021 года. Мы подготовили подробную инструкцию, которая поможет вам справиться с этим заданием легко и быстро. Читайте нашу статью и получите полезные советы для подготовки к ОГЭ по математике.

ОГЭ – это экзамен, который сдают обучающиеся 9-х классов. Его цель – проверить знания учащихся по разным предметам, включая математику. В этом году в ОГЭ по математике будет 7 заданий разной сложности. Подготовка к экзамену – это ключевой момент для успеха. Как же грамотно подготовиться к ОГЭ по математике?

В этом гайде мы обсудим не только стратегии решения каждого задания, но и подскажем, как эффективно готовиться к экзамену в целом. Наш опыт показывает, что эффективность подготовки повышается, если знать программу и сдавать регулярно тесты. Также, не стоит забывать, что грамотная стратегия решения каждого задания тоже может играть ключевую роль в успехе.

Мы собрали в этом гайде лучшие стратегии решения 7 заданий по математике в ОГЭ 2021 года. Информация данная здесь проанализирована нашей командой экспертов и основана как на нашем опыте, так и на опыте успешных выпускников. Поэтому, если вы хотите сдать ОГЭ по математике на отлично – вам пригодится этот гайд.

Стратегии решения заданий ОГЭ по математике

Чтобы успешно справиться с заданиями ОГЭ по математике, необходимо использовать эффективные стратегии и подходы. Ниже представлены несколько советов по решению заданий:

• Читайте задачу внимательно и не спешите. Прежде чем приступать к решению задачи, необходимо понять, что от вас требуется. Отмечайте ключевые слова и данные, которые могут пригодиться в решении задачи.
• Рисуйте схемы и диаграммы. Использование схем и диаграмм позволит лучше представить задачу и визуализировать ее компоненты. Это поможет лучше понять ее суть и верно применить математические формулы и методы.
• Используйте логику и здравый смысл. В некоторых задачах вам могут помочь простое здравое суждение и логический подход. Если вы не можете решить задачу напрямую, подумайте, как можно переформулировать ее или рассмотреть с другой стороны.
• Работайте со всеми заданиями. Не останавливайтесь на заданиях, которые вызывают у вас трудности. Продолжайте работу и затрачивайте на каждую задачу не более 3-4 минут. Это позволит рационально распределить свое время и уложиться в отведенные рамки.
• Проверяйте свой ответ. Не забывайте проверить свои вычисления и ответы после решения каждой задачи. Это поможет избежать ошибок и допущений.

Помните, что на ОГЭ по математике важен не только правильный ответ, но и способ его получения. Поэтому обращайте внимание на решение, описывайте все этапы и используйте математические обозначения и формулы.

СоветыПримеры задач

Не паникуйте. Если вам попались задачи, которые вы не можете решить, не сдавайтесь. Прочитайте задание еще раз, попробуйте представить его визуально и использовать логический подход.	Пример: Пусть в классе 25 учеников, из которых 60% составляют девочки. Сколько девочек в классе?
Распределите свое время. Работайте со всеми заданиями, но затрачивайте на каждую не более 3-4 минут. Сконцентрируйтесь на задачах, которые вы можете решить быстро.	Пример: Два прямоугольника имеют стороны 8 см и 20 см, и 5 см и 15 см соответственно. Одинаковы ли их площади?

Основные принципы решения заданий по математике

Важно правильно понимать условие задачи. Обратите внимание на все данные и постарайтесь не пропустить важную информацию, которая может помочь в решении. Если не понятно какие-то определения или понятия, обращайтесь к формулам, примерам или теории, чтобы разобраться с сути задачи.

Далее изучите примеры и правила решения конкретного типа задач. Это позволит понять, какие методы можно использовать в решении и как найти нужные формулы. Это касается как математических, так и графических заданий.

При решении задач старайтесь работать аккуратно, тщательно проверять вычисления и не торопиться. Не бойтесь перепроверять получаемые значения и подставлять их в формулы для подтверждения корректности.

Применяйте логику и здравый смысл при решении задач. Некоторые решения могут выглядеть сложно, но решение задачи может быть проще, чем кажется на первый взгляд.

Не стесняйтесь задавать вопросы учителю, если что-то непонятно. Также не забывайте представлять ответы и решения грамотно и лаконично, с выполнением всех условий задания.

Важно не допускать ошибок при решении! Тщательная проверка всех данных и рассуждений является неотъемлемой частью верного решения задачи.

Подготовка к ОГЭ: как изучать математику

Математика требует отличный подготовки и постоянных занятий, чтобы достичь высоких результатов в ОГЭ. Основные принципы при изучении математики — это понимание и применение формул, законов и правил, а также умение решать задачи.

Важный компонент успешной подготовки к ОГЭ — это систематическое занятие математикой. Рекомендуется регулярно изучать разделы, чтобы не накапливать материал впоследствии. Можно создать расписание изучения материала и закрепления своих знаний.

Для эффективного запоминания материала рекомендуется использовать различные методы: читать теорию, решать примеры и задачи, а также повторять уже изученное материал в режиме тестирования. Это поможет запомнить основы и правила математики.

Важно знать, что упражнения, включающие решение задач, являются наиболее эффективным способом развития навыков решения задач. Нужно регулярно проверять свой уровень знаний, решая тестовые задания и упражнения.

Для подготовки к ОГЭ рекомендуется использовать различные методы обучения, такие как онлайн-курсы, учебники, видеоуроки и прочие материалы, которые помогут усвоить материал на лучшем уровне.

Важным фактором в подготовке к математическому ОГЭ является практика, которая поможет получить не только теоретические знания, но и опыт решения различных задач. Необходимо постоянно изучать разделы и решать задачи, чтобы последние дни перед ОГЭ не были для вас первыми серьезными занятиями.

Решение заданий, требующих знания формул и определений

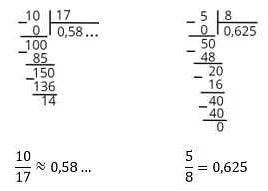
Для успешного решения заданий в ОГЭ необходимо знание формул и определений. Некоторые задания могут требовать знания определенных формул или терминов, и без их знания решить задание становится очень трудно.

Например, задание может требовать знания формулы для нахождения площади поверхности или объема тела. Для таких заданий необходимо запомнить соответствующие формулы, чтобы быстро и точно решить задание.

Также, встречаются задания, требующие знания определенных терминов, например, задание на определение вероятности события. При этом нужно знать определение вероятности, чтобы правильно решить задание.

Некоторые формулы и определения могут использоваться в нескольких заданиях, поэтому их запоминать нужно особенно внимательно. Рекомендуется выписывать формулы и определения на отдельном листе бумаги и периодически повторять их.

Иногда задания могут содержать нестандартные формулы, которые не встречались в школьной программе. В таком случае можно попросить совет у учителя или воспользоваться Интернетом для поиска объяснения.

Важно понимать, что задания, требующие знания формул и определений, могут быть разной степени сложности. Поэтому перед решением нужно внимательно прочитать условие задания и понять, какая формула или определение нужны для его решения.

Алгоритм решения заданий с графиками и таблицами

Решение заданий по математике ОГЭ с графиками и таблицами требует умения работать с этими инструментами и анализировать полученную информацию. Ниже предлагаем алгоритм, который поможет вам успешно справиться с такими заданиями.

1. Определите тип графика или таблицы. Убедитесь, что вы понимаете, что представлено на рисунке или в таблице, и какую информацию вы можете извлечь из него.
2. Анализируйте подписи и метки. Используйте подписи на графике или таблице, чтобы лучше понимать, какую информацию предоставляет каждый элемент.
3. Оцените масштаб и единицы измерения. Убедитесь, что вы понимаете масштаб и единицы измерения, используемые в графике или таблице. Выполняйте соответствующие преобразования, если необходимо.
4. Оцените тренды и паттерны. Изучите график или таблицу, чтобы найти какие-либо периодические паттерны или тренды, что может помочь в распознавании зависимостей и залежностей между переменными.
5. Составьте уравнение функции. Если график представляет собой функцию, составьте уравнение, используя информацию из графика.
6. Ответьте на вопрос или решите задачу. После анализа графика или таблицы используйте информацию, полученную в предыдущих шагах, чтобы ответить на вопрос или решить задачу.

Следуя этому алгоритму, вы можете справиться со всеми заданиями по математике ОГЭ, которые требуют работу с графиками и таблицами.

Стратегии решения задач на определение выражения функции

Для решения задач на определение выражения функции необходимо выполнить несколько шагов. Во-первых, нужно определить тип функции. Это может быть его алгебраическое выражение (например, y = 2x + 7), график (в виде точек или графического изображения) или функциональная таблица (список значений переменных x и соответствующих им значений y).

Во-вторых, следует проанализировать предоставленные данные. Для этого необходимо найти несколько точек на графике или в таблице, а также значений переменных x и y. Эти значения могут использоваться для определения коэффициентов функции и составления её алгебраического выражения.

В-третьих, стоит внимательно вычислить коэффициенты функции, которые могут быть представлены в виде чисел или переменных. Например, если функция имеет вид y = kx + b, то коэффициенты будут k и b, которые могут быть легко определены, используя найденные ранее значения x и y.

Наконец, после определения коэффициентов функции, нужно составить её алгебраическое выражение. Для этого нужно просто заменить значения коэффициентов в уравнении y = kx + b на найденные в предыдущих шагах значения.

Важно помнить, что при определении выражения функции может быть необходимо использовать дополнительные знания из математики, такие как знание алгебры, геометрии и т.д. Поэтому следует не только понимать каждый из шагов решения, но и обладать базовыми знаниями в математике в целом.

Как решать задачи на нахождение корней и дискриминанта

Задачи на нахождение корней и дискриминанта часто встречаются в заданиях по математике оценочной государственной экзамена (ОГЭ). Чтобы успешно решить такую задачу, необходимо понимать определение корня и дискриминанта.

Корень — это число, которое при подстановке в уравнение приравнивает его к нулю. К примеру, корни уравнения x^2 — 4 = 0 равны 2 и -2, так как при подстановке 2 или -2 вместо x, уравнение будет равно 0.

Дискриминант — это число, которое определяет количество корней уравнения. Если дискриминант положительный, то уравнение имеет два корня. Если дискриминант равен нулю, то уравнение имеет один корень. Если дискриминант отрицательный, то уравнение не имеет корней в области действительных чисел.

Для решения задачи на нахождение корней и дискриминанта нужно записать уравнение в стандартной форме: ax^2 + bx + c = 0. Затем нужно вычислить дискриминант по формуле D = b^2 — 4ac. Если дискриминант положительный, то корни находятся по формуле x = (-b ± √D) / 2a. Если дискриминант равен нулю, то корень находится по формуле x = (-b) / 2a. Если дискриминант отрицательный, то уравнение не имеет корней в области действительных чисел.

Важно помнить, что при решении задач на нахождение корней и дискриминанта необходимо проверять полученные ответы и избегать ошибок в расчетах. Задачи на нахождение корней и дискриминанта могут показаться сложными на первый взгляд, но с достаточной практикой и пониманием материала их можно решить успешно.

Решение задач с треугольниками и прямоугольными треугольниками

Решение задач, связанных с треугольниками и прямоугольными треугольниками, требует знания основных свойств этих фигур и умения использовать их для нахождения неизвестных величин.

Для решения задач с треугольниками необходимо помнить, что сумма углов треугольника равна 180 градусам, а сумма длин двух его сторон всегда больше, чем длина третьей стороны.

Для нахождения площади треугольника можно использовать формулу Герона: S=√p(p-a)(p-b)(p-c), где p – полупериметр треугольника, a,b,c – длины его сторон.

Для решения задач с прямоугольными треугольниками следует помнить, что катеты, примыкающие к прямому углу, обозначаются как a и b, а гипотенуза – c. Теорема Пифагора утверждает, что c^2 = a^2 + b^2. Также известно, что высота, опущенная на гипотенузу, делит ее на две части, пропорциональные катетам.

Для решения задач с прямоугольными треугольниками можно использовать также сходство треугольников, включающее отношение подобия: соответствующие стороны двух подобных треугольников имеют одинаковое отношение к соответствующим сторонам другого треугольника.

Важно уметь анализировать условие задачи, выделять существенные для решения величины и выбирать подходящие свойства треугольников и прямоугольных треугольников для решения задачи.

Секреты решения задач на вероятность и комбинаторику

Задачи на вероятность и комбинаторику являются одними из самых интересных и непредсказуемых заданий на ОГЭ по математике. Они требуют от учеников не только хорошего знания формул и правил, но и умения аккуратно и детально анализировать задачу. Ниже представлены некоторые секреты, которые помогут вам лучше понимать и решать задачи на вероятность и комбинаторику.

1) Внимательно читайте условие задачи.

Условия задач на комбинаторику могут быть довольно запутанными, поэтому важно прочитать их очень внимательно. Особое внимание следует уделить кванторам (слова «все», «некоторые», «либо»), чтобы правильно понимать, какие условия нужно учитывать в задаче.

2) Используйте таблицы, диаграммы и другие графические материалы.

Иногда условия задач на комбинаторику могут быть написаны не совсем понятно. В таком случае, полезно использовать таблицы, диаграммы и другие графические материалы для более наглядного представления условия задачи.

3) Знайте основные формулы и правила.

Для решения задач на вероятность и комбинаторику важно уметь применять основные формулы и правила. Например, формулу вероятности события, формулу количества сочетаний без повторений и т.д.

4) Работайте последовательно и с системой.

Часто бывает, что условия задач на вероятность и комбинаторику содержат многое число событий и дополнительных условий. В таком случае, лучше работать последовательно и использовать систематический подход. Например, можно начинать с вычисления количества возможных исходов и использовать эту информацию для решения задачи.

5) Смотрите ответы и проверяйте свои решения.

После решения задач на вероятность и комбинаторику, очень важно проверить ответы и убедиться, что они верны. В таком случае, можно увидеть, где была допущена ошибка, и лучше запомнить материал для будущих задач на вероятность и комбинаторику.

Решение задач на простейшие уравнения и неравенства

В ОГЭ по математике часто встречаются задачи на решение простейших уравнений и неравенств. Они просят найти значение переменной, которое удовлетворяет условию задачи. Чтобы решить такие задачи, нужно следовать определенной последовательности действий.

Первым шагом является запись условия задачи в математической форме. В задачах на уравнения нужно записать уравнение, а в задачах на неравенства — неравенство.

Далее необходимо решить уравнение или неравенство. Для этого следует использовать свойства и методы решения, которые были изучены в школе. После этого можно получить значение переменной.

Однако нужно помнить, что все решения, полученные на этом этапе, могут быть либо полными, либо частными. Чтобы проверить их правильность, нужно подставить полученное значение переменной в исходное уравнение или неравенство. Если полученное равенство или неравенство верны, то решение полное, в противном случае — частное.

Если в задаче дано несколько уравнений/неравенств, то следует выполнять вышеописанные шаги для каждого из них последовательно.

Кроме того, нужно учитывать возможное ограничение на значения переменной. Ограничение может быть дано явно или неявно, и должно быть учтено при решении задачи.

Таким образом, решение задач на простейшие уравнения и неравенства состоит из нескольких этапов: записи условия задачи, решения уравнения/неравенства, проверки полученного решения, учета ограничений и повторения этих шагов для каждого заданного уравнения/неравенства.

Решение задач на системы уравнений и неравенств

Решение задач на системы уравнений и неравенств является одним из ключевых элементов подготовки к ОГЭ по математике.

Для успешного решения задач на системы уравнений необходимо уметь:

• записывать системы уравнений в матричном виде;
• применять различные методы решения систем, такие как метод Крамера, метод Гаусса и т.д.;
• контролировать ход решения, избегая пропуска важных шагов.

При решении задач на неравенства необходимо выяснить, где находятся корни данного уравнения и провести проверку, какие значения данной переменной удовлетворяют нужным условиям. Также необходимо обращать внимание на знак неравенства, чтобы произвести корректное решение.

Важно помнить, что при решении задач на системы уравнений и неравенств необходимо быть внимательным, организованным и контролировать ход решения. Только тогда можно добиться успешного результата на ОГЭ по математике.

Вопрос-ответ:

Какие существуют основные стратегии для решения заданий по математике в ОГЭ?

Основные стратегии включают в себя освоение материала, проработка примеров, использование формул и правил раздела, выявление ключевых слов, рациональное использование времени, проверку правильности решения и выявление своих слабых мест.

Что такое ключевые слова и как их использовать для решения заданий?

Ключевые слова — это термины и понятия, которые указывают на то, каким образом необходимо решить задание. Их можно использовать для вычленения важной информации, определения неизвестных величин и применения соответствующих формул и правил. Например, если в задании есть ключевое слово «пропорциональность», то можно использовать формулу прямой пропорциональности для решения задачи.

Каким образом можно ускорить решение заданий по математике?

Для ускорения решения заданий можно использовать следующие стратегии: пропускать задания, которые требуют длительных вычислений, рационально использовать время, начиная с более простых заданий, быстро выявлять ключевые слова, не тратить время на проверку правильности каждого шага, а сначала решать задание в целом и только затем проверять его.

Что делать, если не получается решить задание?

Если не получается решить задание, не следует тратить на него слишком много времени, лучше перейти к другим заданиям и вернуться к непонятному позже. Необходимо также освоить материал, прорабатывать примеры, задавать вопросы учителю и самостоятельно анализировать собственные ошибки.

Какие ошибки чаще всего допускают при решении заданий по математике?

Чаще всего при решении заданий по математике допускают следующие ошибки: неправильный выбор формулы или правила, неверное вычисление промежуточных результатов, неправильное использование ключевых слов, неправильное чтение условия задания, ошибка в расчетах и некорректное округление чисел.

Как эффективно использовать время при решении заданий по математике?

Для эффективного использования времени необходимо рационализировать процесс решения задач: начинать со второй части, где определены более простые задания, пропускать задания, которые требуют длительных вычислений, быстро идентифицировать ключевые слова, делать заметки и краткие выкладки, быстро проверять окончательный ответ на правильность и продолжать работу до конца.

Как эффективно проверять правильность решения заданий по математике?

Для эффективной проверки правильности решения задач можно использовать следующие стратегии: использовать разные способы решения, перепроверять промежуточные вычисления, проверять правильность окончательного ответа, проверять наличие решения, проверять совпадение ответа с вариантом из ответов, проверять согласование ответа с условиями задачи.

Использование графического калькулятора при решении заданий

В процессе подготовки к ОГЭ по математике не стоит недооценивать роль графического калькулятора в решении задач.

С его помощью можно быстро и точно рассчитать значения выражений, производить операции с дробями, находить корни уравнений и многое другое. Это особенно полезно при выполнении заданий, требующих большого объёма вычислений.

Кроме того, графический калькулятор помогает в поиске графических решений задач, а это немаловажно в ситуациях, когда нужно находить графики функций или строить геометрические фигуры. С помощью калькулятора можно строить графики функций и быстро рассчитывать координаты точек при выполнении геометрических задач.

Однако не стоит забывать, что графический калькулятор – это лишь инструмент, который нужно уметь использовать правильно. Слишком усердное обращение к калькулятору может привести к тому, что ученик потеряет навыки решения задач вручную. Поэтому важно обратить внимание на баланс между использованием калькулятора и собственных знаний и умений в математике.

Итак, графический калькулятор – это незаменимый инструмент для решения задач на ОГЭ по математике, но его использование нужно дополнять знаниями и умениями решения задач вручную.

Видео по теме: