Чем связана астрономия и математика

Астрономия и математика тесно взаимосвязаны. Математические методы позволяют астрономам анализировать и предсказывать движение небесных тел и расчеты орбит, а астрономические наблюдения предоставляют математикам данные для развития новых методов и теорий. Без математики астрономия не могла бы достичь такого высокого уровня точности и предсказуемости.

Астрономия и математика являются двумя науками, которые тесно связаны друг с другом. Их взаимодействие простирается на протяжении многих веков и является основой для понимания вселенной и ее законов. Астрономия использует математические методы для анализа и интерпретации наблюдений, а математика является основой для развития новых теорий и моделей в астрономии.

С первых шагов в истории человечества, астрономы использовали математические инструменты для измерения и предсказания движения небесных тел. Они разрабатывали астрономические таблицы и формулы, чтобы точно определить положение планет, звезд и галактик на небосклоне. Кроме того, математика позволяла астрономам проанализировать различные астрономические явления, такие как солнечные и лунные затмения, и предсказывать их даты и время.

Современная астрономия невозможна без математической поддержки. Математика позволяет астрономам моделировать движение небесных тел, предсказывать будущие события, исследовать состав и структуру космических объектов, а также анализировать данные, полученные с помощью телескопов и других астрономических приборов.

Математические модели и уравнения позволяют астрономам понять физические законы, которые управляют движением планет и звезд. Они помогают исследователям предсказывать и объяснять различные астрономические явления, такие как гравитационные взаимодействия, движение комет и астероидов, эволюция звезд и галактик. Без математики астрономия была бы ограничена в своих возможностях и не смогла бы достичь таких высот в научном исследовании.

Астрономия и математика: силы взаимодействия

Одной из основных задач астрономии является определение координат и движения небесных объектов. Для этого требуется точное измерение углов и расстояний. Именно здесь математика играет важную роль. С помощью геометрических и тригонометрических методов астрономы определяют углы, а с использованием алгебры и аналитической геометрии решают задачи, связанные с движением небесных тел.

Математические методы в астрономии:Примеры применения:

Тригонометрия	Определение углов и расстояний
Геометрия	Описывание формы и размеров небесных тел
Алгебра	Решение уравнений движения планет и комет
Аналитическая геометрия	Анализ траекторий движения небесных объектов

Одним из важнейших достижений математики в астрономии является разработка Математической астрономии – области науки, которая занимается математическим описанием и моделированием движения планет и других объектов в космосе. Используя математические модели и методы, астрономы предсказывают прохождение комет и затмений, строят карты звездного неба и определяют местоположение космических аппаратов на орбите.

Таким образом, взаимодействие астрономии и математики играет ключевую роль в развитии науки о космосе. Без математического аппарата астрономы не смогли бы проводить точные измерения и анализировать данные, а без астрономии математика была бы лишена важной области приложения и развития. Вместе они образуют мощную комбинацию, которая позволяет нам лучше понимать Вселенную и ее законы.

Видео по теме:

Созвездия и геометрия: связь в небесах

Астрономы древности заметили, что звезды в определенных районах неба образуют фигуры, напоминающие различные объекты — животных, существ и предметов. Эти формы были названы созвездиями и использовались для навигации по ночному небу.

Определение формы созвездий требует использования геометрических принципов. Астрономы используют понятия прямых линий, углов и пропорций для определения границ созвездий. Они также используют математические расчеты для определения точных координат и размеров звезд внутри созвездий.

Геометрия и математика играют важную роль в астрономии. Они позволяют ученым классифицировать и идентифицировать созвездия, а также изучать их движение и эволюцию. Благодаря математике мы можем определить точные координаты звезд и предсказывать их положение на небесной сфере в будущем.

СозвездиеФорма

Большая Медведица	Волосы Девы
Орион	Орел
Скорпион	Северная Корона

Таким образом, связь между астрономией и математикой проявляется в определении формы и координат созвездий с помощью геометрических принципов и математических расчетов. Это позволяет астрономам изучать небесные объекты и расширять наши знания о Вселенной.

Математика в астрономии: открытие планет и звезд

Астрономия и математика тесно связаны друг с другом, и без применения математических методов и формул невозможно достичь значительных результатов в наблюдении и изучении космоса. Математика позволяет астрономам предсказывать и объяснять различные астрономические явления, а также открывать новые планеты и звезды.

Одним из ярких примеров применения математики в астрономии является открытие планет. Астрономы используют математические методы и модели для определения наличия планет вокруг звезды и их характеристик. Одним из таких методов является метод радиальных скоростей, основанный на измерении изменения скорости движения звезды в направлении наблюдателя. С помощью математических вычислений астрономы могут определить, есть ли планета, вращающаяся вокруг звезды, и подсчитать ее орбиту и массу.

Кроме того, математика играет важную роль в открытии и изучении звезд. Астрономы используют математические модели для определения характеристик звезд, таких как их температура, масса и возраст. Один из методов, используемых для измерения температуры звезды, называется закон Стефана-Больцмана, который связывает температуру звезды с ее светимостью. Другой метод, известный как закон Вина, позволяет определить температуру звезды по форме ее спектра.

Таким образом, математика является неотъемлемой частью астрономии и играет ключевую роль в открытии и изучении планет и звезд. Без применения математических методов и моделей астрономы не смогли бы достичь таких значительных результатов в исследовании космоса.

Вопрос-ответ:

Как связаны астрономия и математика?

Астрономия и математика имеют очень тесную связь. Математика является основой астрономии, так как позволяет астрономам анализировать данные, делать прогнозы, строить модели и решать сложные задачи. Астрономия, в свою очередь, используется в математике как источник интересных задач и примеров, которые помогают развивать новые теории и методы.

Какие математические методы используются в астрономии?

В астрономии используются различные математические методы. Например, для анализа данных и построения моделей используются статистика, вероятность, дифференциальное и интегральное исчисление, алгебраическая геометрия и другие разделы математики. Также в астрономии активно применяются численные методы, которые позволяют решать сложные уравнения и симулировать различные астрономические процессы.

Как математика помогает астрономам делать прогнозы и предсказания?

Математика позволяет астрономам анализировать и интерпретировать данные, полученные с помощью телескопов и других инструментов. С помощью математических моделей астрономы могут предсказывать движение планет, звезд и других небесных объектов, а также строить прогнозы для различных астрономических событий. Например, математические расчеты позволяют прогнозировать солнечные затмения, появление комет и другие явления.

Почему важно изучать математику для будущих астрономов?

Изучение математики является неотъемлемой частью подготовки астрономов, так как они должны уметь анализировать и интерпретировать астрономические данные, создавать и использовать математические модели, решать сложные задачи и делать прогнозы. Без хорошего знания математики астрономы не смогут полноценно работать и достичь успеха в своей профессии.

Расчеты орбит: точность и предсказуемость

Астрономия и математика тесно связаны друг с другом, особенно в контексте расчетов орбит небесных тел. Расчеты орбит играют ключевую роль в предсказании движения небесных объектов и в определении их точных позиций в пространстве.

Для расчета орбит используются сложные математические модели, такие как кеплеровы законы, которые основаны на наблюдениях и эмпирических данных. С помощью этих моделей астрономы и математики могут предсказывать движение планет, спутников и других небесных тел на большие временные промежутки.

Однако, даже с использованием точных математических моделей, расчеты орбит не всегда являются абсолютно точными. Влияние различных факторов, таких как гравитационное взаимодействие с другими телами и неоднородности в распределении массы, может привести к некоторым отклонениям от предсказанных орбит.

Тем не менее, современные методы расчета орбит обеспечивают высокую точность и предсказуемость движения небесных тел. Это позволяет астрономам и другим исследователям использовать орбитальные данные для различных научных и практических целей, таких как изучение гравитационного взаимодействия, навигация в космосе и планирование космических миссий.

Точные расчеты орбит являются фундаментальным инструментом в астрономии и имеют важное значение для понимания и исследования нашей Вселенной. Благодаря математике, мы можем предсказывать и изучать движение небесных тел, расширяя наши знания о космосе и нашей роли в нем.

Солнечная система: гравитация и математические модели

Гравитация, сила притяжения между объектами, играет ключевую роль в установлении и поддержании структуры и движения Солнечной системы. Без нее планеты не смогли бы вращаться вокруг Солнца и сохранять свои орбиты.

Математические модели являются неотъемлемой частью изучения и понимания Солнечной системы. Они позволяют ученым анализировать и прогнозировать движение планет, предсказывать события, такие как солнечные затмения и появление комет.

Математические модели основаны на законах гравитации, разработанных Исааком Ньютоном. Они учитывают массу и расстояние между небесными объектами и позволяют предсказывать их движение в прошлом, настоящем и будущем.

Использование математических моделей помогает ученым лучше понять поведение Солнечной системы, предсказывать и объяснять наблюдаемые явления и является основой для дальнейших исследований и открытий в астрономии.

Телескопы и оптика: математическое основание наблюдений

Математика играет ключевую роль в разработке и конструировании телескопов. При проектировании оптических систем необходимо решать множество математических задач, связанных с фокусными расстояниями, углами обзора, увеличением и дифракцией света.

Одним из важных элементов в оптике телескопов является зеркало или объектив. Зеркало должно быть точно отполировано и иметь заданную кривизну, чтобы собирать и фокусировать свет. Для расчета формы и размеров зеркала применяются математические модели, такие как параболическая функция.

Другим важным аспектом является объектив, который собирает свет и создает изображение в фокальной плоскости. Для расчета оптической силы объектива используется формула тонкой линзы, основанная на математической оптике.

Кроме того, математические методы применяются для определения разрешения телескопа, которое определяет его способность различать детали в наблюдаемом объекте. Разрешение зависит от размера объектива или зеркала, а также длины волны света.

Таким образом, математическое основание играет важную роль в разработке и использовании телескопов. Оно позволяет улучшить точность и разрешение наблюдений, а также оптимизировать конструкцию оптических систем. Без применения математических методов и моделей было бы сложно достичь таких результатов в астрономических исследованиях.

Галактики и расширение Вселенной: математические концепции

Одной из ключевых математических концепций, связанных с галактиками, является гравитационное взаимодействие. Законы гравитации, сформулированные Исааком Ньютоном, позволяют ученым описывать движение галактик и предсказывать их поведение в будущем.

Другой важной математической концепцией является теория относительности Альберта Эйнштейна. Эта теория описывает пространство-время и его искривление под действием массы. Она позволяет ученым изучать гравитационные линзы – явление, при котором гравитация галактик и других массивных объектов искривляет свет, проходящий через них.

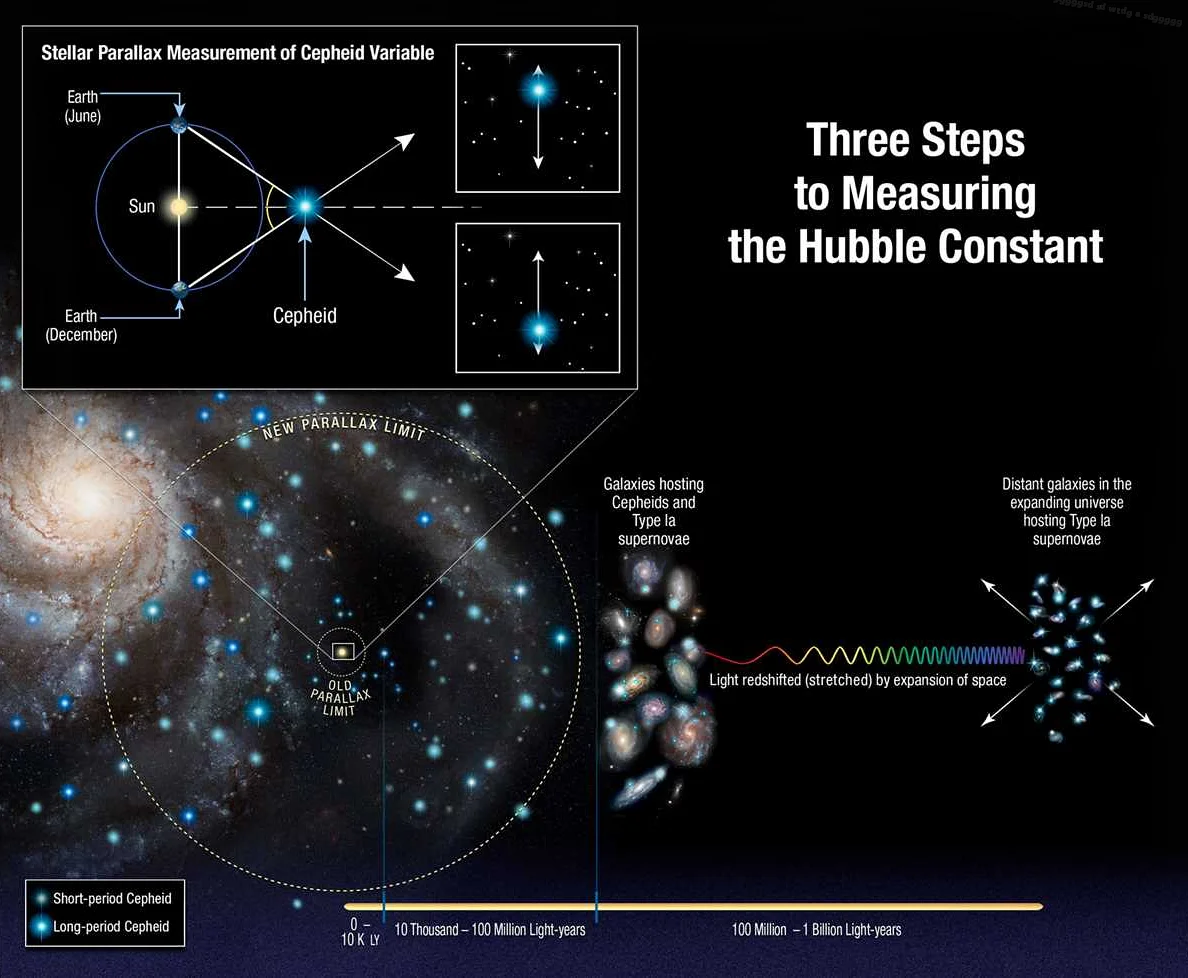
Для оценки расстояний в галактиках и измерения их скоростей используются математические модели и методы, такие как красное смещение и закон Хаббла. Красное смещение – это смещение спектральных линий в свете, испускаемом галактиками, в сторону красного конца спектра из-за расширения Вселенной. Закон Хаббла устанавливает пропорциональность между красным смещением и расстоянием между галактиками.

Прогнозирование будущего расширения Вселенной также требует математических расчетов. Для этого используются модели, такие как модель Фридмана-Леметра-Робертсона-Уокера, основанная на уравнениях Эйнштейна, и модель темной энергии, объясняющая ускорение расширения Вселенной.

Математическая концепцияЗначение

Законы гравитации	Описание движения галактик
Теория относительности	Искривление пространства-времени
Красное смещение	Измерение расстояний и скоростей галактик
Закон Хаббла	Пропорциональность расстояния и красного смещения
Модель Фридмана-Леметра-Робертсона-Уокера	Прогнозирование расширения Вселенной
Модель темной энергии	Объяснение ускорения расширения Вселенной

Черные дыры и релятивистская математика

Релятивистская математика — это математический фреймворк, разработанный Альбертом Эйнштейном, который позволяет описывать физические явления в условиях высоких скоростей и сильных гравитационных полей. Именно с помощью релятивистской математики ученые могут предсказывать и объяснять свойства черных дыр, такие как их масса, размеры и спин.

Одной из ключевых концепций релятивистской математики, используемой при изучении черных дыр, является геометрия пространства-времени. Эта геометрия описывает связь между гравитацией и распределением материи и энергии во Вселенной. Используя уравнения общей теории относительности, ученые могут моделировать и предсказывать поведение черных дыр.

Без математической основы релятивистской математики было бы невозможно понять и объяснить множество физических и астрономических явлений, включая черные дыры. Использование математических методов и уравнений позволяет ученым проводить сложные моделирования и предсказывать поведение черных дыр в различных условиях.

Таким образом, связь между астрономией и математикой проявляется в изучении черных дыр и применении релятивистской математики, которая является основой для понимания и объяснения этих загадочных астрономических объектов.

Современные исследования: числа и формулы в астрономии

Современные исследования в астрономии необоснованно нельзя представить без использования чисел и формул. Астрономы и математики работают вместе, чтобы разработать и применить сложные математические модели для анализа наблюдений и получения новых знаний о Вселенной.

Одной из основных задач астрономии является изучение дистанций до звезд и галактик. Для этого используется метод параллакса, который связывает угловую величину с астрономическими расстояниями. При проведении исследований необходимо проводить сложные вычисления и использовать специальные формулы, чтобы определить расстояние до объекта.

Астрономы также используют числа и формулы для изучения движения планет и других небесных тел. Например, законы Кеплера, сформулированные в 17 веке, описывают движение планет вокруг Солнца. Эти законы основаны на математических моделях и позволяют ученым предсказывать положение планеты в будущем.

Кроме того, астрономы используют числа и формулы для изучения свойств и состава звезд. Они анализируют спектры звездного света и используют математические модели, чтобы определить химический состав и температуру поверхности звезды.

Примеры чисел и формул, используемых в астрономии:

• Гравитационная константа (G) — используется для расчета силы гравитации между небесными телами.

• Законы Ньютона — используются для описания движения небесных тел и расчета их траекторий.

• Формула Хаббла — связывает скорость удаления галактик с их расстоянием.

• Закон Стефана-Больцмана — используется для определения яркости звезды на основе ее температуры.

• Уравнение Шредингера — используется для изучения квантовых свойств частиц в звездах и галактиках.

Таким образом, числа и формулы играют важную роль в современных исследованиях в астрономии. Они помогают астрономам анализировать данные, делать предсказания и расшифровывать сложные явления во Вселенной. Без математического подхода и использования чисел, наука об астрономии не смогла бы достичь таких высоких результатов.