Что значит три точки в математике

Три точки в математике обозначают многоточие или сумму бесконечного числа элементов. Узнайте, как использовать три точки для обозначения бесконечных последовательностей, рядов и других математических концепций.

Три точки — это символ, широко используемый в математике для обозначения различных концепций и операций. Он имеет несколько значений и применений в различных областях математики, от теории множеств до геометрии и анализа.

В теории множеств, три точки обозначают пропуск множества элементов. Например, если у нас есть множество {1, 2, 3, …}, мы можем обозначить его как {1, 2, 3, … , n}. Это означает, что множество продолжается бесконечно, и мы опускаем часть элементов.

В геометрии, три точки могут обозначать точки, лежащие на одной прямой. Это называется коллинеарностью. Если у нас есть три точки A, B и C, и они лежат на одной прямой, мы можем обозначить это как A → B → C.

В анализе, три точки могут использоваться для обозначения границы интервала или открытого промежутка на числовой оси. Например, если мы имеем интервал (a, b), где a и b являются конечными числами, мы можем обозначить его как (a, …, b).

Три точки имеют различные значения и применения в разных областях математики. Они помогают нам обозначать пропуск элементов в множествах, указывать на коллинеарность точек в геометрии и обозначать границы интервалов в анализе. Этот символ является важным инструментом для понимания и использования математических концепций и операций.

Определение и свойства точек

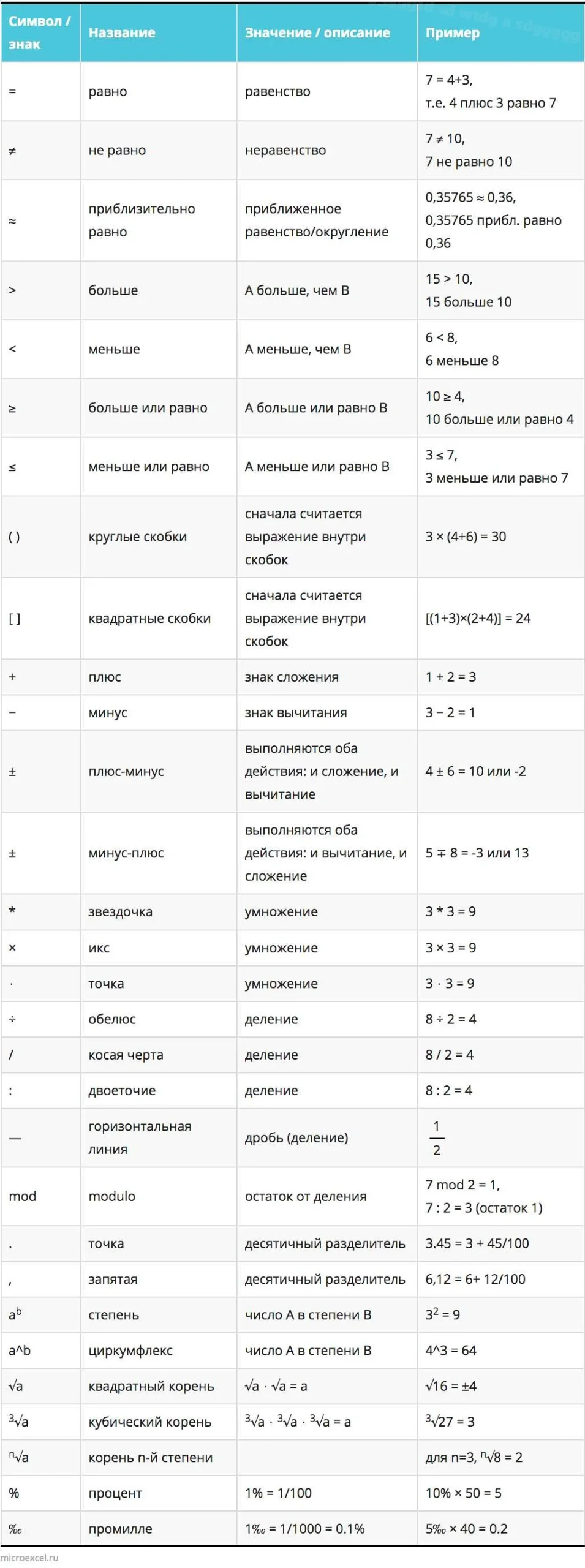
Основные свойства точек:

1. Точка не имеет размеров и не занимает места в пространстве.
2. Точка может быть определена с помощью координат на плоскости или в пространстве.
3. Любые две различные точки могут быть соединены отрезком, который является кратчайшим пути между ними.
4. Точка может быть отмечена с помощью буквы, например, точка А.
5. Точку можно перемещать без изменения ее геометрических свойств.

Точки могут быть использованы для описания геометрических фигур и объектов, таких как прямые, плоскости, окружности и тела.

Точки в геометрии

В геометрии точки используются для определения положения объектов в пространстве. Каждая точка имеет свои координаты, которые могут быть заданы на плоскости или в трехмерном пространстве.

Точки в геометрии могут быть соединены линиями, образуя отрезки, прямые и кривые. Они также могут быть использованы для определения углов, плоскостей и объемов. Множество точек, соединенных линиями, образует фигуры, такие как треугольники, квадраты, окружности и многое другое.

В геометрии точки могут быть размещены в различных положениях. Они могут быть расположены на одной прямой, составлять углы или быть внутри других фигур. Изучение точек и их положения является основой геометрии, что позволяет строить сложные геометрические модели и решать задачи по измерению и пространственному анализу.

Точки в геометрии играют важную роль в различных областях науки и техники, таких как архитектура, инженерия, компьютерная графика и другие. Они помогают определить форму и размеры объектов, создать точные модели и выполнить сложные вычисления.

В заключение, точки в геометрии являются основными строительными блоками для создания сложных геометрических фигур и моделей. Они играют важную роль в определении положения объектов в пространстве и являются важным инструментом для решения задач в различных областях человеческой деятельности.

Точки в алгебре

В алгебре точки играют важную роль в различных контекстах, таких как координатная плоскость и графики функций.

В двумерной координатной плоскости каждая точка определяется парой чисел (x, y), где x — это значение по оси абсцисс, а y — значение по оси ординат. Точки могут быть размещены в различных квадрантах плоскости в зависимости от знаков x и y.

Точки также используются для построения графиков функций. График функции представляет собой множество точек (x, f(x)), где f(x) — это значение функции при заданном x. Графики функций позволяют визуально представить свойства функций и исследовать их поведение.

Точки могут быть использованы для решения систем уравнений. Каждое уравнение системы представляет собой уравнение графика функции, и точка пересечения графиков этих функций является решением системы.

Точки также используются в векторной алгебре для задания координат векторов. Каждый вектор может быть представлен в виде направленного отрезка между двумя точками. Координаты начальной и конечной точек вектора определяют его направление и длину.

Точки в теории множеств

В теории множеств термин «точка» имеет специальное значение и используется для обозначения элементов множества. Множество может содержать различные объекты, и каждый из них называется точкой. Точки могут быть числами, буквами или другими символами, которые представляют интерес в данном контексте.

Важно отметить, что в теории множеств точки не имеют никаких внутренних свойств или структуры. Они просто являются абстрактными объектами, которые могут быть включены или исключены из множества. Использование точек в теории множеств позволяет нам формализовать и анализировать различные математические концепции и отношения.

Например, мы можем иметь множество точек {1, 2, 3}, которое содержит три целых числа. Мы можем также иметь множество точек {a, b, c}, которое содержит три буквы. В обоих случаях точки представляют отдельные элементы множества.

Точки в теории множеств также могут быть использованы для определения отношений между множествами. Например, мы можем сказать, что точка a принадлежит множеству A, обозначаемому как a ∈ A. Точка b, не принадлежащая множеству B, обозначается как b ∉ B. Такие операторы позволяют нам выражать включение и исключение элементов в контексте множества.

Точки также играют важную роль в определении операций с множествами, таких как объединение, пересечение и разность. Например, объединение двух множеств A и B, обозначается как A ∪ B, включает в себя все точки, которые принадлежат хотя бы одному из множеств. Пересечение двух множеств A и B, обозначается как A ∩ B, включает в себя только те точки, которые принадлежат обоим множествам.

Таким образом, точки в теории множеств являются основными строительными блоками для формализации и анализа различных математических концепций. Они позволяют нам оперировать с элементами множеств и определять отношения и операции между ними. Понимание роли точек в теории множеств является важным фундаментом для изучения более сложных математических концепций и их применений.

Точки в математическом анализе

В математическом анализе точки играют важную роль при определении функций, производных и интегралов. Точки могут быть использованы для обозначения значений функций на числовой оси или на графике функции.

Точка также используется для определения предела функции. Например, предел функции может быть определен как значение, к которому функция стремится, когда аргумент приближается к определенной точке на числовой оси.

В математическом анализе также существуют особые типы точек, такие как точка перегиба, точка минимума или максимума функции. Они играют важную роль в исследовании функций и определении их свойств.

Точки также могут быть использованы для обозначения вершин графиков функций. Например, вершина параболы может быть представлена в виде точки на графике.

Таким образом, точки в математическом анализе играют важную роль при определении и исследовании функций, а также при решении различных математических задач и проблем.

Точки в теории вероятности

Вероятностное пространство представляет собой тройку (Ω, F, P), где Ω — пространство элементарных исходов, F — сигма-алгебра событий, а P — вероятностная мера.

Вероятностная мера P определена на сигма-алгебре F и позволяет назначить вероятность каждому событию из F. Таким образом, точка P является мерой, которая позволяет определить вероятность наступления событий в вероятностном пространстве.

Еще одной важной точкой в теории вероятности является точка входа. Точка входа определяет начальное состояние системы и играет ключевую роль при анализе случайных процессов.

Также в теории вероятности используется понятие точки скачка. Точка скачка в случайном процессе обозначает момент времени, в котором происходит резкое изменение значения случайной величины. Точки скачка могут иметь различные интерпретации и применения в различных областях, например, в финансовой математике.

Таким образом, точки в теории вероятности играют важную роль при анализе случайных процессов и определении вероятностей событий в вероятностных пространствах.

ТочкаЗначениеПрименение

Вероятностное пространство	Определение вероятности событий	Анализ вероятностных явлений
Точка входа	Начальное состояние системы	Анализ случайных процессов
Точка скачка	Момент резкого изменения значения случайной величины	Интерпретация случайных процессов

Точки в физике

В физике точки играют важную роль и имеют различные значения и применения. Ниже приведены некоторые из них:

ТочкаЗначениеПрименение

Точка в пространстве	Абстрактное понятие без размеров, используется для описания положения объектов в пространстве	Определение координат объекта, решение задач геометрии и механики
Точка на графике	Представляет значения двух переменных, отражает связь между ними	Построение графиков функций, анализ зависимостей и трендов
Точка времени	Мгновенный момент времени, без протяженности	Описание динамики системы, измерение временных интервалов
Точка в фазовом пространстве	Представляет состояние системы в конкретный момент времени	Анализ динамического поведения систем, построение фазовых портретов

Точки имеют фундаментальное значение в физике и используются в различных областях для описания и анализа явлений и процессов.

Вопрос-ответ:

Что такое три точки в математике?

Три точки в математике обозначают эллипсис, то есть намекают на то, что после данных трех точек следует продолжение или дополнение.

Какая функция выполняют три точки в математике?

Три точки в математике выполняют функцию сокращения или сжатия информации, указывая на то, что после них есть еще данные, но их необходимо или возможно опустить для краткости.

Какие примеры применения три точки в математике?

Примеры применения три точек в математике включают использование их в математических формулах, в логических операциях, в обозначении бесконечных последовательностей и рядов, а также в сокращении и упрощении математических выражений.

Как правильно использовать три точки в математике?

Три точки следует использовать в математике тогда, когда нужно указать на продолжение или дополнение информации. Они должны быть размещены после данных, которые нужно сократить, и перед теми данными, которые хотят быть добавлены или опущены.

Видео по теме: