Что такое условный рисунок по математике
Содержимое
- 1 Что такое условный рисунок по математике
- 1.1 Рисунок в математике: основные понятия
- 1.2 Что такое условный рисунок?
- 1.3 Основные элементы условного рисунка
- 1.4 Как создать условный рисунок?
- 1.5 Примеры условных рисунков в математике
- 1.6 Применение условного рисунка в математике
- 1.7 Важность условного рисунка в обучении
- 1.8 Вопрос-ответ:
- 1.8.0.1 Что такое условный рисунок в математике?
- 1.8.0.2 Каким образом условный рисунок помогает в решении математических задач?
- 1.8.0.3 Какие примеры можно привести для условного рисунка в математике?
- 1.8.0.4 В каких областях математики применяется условный рисунок?
- 1.8.0.5 Какие преимущества имеет использование условного рисунка в математике?
- 1.9 Развитие навыков создания условных рисунков
- 1.10 Видео по теме:
Условный рисунок по математике — это способ представления графической информации на основе условных обозначений и символов. Он используется в различных областях математики, таких как геометрия, алгебра и статистика. Условный рисунок позволяет визуализировать математические концепции и отношения, делая их более понятными и доступными.
Условный рисунок — это графическое изображение, которое используется в математике для визуализации условий и задач. Он представляет собой графическое представление, которое помогает учащимся лучше понять математическую концепцию или задачу.
Условный рисунок может быть представлен в разных формах, таких как диаграммы, схемы, графики и т.д. Он может содержать различные элементы, такие как линии, фигуры, стрелки, цвета и текст. Эти элементы могут быть использованы для обозначения различных математических объектов, таких как числа, геометрические фигуры, операции и т.д.
Например, для решения задачи на нахождение площади треугольника можно использовать условный рисунок. В данном случае, можно нарисовать треугольник и указать его основание и высоту. Затем, можно использовать математические формулы и вычисления для нахождения площади треугольника.
Условный рисунок играет важную роль в обучении математике, так как он помогает учащимся визуализировать и лучше понять математические концепции. Он также помогает развивать навыки анализа, логики и критического мышления. Кроме того, условный рисунок может быть использован в решении различных математических задач и проблем, а также в реальной жизни для визуализации данных и информации.
Рисунок в математике: основные понятия
Основными понятиями, связанными с рисунками в математике, являются:
Геометрические фигуры: это замкнутые фигуры, образованные линиями и точками. Примерами геометрических фигур могут служить треугольники, квадраты, окружности и многие другие. Рисунки геометрических фигур помогают наглядно представить их форму, размеры и свойства.
Графики функций: это рисунки, которые отображают зависимость одной переменной от другой. На графике функции можно увидеть, как значение одной переменной изменяется при изменении другой переменной. Графики функций могут быть линейными, параболическими, экспоненциальными и т.д.
Координатная плоскость: это плоскость, на которой каждая точка имеет свои координаты. Координатная плоскость обычно представлена двумя ортогональными осями — горизонтальной осью (ось абсцисс) и вертикальной осью (ось ординат). Рисунки на координатной плоскости позволяют визуализировать графики функций и решать различные геометрические задачи.
Рисунки в математике играют важную роль в понимании и применении различных математических концепций. Они помогают увидеть взаимосвязи между объектами и явлениями, а также сделать абстрактные и сложные математические идеи более доступными и понятными.
Что такое условный рисунок?
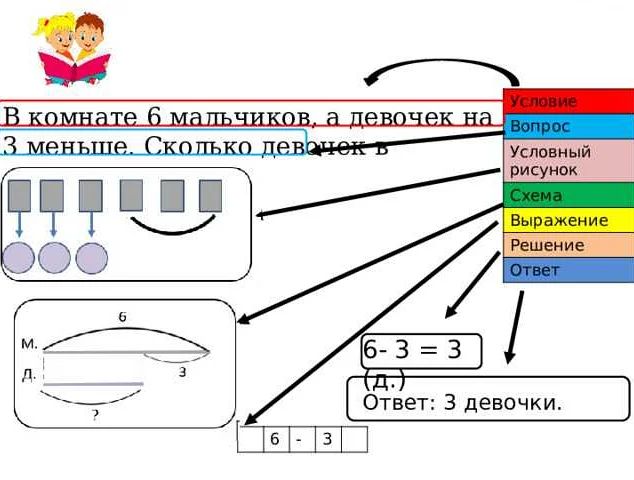
Условный рисунок состоит из графических элементов, таких как точки, линии, кривые и фигуры, которые отображают математические объекты и их взаимосвязи. Он может быть использован для изучения и применения различных математических концепций, включая функции, геометрические фигуры, преобразования и многое другое.
Условный рисунок позволяет визуально представить абстрактные математические объекты и их свойства, что упрощает их понимание и анализ. Он может быть использован для решения задач, построения графиков функций, визуализации геометрических объектов и многих других математических операций.
Применение условного рисунка в математике позволяет учащимся более глубоко понять и запомнить математические концепции и связи между ними. Он также помогает развить визуальное мышление и логическое мышление, что полезно в решении сложных задач и проблем.
Использование условного рисунка может быть полезным как для учащихся, так и для преподавателей. Учащиеся могут использовать его для самостоятельного изучения математики и решения задач, а преподаватели могут использовать его в качестве наглядного материала на уроках и в курсах по математике.
Важно отметить, что условный рисунок не заменяет математические вычисления и анализ, но служит важным инструментом для визуализации и понимания математических концепций.
Основные элементы условного рисунка
Основные элементы условного рисунка:
- Геометрические фигуры. В условном рисунке используются различные геометрические фигуры, такие как прямоугольники, круги, треугольники и т. д. Они служат для представления объектов и их свойств.
- Стрелки и линии. Стрелки и линии используются для указания направления, связи и отношений между объектами в условном рисунке. Они помогают читателю легче понять структуру и логику решения задачи.
- Надписи и текст. В условном рисунке применяются надписи и текст для обозначения объектов, свойств, формулирования условий задачи и объяснения шагов решения. Они помогают разъяснить содержание рисунка и сделать его более понятным.
- Цвета и шкалы. Цвета и шкалы используются для обозначения различных значений, уровней или категорий. Например, разные цвета могут указывать на разные типы объектов или их свойства, а шкалы могут отображать промежуточные значения или уровни.
- Символы и знаки. В условном рисунке могут использоваться различные символы и знаки для обозначения определенных значений, операций или действий. Например, знак «плюс» (+) может указывать на сложение, а символы «≥» или «≤» могут обозначать отношение «больше или равно» или «меньше или равно».
Все эти элементы условного рисунка объединяются вместе, чтобы создать наглядное представление математических концепций, задач и решений. Они помогают учащимся лучше понять и запомнить материал, а также применять его на практике.
Как создать условный рисунок?

Вот несколько шагов, которые помогут вам создать условный рисунок:
- Определите объект, который вы хотите изобразить. Это может быть, например, здание, дорога, река или электрическая цепь.
- Изучите условные обозначения, которые используются для изображения данного объекта. Каждый объект имеет свои собственные условные обозначения, которые могут варьироваться в зависимости от контекста.
- Нарисуйте основные контуры объекта. Используйте линии и геометрические фигуры, чтобы описать форму объекта.
- Добавьте условные обозначения к основным контурам. Используйте символы и знаки, чтобы показать различные характеристики объекта, такие как размер, материал, функции и т. д.
- Дополните рисунок дополнительными деталями, если это необходимо. Условный рисунок может быть достаточно простым, но иногда требуется добавление дополнительных элементов для более полного описания объекта.
- Проверьте и исправьте свою работу. Убедитесь, что условные обозначения корректно отображают объект и что рисунок понятен для других людей.
Создание условного рисунка требует практики и опыта, поэтому не бойтесь экспериментировать и улучшать свои навыки. С помощью условного рисунка вы сможете легче и наглядно представить сложные концепции и идеи.
Примеры условных рисунков в математике

Рассмотрим несколько примеров условных рисунков в математике:
1. Рисунок для иллюстрации геометрической фигуры:
Нарисуем правильный треугольник, который имеет все стороны одинаковой длины и все углы равными. Мы можем использовать условные обозначения, чтобы отметить длину сторон и углы треугольника.
2. Рисунок для иллюстрации алгебраической формулы:
Нарисуем график функции, заданной алгебраической формулой, например, квадратичной функции. Мы можем использовать условные обозначения, чтобы подписать оси координат, точки и линии на графике.
3. Рисунок для иллюстрации задачи на геометрическую вероятность:
Нарисуем диаграмму, чтобы проиллюстрировать вероятность событий в геометрической задаче. Мы можем использовать условные обозначения, чтобы показать различные области и их вероятности на диаграмме.
Примеры условных рисунков в математике помогают студентам визуализировать абстрактные понятия и лучше понять математические концепции. Они могут быть использованы в учебных материалах, заданиях и тестах, чтобы сделать математику более интересной и понятной.
Применение условного рисунка в математике

Применение условного рисунка в математике может быть разнообразным. Ниже приведены некоторые примеры использования условного рисунка в различных областях математики:
- В геометрии: условный рисунок может использоваться для иллюстрации геометрических фигур, свойств углов, теорем и доказательств геометрических утверждений.
- В алгебре: условный рисунок может быть использован для визуализации алгебраических выражений, уравнений и систем уравнений, графиков функций.
- В теории вероятностей: условный рисунок может помочь в иллюстрации вероятностных моделей, деревьев решений и графов, а также показать зависимости и взаимосвязи между случайными событиями.
- В статистике: условный рисунок может быть использован для отображения статистических данных, диаграмм и графиков, позволяя визуально анализировать и интерпретировать полученные результаты.
Применение условного рисунка в математике способствует более глубокому и понятному изучению математических концепций. Он помогает студентам улучшить свои навыки анализа, решения задач, а также развивает их воображение и креативное мышление.
Важность условного рисунка в обучении
Условный рисунок может быть использован для иллюстрации графиков, диаграмм, формул и примеров, помогая ученикам лучше понять математические концепции и применять их на практике. Он может помочь визуализировать алгоритмы, шаблоны и стратегии решения задач, что способствует развитию логического мышления и умения применять математические знания в реальных ситуациях.
Кроме того, условный рисунок может помочь ученикам лучше запомнить и организовать информацию. Визуальные образы могут быть более запоминающимися, чем текстовая информация, и помогают ученикам лучше структурировать свои знания. Они могут использовать условные рисунки в качестве подсказок и напоминаний при решении задач и воспроизведении математических концепций.
Таким образом, использование условного рисунка в обучении математике имеет значительное значение. Он помогает ученикам лучше понять и применять математические концепции, развивает их логическое мышление и помогает им запоминать и организовывать информацию. Условный рисунок может быть полезным инструментом для учителей, помогая им объяснять сложные темы и облегчая обучение математике для всех учащихся.
Вопрос-ответ:
Что такое условный рисунок в математике?
Условный рисунок в математике — это графическое представление условий задачи или логических высказываний, которые помогают решить математическую задачу или доказать математическое утверждение.
Каким образом условный рисунок помогает в решении математических задач?
Условный рисунок помогает в решении математических задач, поскольку он позволяет визуализировать условия задачи и логические связи между ними. Это позволяет лучше понять задачу и найти решение, основываясь на графическом представлении.
Какие примеры можно привести для условного рисунка в математике?
Примеры условных рисунков в математике могут включать диаграммы Венна, деревья принятия решений, графики функций и другие графические представления условий задачи или логических высказываний.
В каких областях математики применяется условный рисунок?
Условный рисунок применяется в различных областях математики, включая теорию множеств, математическую логику, теорию вероятности и статистику, алгебру и геометрию. Он может быть полезен при решении задачей, доказательстве теорем и визуализации математических концепций.
Какие преимущества имеет использование условного рисунка в математике?
Использование условного рисунка в математике имеет несколько преимуществ. Во-первых, он позволяет визуализировать сложные условия задачи, что помогает лучше понять их. Во-вторых, он помогает выявить связи между условиями задачи и найти эффективное решение. В-третьих, он может быть полезным инструментом для обучения математике, поскольку помогает студентам лучше усвоить материал и развить логическое мышление.
Развитие навыков создания условных рисунков
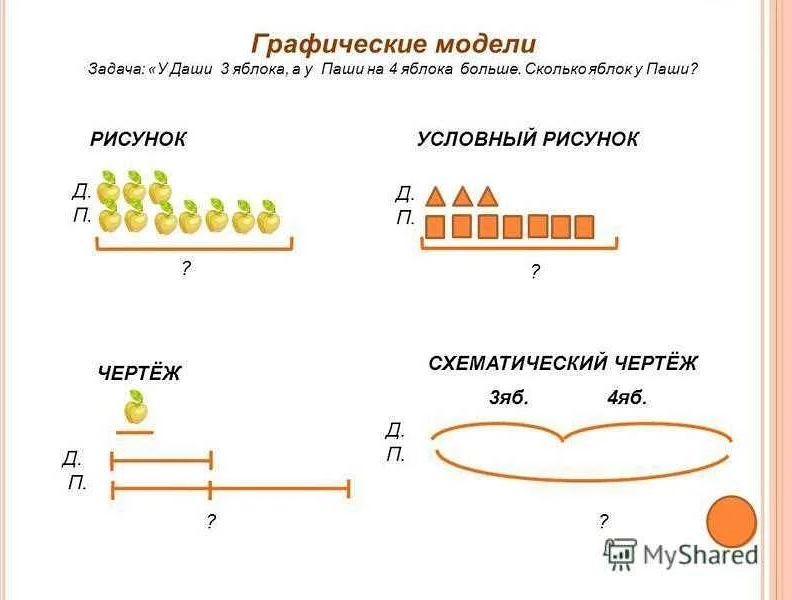
Развитие навыков создания условных рисунков начинается с понимания основных принципов и правил их построения. Это включает в себя выбор подходящих геометрических фигур и символов, а также определение логических операций и отношений.
Для развития этих навыков полезно практиковаться в создании условных рисунков на различные темы. Например, можно создать рисунок, иллюстрирующий свойства геометрических фигур или решение математических задач.
Также можно использовать условные рисунки для объяснения математических концепций или теорем. Например, можно создать рисунок, иллюстрирующий теорему Пифагора или правило сокращения дробей.
Развитие навыков создания условных рисунков помогает развить воображение и абстрактное мышление. Эти навыки могут быть полезными не только в области математики, но и в других науках и дисциплинах, где важно наглядно представить сложные концепции или отношения.


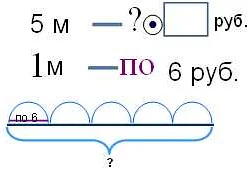
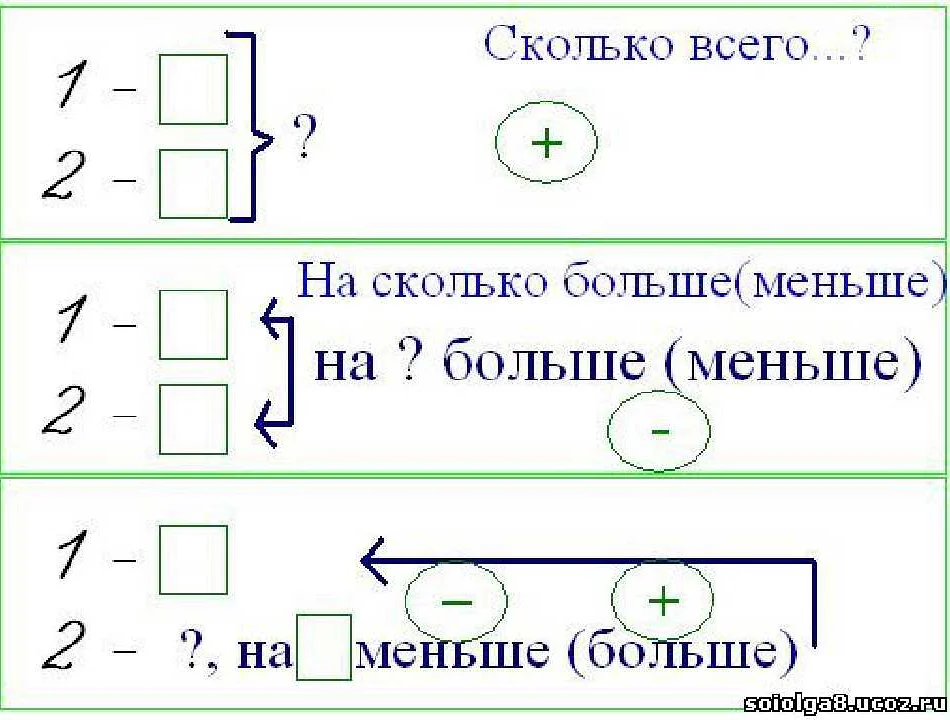

Статья очень интересная и полезная для любого, кто интересуется математикой. Я всегда думал, что математика — это только числа и формулы, но оказывается, есть еще и условные рисунки. Никогда не задумывался, что математика может быть искусством! Мне очень понравилось объяснение в статье о том, что такое условный рисунок. Это, по сути, рисунок, созданный с помощью математических функций и уравнений. Примеры, которые приведены, просто потрясающие! Не могу поверить, что такие красивые и сложные рисунки можно создать только с помощью математики. Интересно, что условные рисунки находят свое применение не только в искусстве, но и в науке. Ведь они могут помочь ученым визуализировать сложные математические концепции и модели. Это действительно удобно, ведь так гораздо проще понять и запомнить абстрактные понятия. Я думаю, что условные рисунки — это прекрасный способ развивать мышление и воображение. И хотя я сам не очень хорошо разбираюсь в математике, эта статья заинтересовала меня и заставила задуматься о том, чтобы попробовать создать свой собственный условный рисунок. Кто знает, может быть, у меня получится что-то интересное! Спасибо за такую интересную и полезную статью! Я с удовольствием прочитал ее и узнал много нового о математике. Буду ждать еще подобных статей!