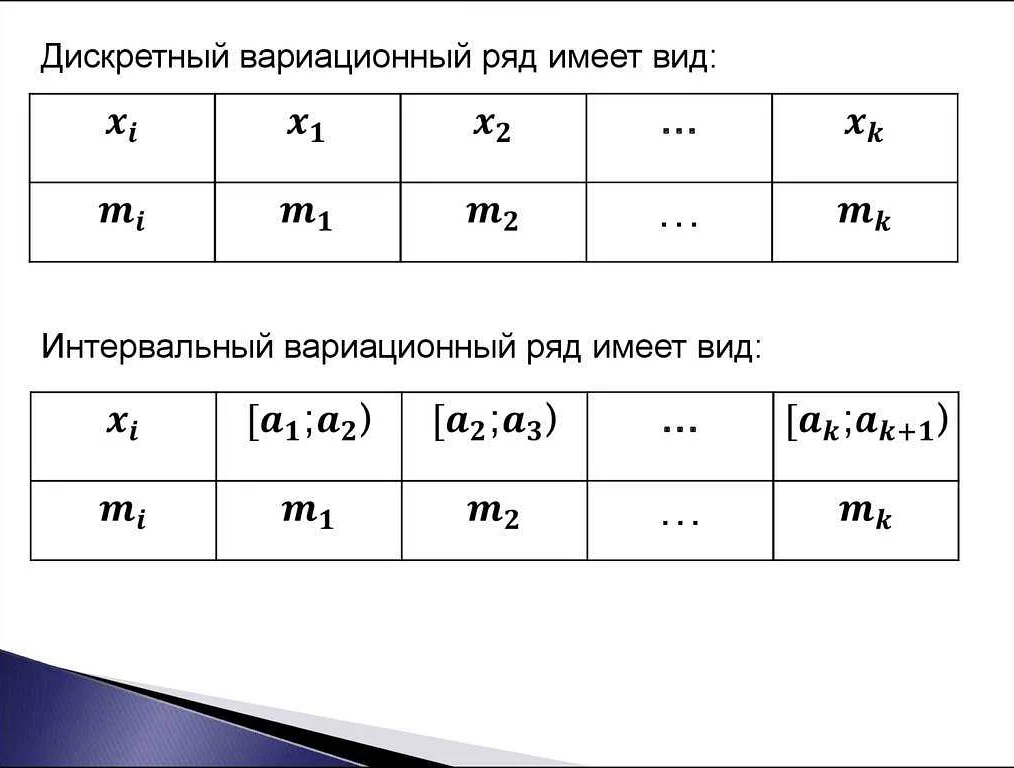
Вариационный ряд в математике: определение и примеры

Вариационный ряд в математике — это упорядоченная последовательность элементов выборки, расположенных по возрастанию. Он позволяет проводить анализ данных и находить медиану, квартили и другие характеристики распределения. Более подробно о вариационном ряде вы можете узнать из данной статьи.

Вариационный ряд является одним из базовых понятий математической статистики. Он представляет собой набор элементов выборки, упорядоченных в порядке возрастания или убывания. Определение вариационного ряда и его свойства могут быть использованы в различных областях, как в науке, так и в бизнесе и экономике.

В основном, вариационный ряд применяется для анализа распределения случайной величины и вычисления основных статистических параметров, таких как среднее значение, медиана, дисперсия и стандартное отклонение. Также вариационный ряд может быть использован для определения выбросов, т.е. значений, которые существенно отличаются от других данных в выборке.

В данной статье мы рассмотрим подробно определение вариационного ряда, приведем примеры его использования и объясним, как его применять для анализа данных в математической статистике.

Что такое вариационный ряд?

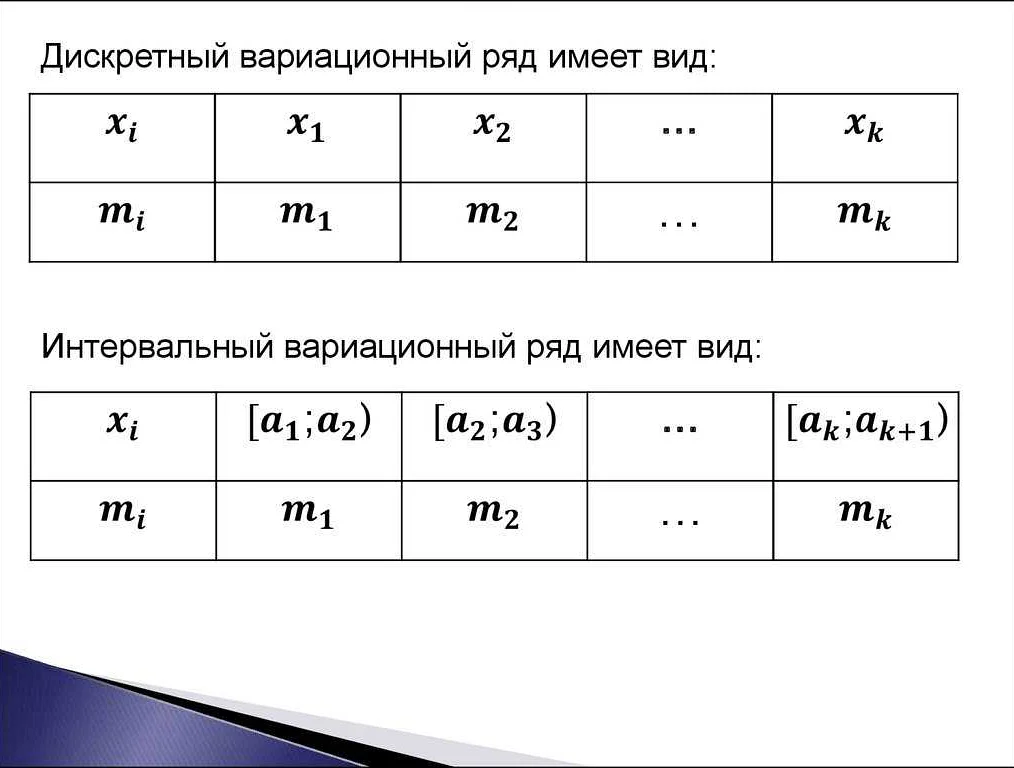
Вариационный ряд представляет собой упорядоченную последовательность измеренных значений, расположенных в порядке возрастания или убывания. Он является чрезвычайно полезным инструментом в анализе данных и статистике, позволяя оценить характер и структуру распределения величин.

Вариационный ряд может быть составлен из любого количества измерений, проведенных в различных областях, таких как экономика, наука, техника, медицина и другие. Он представляет собой информацию о том, какую линейку значений следует использовать, чтобы сделать выводы о распределении.

Каждое измеренное значение в вариационном ряде называется элементом. Элементы могут быть упорядочены в возрастающем или убывающем порядке. Например, если вы измерите длину 10 предметов, положите их в порядке от наименьшей до наибольшей длины, вы получите вариационный ряд для этой выборки.

Одним из основных преимуществ использования вариационного ряда является возможность оценки не только средней величины, но также дисперсии и стандартного отклонения выборки. Это значительно облегчает анализ и интерпретацию полученных данных.

Видео по теме:

Как составить вариационный ряд?

Вариационный ряд представляет собой последовательность элементов выборки, упорядоченных по возрастанию. Для составления вариационного ряда необходимо выполнить следующие шаги:

• Соберите выборку значений. Это могут быть любые числа или данные, которые нужно упорядочить.
• Отсортируйте выборку по возрастанию. Для этого можно использовать любой способ сортировки, например, сортировку выбором или сортировку пузырьком.
• Присвойте каждому элементу выборки свой порядковый номер в ряде. Например, первому элементу можно присвоить номер 1, второму — 2 и т.д.
• Запишите полученную последовательность элементов в порядке возрастания, указав при этом их порядковые номера. Начинайте с наименьшего элемента.

Пример составления вариационного ряда:

ВыборкаОтсортированная выборкаПорядковые номераВариационный ряд

7, 3, 5, 2, 1, 8, 4, 6

1, 2, 3, 4, 5, 6, 7, 8

1, 2, 3, 4, 5, 6, 7, 8

1, 2, 3, 4, 5, 6, 7, 8 (7, 3, 5, 2, 1, 8, 4, 6)

Вариационный ряд широко используется в статистике для анализа и интерпретации данных. Он может помочь лучше понять распределение выборки и выделить наиболее значимые значения. Кроме того, вариационный ряд может использоваться для построения гистограммы и диаграммы размаха.

Примеры вариационного ряда

Вариационный ряд – это один из наиболее важных методов статистической обработки данных. В приведенных ниже примерах мы рассмотрим несколько вариационных рядов и их применение.

1. Пример 1. Рассмотрим следующий ряд чисел: 2, 3, 5, 7, 11, 13. Для построения вариационного ряда необходимо упорядочить их по возрастанию. Получим вариационный ряд: 2, 3, 5, 7, 11, 13.
2. Пример 2. Предположим, в результате опроса изменения температуры воздуха были получены следующие данные: 23, 24, 23, 25, 21, 22, 21, 24, 25, 23, 22. Упорядочим их по возрастанию и получим следующий вариационный ряд: 21, 21, 22, 22, 23, 23, 23, 24, 24, 25, 25.
3. Пример 3. При изучении результатов тестирования по математике были получены следующие оценки: 4, 5, 2, 3, 5, 4, 3, 2, 5, 4, 2. Упорядочив их по возрастанию, получим следующий вариационный ряд: 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5.

Применение вариационного ряда может быть различным. Например, для определения среднего значения выборки, легко использовать вариационный ряд или для поиска экстремальных значений, чаще всего используются максимальное и минимальное значения вариационного ряда.

ПримерПрименение

Пример 1	Определение максимального и минимального значений вариационного ряда
Пример 2	Определение средней температуры за определенный период времени
Пример 3	Определение средней оценки теста

Как интерпретировать вариационный ряд?

Вариационный ряд – это расположение данных в порядке возрастания или убывания. Такой ряд позволяет наглядно увидеть минимальные и максимальные значения в выборке, а также определить медиану и квартили.

Минимальное значение выборки находится в начале вариационного ряда, а максимальное – в конце. Поэтому первый и последний элементы вариационного ряда могут быть использованы для определения диапазона – разности между максимальным и минимальным значением.

Медиана – это значение, которое делит выборку на две равные части. Находится медиана как середина вариационного ряда, если количество элементов нечетное, или как среднее арифметическое двух центральных элементов, если количество элементов четное.

Порядковые статистики, такие как квартили, также могут быть определены на основе вариационного ряда. Например, первый квартиль – это значение, которое разделяет выборку на четыре равные части.

Интерпретация вариационного ряда бывает полезна во многих областях, например, в статистике, экономике, физике, биологии, и т.д. Результаты анализа вариационного ряда могут помочь в принятии решений, планировании или оптимизации процессов.

Как использовать вариационный ряд в статистике?

Вариационный ряд — это упорядоченный список значений выборки по возрастанию или убыванию. В статистике вариационный ряд используется для анализа распределения данных и для выявления дисперсии в данных выборки.

С помощью вариационного ряда можно определить медиану и квартили выборки. Медиана — это значение, которое делит выборку на две равные части, а квартили — это значения, которые разделяют выборку на четыре равные части. Также, с помощью вариационного ряда можно определить экстремальные значения выборки и диапазон значений.

Вариационный ряд также используется для определения среднего значения выборки — среднего арифметического. Для этого необходимо сложить все значения выборки, а затем разделить на количество значений в выборке. Среднее значение можно использовать для оценки центра распределения данных.

Использование вариационного ряда в статистике необходимо для анализа данных выборки и для принятия решений на основе этих данных. С помощью вариационного ряда можно выявить аномалии в данных, такие как выбросы и ошибки, которые могут повлиять на результаты анализа.

Как используется вариационный ряд в экономике?

Вариационный ряд – это упорядоченный по возрастанию набор чисел. В экономике вариационный ряд может использоваться для определения различных статистических показателей, например, среднего значения или медианы.

Например, представим себе экономический индекс, который обладает различными значениями за определенный период времени. Упорядочивая эти значения вариационным рядом, мы можем легко определить среднее значение индекса за данный период или медиану, т.е. такое значение, которое делит серию на равные части.

Кроме того, вариационный ряд может быть использован для выявления аномальных значений (выбросов) в данных, что может помочь в замене или исключении этих значений для более корректного расчета статистических показателей.

Также вариационный ряд может помочь в анализе рынка и принятии решений в экономической сфере. Например, если у нас есть данные по ценам на товары, мы можем узнать, как изменяется спрос и предложение на рынке в зависимости от изменений ценовых показателей и какие цены на товары будут наиболее эффективными для максимизации прибыли.

Вариационный ряд для изучения процесса обучения

Вариационный ряд является одним из важных инструментов для изучения процесса обучения, т.к. позволяет наглядно представить изменения в успеваемости учеников. Для построения вариационного ряда необходимо упорядочить все оценки по возрастанию или убыванию, чтобы получить последовательность чисел, отражающую динамику прогресса учеников.

Вариационный ряд может использоваться как для измерения распределения оценок в классе в целом, так и для изучения конкретного ученика. Построение вариационного ряда позволяет определить такие параметры, как средняя оценка, медиана, минимальное и максимальное значение, а также размах и стандартное отклонение.

На основе данных, полученных при построении вариационного ряда, можно проводить дополнительный анализ, например, для выявления подгрупп учеников с наибольшими или наименьшими успехами. Это позволит более эффективно планировать дальнейшую работу с учениками, подстраиваясь под их индивидуальные потребности и особенности.

Таким образом, построение вариационного ряда является важным инструментом для анализа процесса обучения. Использование данного метода позволяет получить дополнительные данные о прогрессе учеников и использовать их для дальнейшего улучшения качества образования.

Применение вариационного ряда в биологии

В биологии вариационный ряд используется для анализа различных параметров, например, для изучения изменчивости признаков в популяциях живых организмов. Такие исследования позволяют установить, какие признаки наиболее изменчивы и насколько значимы эти изменения.

Одним из примеров такого исследования является анализ вариационного ряда роста растительных особей. С помощью вариационного ряда можно определить диапазон изменчивости роста и выделить особи, которые превышают средний уровень. Это помогает выяснить, какие особи являются самыми высокими и наиболее пригодными для дальнейшего использования в селекции.

Также вариационный ряд используется при исследовании мутационных процессов в популяциях. Изучая вариационный ряд мутаций, можно определить их частоту и выявить, какие из мутаций более или менее значимы для вида. Это помогает прогнозировать развитие мутационных процессов и понимать, как они могут влиять на выживаемость и популяционную динамику вида.

Итак, вариационный ряд в биологии играет важную роль при изучении различных параметров живых организмов. Он позволяет анализировать изменчивость признаков и определять их значимость для видовой и генетической изменчивости. Это может быть полезно для селекционных работ и понимания мутационных процессов в популяциях.

Вариационный ряд в химии

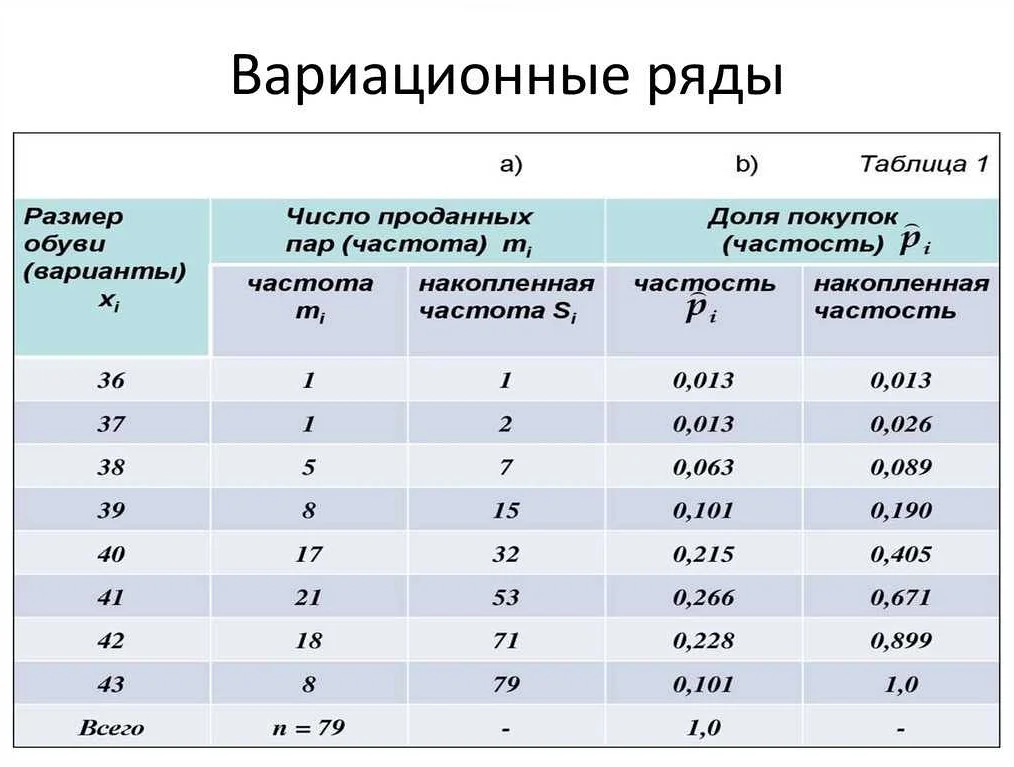
В химии вариационный ряд используется для упорядочивания химических соединений по их свойствам. Это позволяет проводить сравнение между различными соединениями с целью выявления закономерностей в их свойствах и поведении.

Для составления вариационного ряда в химии можно выбрать различные свойства соединений, такие как плотность, температура кипения, растворимость, активность и т.д. Вариационный ряд обычно представляется в виде таблицы или списка, в котором соединения упорядочиваются по возрастанию или убыванию выбранного свойства.

Вариационный ряд в химии может иметь различные применения, например, он может использоваться для определения наиболее эффективных химических соединений для определенных процессов, для проведения сравнительных исследований между различными соединениями и для выявления закономерностей и трендов в свойствах химических соединений.

Помимо этого, вариационный ряд может быть полезен для обучения студентов химии, позволяя им более глубоко понимать химические свойства и взаимодействия между соединениями.

В целом, вариационный ряд является важным инструментом в химии, который позволяет систематизировать и анализировать свойства химических соединений.

Вариационный ряд в физике

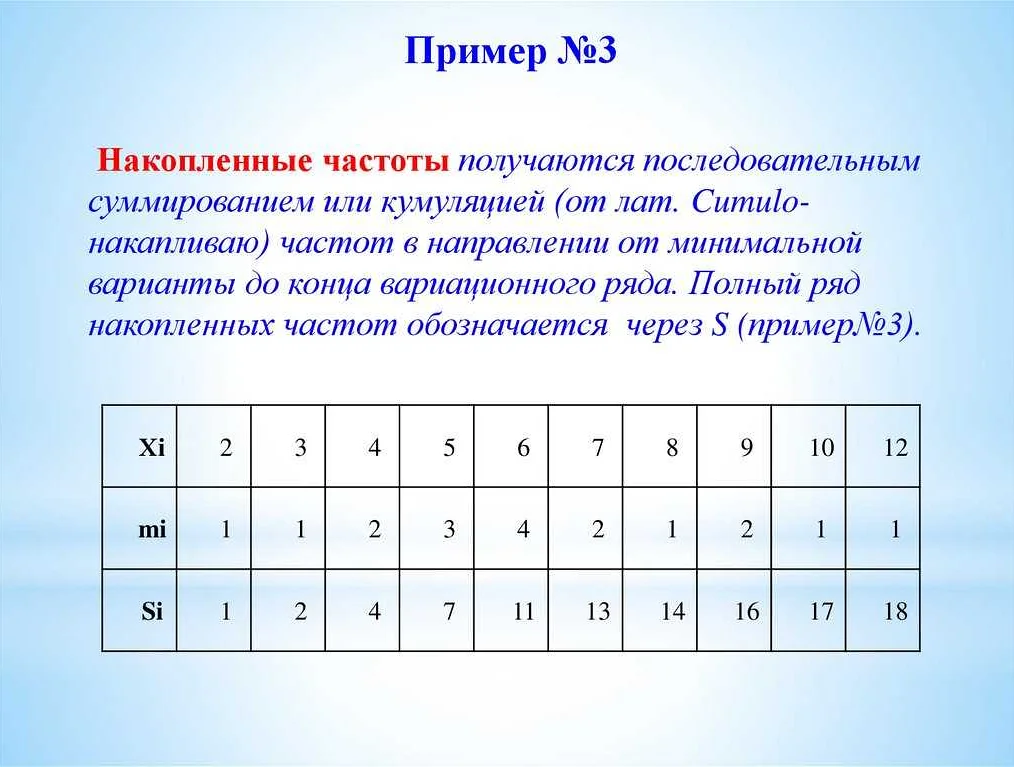
Вариационный ряд — это упорядоченный набор чисел, рассчитанный в результате измерений. Этот метод широко используется в физике для определения наилучшего приближения к исследуемой величине.

Применение метода вариационного ряда в физике позволяет получить точные результаты и снизить вероятность ошибок. Например, при измерении физической величины с помощью приборов, возможны случайные отклонения от реального значения. С помощью вариационного ряда можно уменьшить влияние этих ошибок и получить более точный результат.

Вариационный ряд в физике строится на основе статистических данных, полученных в ходе экспериментов. Для этого сначала проводятся несколько измерений и записываются результаты. Затем эти результаты упорядочиваются по возрастанию или убыванию и строится вариационный ряд. Он показывает все полученные значения и позволяет определить наиболее вероятное значение исследуемой величины.

Вариационный ряд является важным инструментом для проведения научных исследований в физике и других областях науки. Он позволяет упорядочить и анализировать данные, полученные в результате измерений, и получать более точные результаты экспериментов.

Выводы

1. Вариационный ряд – это упорядоченный по возрастанию или убыванию ряд, составленный из выборочных данных. Вариационный ряд имеет много применений в статистике и математике. С помощью вариационного ряда можно узнать основные статистические показатели, такие как медиана, дисперсия, квантили, среднее значение и т.д.

2. Вариационный ряд помогает оценить свойства выборки. Он позволяет увидеть, как распределены данные в выборке, насколько они различаются друг от друга, а также оценить вероятность получения конкретного значения.

3. Используя вариационный ряд, можно производить сравнение различных выборок. Также можно сравнивать множество выборок по нескольким параметрам, таким как среднее значение и стандартное отклонение.

4. Вариационный ряд можно использовать для определения выбросов. Выбросы – это значения, выходящие за пределы обычного диапазона значений в выборке. Их можно обнаружить, отсортировав данные вариационного ряда и посмотрев, какие значения находятся далеко от медианы.

5. Вариационный ряд может быть использован для анализа временных рядов. Это позволяет выявить изменения в данных в течение времени и сделать прогнозы на будущее.

Вариационный ряд – это важный инструмент для анализа статистических данных. Он может помочь оценить свойства выборки, сравнить различные выборки, определить выбросы, а также использоваться для анализа временных рядов.

Вопрос-ответ:

Что такое вариационный ряд?

Вариационный ряд — это ряд, который состоит из всех элементов выборки, упорядоченных по возрастанию (или убыванию). Этот ряд позволяет проанализировать наибольшее и наименьшее значение в выборке, а также рассчитать различные статистические показатели, такие как дисперсия, медиана и процентили.

Какую роль играет вариационный ряд в статистике?

Вариационный ряд является важным инструментом в статистике, поскольку он позволяет рассчитать различные показатели, такие как дисперсия и медиана. Благодаря вариационному ряду можно определить, каков разброс значений выборки, а также найти минимальное и максимальное значение в выборке. Эти данные могут быть полезными при принятии решений на основе статистических данных.

Как правильно упорядочить элементы выборки в вариационном ряду?

Элементы выборки в вариационном ряду следует упорядочить по возрастанию или убыванию. Если значения повторяются, то их нужно группировать вместе. Например, если выборка содержит числа 1, 2, 3, 3, 4, 5, то вариационный ряд будет выглядеть так: 1, 2, 3(2), 4, 5. Группировка повторяющихся значений позволяет сократить количество элементов в ряду и упрощает дальнейший анализ данных.

Как рассчитать медиану с помощью вариационного ряда?

Для рассчета медианы необходимо найти середину вариационного ряда. Если количество элементов в выборке нечетное, то медиана будет являться средним значением. Например, если выборка состоит из чисел 1, 2, 3, 4, 5, то медиана будет равна 3. Если количество элементов четное, то медиана будет находиться между двумя средними значениями. В этом случае нужно найти среднее значение двух чисел, стоящих в середине выборки. Например, если выборка состоит из чисел 1, 2, 3, 4, то медиана будет равна (2 + 3) / 2 = 2,5.

Как рассчитать дисперсию с помощью вариационного ряда?

Для рассчета дисперсии необходимо вычислить среднее арифметическое значения выборки и вычислить разницу каждого элемента выборки с этим средним значением. Затем нужно возвести полученные значения в квадрат, сложить их и поделить на количество элементов выборки. Например, если выборка состоит из чисел 1, 2, 3, 4, 5, то среднее значение равно (1+2+3+4+5)/5 = 3. Далее нужно вычислить отклонение каждого элемента выборки: (-2, -1, 0, 1, 2). Возводим их в квадрат: (4, 1, 0, 1, 4). Складываем: 4+1+0+1+4 = 10. И делим на количество элементов выборки: 10/5 = 2 — это и будет дисперсия.

Как можно использовать вариационный ряд для определения выбросов?

Вариационный ряд позволяет определить наибольшее и наименьшее значение в выборке, что может помочь в выявлении выбросов. Выбросы — это значения, которые кардинально отличаются от остальных элементов выборки и могут быть результатом ошибок в измерении, некоторых редких явлений или просто некорректных данных. Чтобы определить выбросы с помощью вариационного ряда, можно использовать метод трех сигм. Можно рассчитать среднее значение и стандартное отклонение выборки, умножить его на три и вычислить пределы вариационного ряда. Значения, которые выходят за эти пределы, могут быть отнесены к выбросам.

Как вариационный ряд используется в деловой сфере?

Вариационный ряд может быть полезен в различных сферах, включая деловую сферу. Например, при анализе финансовых показателей компании, вариационный ряд может помочь выявить тенденции роста или падения, а также определить наибольшее и наименьшее значение показателей. Это может помочь при принятии решений о будущих инвестициях или планировании бюджета. Вариационный ряд также может использоваться при анализе рынка, что позволяет выявить наиболее востребованные товары и услуги, отследить ценовые тенденции и прогнозировать изменения в отрасли.