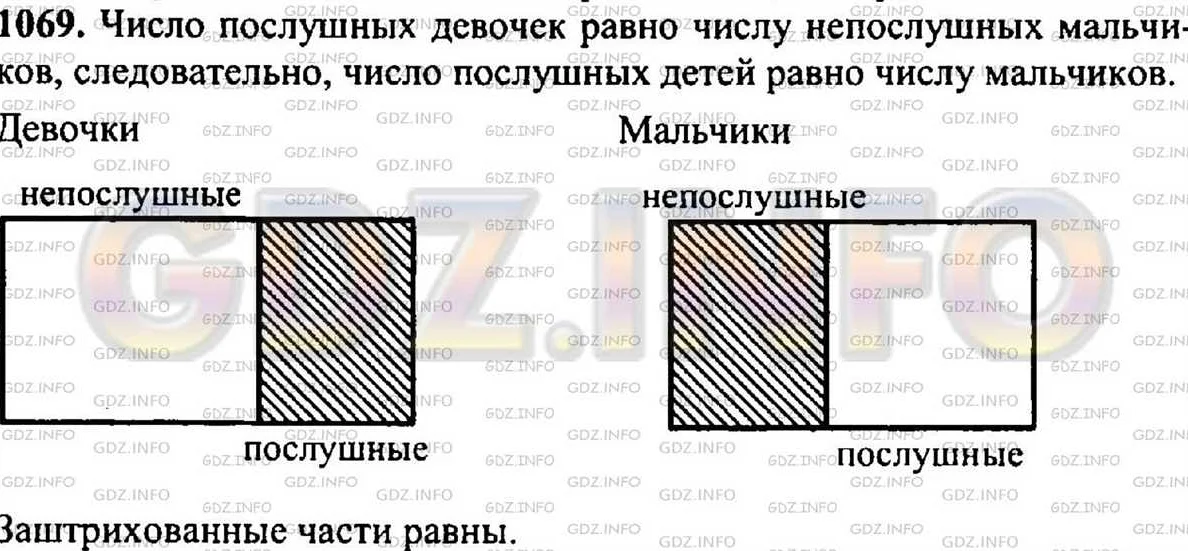
Какова вероятность того, что в семье с двумя детьми оба ребенка будут мальчиками?

Статья ответит на вопрос о вероятности рождения двух мальчиков в семье с двумя детьми. Подробное объяснение и формулы расчета дадут понимание теории вероятности и ее применения в жизни.

Эта тема вызывает много дискуссий, вопросов и неоднозначных мнений. Возможность того, что оба детей в семье — мальчики, является одним из наиболее интересных приложений вероятностной теории в жизни.

В данной статье мы рассмотрим теорию вероятности на примере семьи, в которой два ребенка. Мы выясним, какова вероятность того, что оба детей будут мальчиками, если известно, что хотя бы один из них мальчик. Мы также рассмотрим несколько примеров и попытаемся вывести правило, на основании которого можно было бы определить вероятность такой ситуации.

Внимание! Предупреждаем, что данный материал может содержать математические выкладки и формулы. Если вы не знакомы с теорией вероятности, рекомендуется внимательно прочитать статью и сначала изучить основы данной теории.

Вероятность рождения мальчика или девочки

Вся жизнь человека начинается с момента рождения, когда становится известным пол младенца. Вероятность рождения мальчика или девочки в обществе почти равна, но наши представления о бинарных гендерах делают этот выбор более важным для многих людей.

Гендерное разделение уже стартует на этапе беременности, где врачи могут дать примерное представление о том, какой пол будет у младенца. Однако, получить полное понимание не удастся до тех пор, пока не пройдет время рождения.

Относительно вероятности, что младенец будет мальчиком или девочкой, сейчас в мире рождается примерно одинаковое количество мальчиков и девочек. Но в отдельных случаях, на эту вероятность может влиять много факторов, таких как генетические особенности или методы стимуляции рождения.

В то время как у каждой пары есть вероятность родить ребенка мальчика или девочку, каждый ребенок все же уникален и имеет свои индивидуальные характеристики. Поэтому не следует поддаваться стереотипам или гендерным ожиданиям, а просто любить и заботиться о своем ребенке, независимо от его пола.

Два ребенка в семье

Множество семей по всему миру имеют двух детей. Интересно, что многие родители задаются вопросом: «Какова вероятность того, что у нас два мальчика?» или «Какова вероятность того, что один мальчик и одна девочка?». С этими вопросами связана теория вероятностей, которая очень полезна в математике, экономике и науке в целом.

Известно, что вероятность рождения мальчика и девочки приблизительно одинакова. Таким образом, в семье с двумя детьми есть четыре возможных комбинации пола: два мальчика, две девочки, мальчик и девочка в разном порядке. Следовательно, вероятность того, что у семьи с двумя детьми будут два мальчика, составляет 1/4 или 25%.

Важно отметить, что вероятность не зависит от того, какой пол у первого ребенка. То есть, если первый ребенок — мальчик, вероятность рождения второго мальчика все равно составит 1/4.

Таким образом, можно говорить о более общем законе — законе умножения в теории вероятности. Согласно этому закону, вероятность двух независимых событий произойти друг за другом, равна произведению вероятности каждого события. В нашем случае, первое рождение является независимым событием, и, следовательно, вероятность рождения второго мальчика равна 1/2 (как и вероятность рождения первого мальчика). В результате, общая вероятность того, что в семье с двумя детьми будут два мальчика, составляет 1/2 x 1/2 = 1/4 или 25%.

Таким образом, можно утверждать, что вероятность рождения двух мальчиков в семье с двумя детьми составляет 25%, и она не зависит от пола первого ребенка или других факторов.

Вероятность того, что первый ребенок мальчик

Исследование вероятности наличия двух мальчиков в семье с двумя детьми часто ведется по двум критериям. Один из них — вероятность того, что первый ребенок является мальчиком. Эта вероятность равна 1/2, так как у каждого ребенка равные шансы быть мальчиком или девочкой.

Эта вероятность не меняется от того, является ли второй ребенок мальчиком, девочкой или старшим по возрасту. То есть, если знать информацию только о первом ребенке, то вероятность того, что в семье с двумя детьми есть два мальчика, будет равна вероятности того, что оба детей являются мальчиками — 1/4.

Этот критерий не может использоваться для определения вероятности наличия двух мальчиков в семье с тремя или более детьми. В этом случае необходимо использовать другие методы статистического анализа.

Вероятность того, что второй ребенок мальчик

При рассмотрении темы о вероятности мальчика или девочки в семье с двумя детьми, важным вопросом является вероятность того, что второй ребенок мальчик. Для расчета данной вероятности можно использовать принцип условной вероятности.

Предположим, что вероятность рождения мальчика или девочки равна 0,5. В этом случае, вероятность того, что у семьи с двумя детьми будут оба мальчика, составляет 0,25 (0,5 * 0,5). Однако, если известно, что старший ребенок является мальчиком, то вероятность того, что у семьи двое мальчиков, увеличивается. Это связано с тем, что младший ребенок может быть мальчиком или девочкой, а вероятность рождения каждого пола равна 0,5.

Таким образом, используя принцип условной вероятности, можно рассчитать, что вероятность того, что второй ребенок мальчик, при условии, что старший — мальчик, равна 0,5.

Это означает, что если вам известно, что у семьи с двумя детьми старший ребенок — мальчик, то шансы того, что второй ребенок также мальчик, равны 50 процентам. Однако, следует учитывать, что это относится только к конкретной ситуации и не является общей вероятностью рождения мальчика в семье с двумя детьми.

В общем случае, вероятность того, что второй ребенок мальчик, составляет 0,5, так как пол каждого ребенка определяется независимо от пола другого ребенка.

Вероятность того, что оба ребенка мальчики

Задача о вероятности того, что в семье с двумя детьми оба ребенка мальчики, является классическим примером теории вероятностей. На первый взгляд кажется, что вероятность этого равна 1/2, так как ребенок может быть мальчиком или девочкой с равной вероятностью. Но это не совсем верно.

Чтобы решить эту задачу, необходимо использовать комбинаторику. В семье с двумя детьми может быть четыре возможных исхода: мальчик-мальчик, мальчик-девочка, девочка-мальчик и девочка-девочка. Из них только один исход соответствует условию, что в семье оба ребенка мальчики.

Следовательно, вероятность того, что в семье с двумя детьми оба ребенка мальчики, равна 1/4. Важно отметить, что эта вероятность не зависит от того, какой пол у первого ребенка, так как вероятность рождения мальчика и девочки в каждой своей ситуации одинакова.

Таким образом, вероятность того, что в семье с двумя детьми оба ребенка мальчики, может показаться неожиданно низкой, но она корректно определяется при использовании комбинаторных методов.

Полная вероятность и условная вероятность

Полная вероятность заключается в том, что сумма вероятностей всех исходов данного события равна 1. Если мы имеем несколько взаимоисключающих событий, то вероятность каждого из них можно получить путем умножения вероятности на условную вероятность этого события при допущении верности других взаимоисключающих событий. Для расчета полной вероятности используют формулу умножения, a если переменных более двух, тогда вычислить вероятность каждого значения при одновременном наступлении всех событий можно с помощью формулы произведения.

• Пример 1: Вероятность выпадения орла или решки при бросании монеты равна 1, так как они являются неисключающими исходами.
• Пример 2: Вероятность того, что в семье с двумя детьми оба мальчики, равна 1/4, так как существует четыре возможных исхода: MM, MF, FM, FF, и только один из них соответствует обоим мальчикам.
• Пример 3: Пусть у нас есть два мешка с шариками, первый содержит 3 черных и 2 красных шарика, а второй — 2 черных и 4 красных шарика. Мы выбираем один из мешков наугад, и затем выбираем шарик из него случайным образом. Если мы хотим вычислить вероятность того, что мы выберем красный шарик, то мы можем использовать формулу полной вероятности: P(R) = P(M1)P(R|M1) + P(M2)P(R|M2), где P(M1) = 1/2 — вероятность выбора первого мешка, P(M2) = 1/2 — вероятность выбора второго мешка, P(R|M1) = 2/5 — вероятность выбора красного шарика из первого мешка, P(R|M2) = 2/3 — вероятность выбора красного шарика из второго мешка. Таким образом, P(R) = (1/2)*(2/5) + (1/2)*(2/3) = 11/30.

Условная вероятность подразумевает вероятность наступления одного события при условии наступления другого события. Если P(A) и P(B) не равны нулю, тогда вероятность наступления события A при условии наступления события B может быть определена следующим образом: P(A|B) = P(A∩B)/P(B). Когда A и B — независимые события, то вероятность наступления A равна вероятности наступления события B.

1. Пример 1: Вероятность выпадения головы при бросании монеты, при условии, что монета падет на это. P(A|B) = 1/2, так как вероятность того, что монета выпадет на голову, равна 1/2, и эта вероятность не зависит от того, как монета была брошена.
2. Пример 2: Вероятность того, что в семье с двумя детьми оба дети будут мальчиками, при условии, что в семье есть хотя бы один мальчик. P(AB|A) = P(AB)/P(A) = (1/4)/(1/2) = 1/2, так как только два из четырех возможных исходов соответствуют семьям с хотя бы одним мальчиком (MM, FM), а исключены варианты, когда в семье две девочки (FF).
3. Пример 3: Пусть у нас есть два мешка с шариками, первый содержит 3 черных и 2 красных шарика, а второй — 2 черных и 4 красных шарика. Мы выбираем один из мешков наугад, и затем выбираем шарик из него случайным образом. Если мы хотим вычислить вероятность выбора красного шарика из первого мешка, при условии, что мы выбрали первый мешок, то мы можем использовать формулу условной вероятности: P(R1|M1) = P(R1∩M1)/P(M1) = (2/5)*(1/2) / (3/5) = 1/3, где P(R1∩M1) — вероятность того, что мы выберем красный шарик из первого мешка, P(M1) = 1/2 вероятность выбора первого мешка.

Формула Байеса

Формула Байеса – это математический алгоритм для вычисления вероятности того, что событие А произошло, при условии наступления события B.

Формула Байеса основана на теории условной вероятности, а также на теореме умножения и теореме сложения вероятностей. Формула очень важна в статистике, медицине, экономике и других областях.

Применение формулы Байеса на примере семьи с двумя детьми позволяет определить, какова вероятность того, что оба ребенка будут мальчиками, если известно, что есть хотя бы один мальчик.

В случае с двумя детьми возможны четыре варианта: два мальчика, две девочки, старший мальчик и младший мальчик, старшая девочка и младший мальчик. При этом условие «есть хотя бы один мальчик» убирает возможность второго варианта, и мы смотрим только на три возможных варианта.

Вероятность того, что оба ребенка мальчики, составляет 1/3 по формуле Байеса. Для этого необходимо знать вероятность того, что оба дети могут быть мальчиками (1/4) и условную вероятность того, что оба дети мужского пола, при условии, что есть хотя бы один мальчик (1/3).

Дерево вероятностей

Вероятность событий можно изобразить графически при помощи дерева вероятностей. Для нашей задачи «Вероятность того, что в семье с двумя детьми оба мальчики» мы можем построить такое дерево.

Первое ребро дерева соответствует рождению первого ребенка. Вероятность рождения мальчика или девочки равна 1/2. Далее, для каждого из этих случаев, проводятся две ветви дерева, соответствующие рождению второго ребенка. Так, у нас может быть четыре возможных исхода: мальчик-мальчик, мальчик-девочка, девочка-мальчик, девочка-девочка.

В нашем случае нас интересует вероятность исхода «мальчик-мальчик». Она будет равна 1/2 * 1/2 = 1/4 или 0.25.

Таким образом, дерево вероятностей может быть очень удобным инструментом для визуального представления вероятностей различных событий.

Вероятность для разных комбинаций пола детей

Пусть семья имеет двух детей. Возможны следующие комбинации пола детей:

• Обе девочки
• Один мальчик и одна девочка
• Оба мальчика

Согласно законам вероятности, вероятность каждой из комбинаций равна 1/2 * 1/2, или 1/4. То есть каждая из этих комбинаций имеет вероятность 25%.

Однако, если мы знаем, что в семье уже есть один мальчик, то вероятность того, что второй ребенок будет мальчиком, составляет 1/2. Таким образом, вероятность того, что оба детей будут мальчиками, равна 1/2 * 1/2, или 1/4, что составляет 25%.

Интересно отметить, что даже если мы знаем, что в семье есть один мальчик, это не означает, что вероятность рождения второго мальчика увеличивается. В любом случае вероятность того, что второй ребенок будет мальчиком, составляет 1/2.

Вероятность для разных комбинаций пола детейКомбинация половВероятность

Обе девочки	1/4 (25%)
Один мальчик и одна девочка	1/4 (25%)
Оба мальчика	1/4 (25%)

В заключение стоит отметить, что вероятность того, что в семье с двумя детьми оба мальчики, равна 1/4, или 25%. Никакие другие факторы, кроме пола первого ребенка, не влияют на эту вероятность.

Влияние порядка рождения на вероятность

Вероятность того, что пара родителей имеет двух мальчиков или двух девочек равна 25%. Однако, если известен порядок рождения детей, то вероятность может измениться.

Рассмотрим ситуацию, когда первым ребенком является мальчик. В этом случае вероятность рождения второго мальчика составляет 50%, так как рождение второго ребенка не зависит от пола первого ребенка. Следовательно, вероятность того, что в такой семье будут два мальчика, составляет 25% (0,5 * 0,5).

Если же первым ребенком является девочка, то вероятность рождения второй девочки также составляет 50%. Но в этом случае вероятность рождения двух мальчиков будет равна 0%, так как уже родилась девочка. Следовательно, вероятность того, что в такой семье будут две девочки, также составляет 25% (0,5 * 0,5).

Из этих примеров видно, что порядок рождения детей может влиять на вероятность того, что в семье будут два мальчика или две девочки. Но если учитывать все возможные комбинации, то вероятность рождения такой пары детей всегда будет равна 25%.

Отличия между теоретической и эмпирической вероятностью

Теоретическая вероятность — вероятность наступления определенного события, которая рассчитывается на основе теоретических знаний и формул. Она является идеальной вероятностью и представляет математическую модель, описывающую вероятность наступления событий.

Например, если бросить монету, то теоретическая вероятность выпадения орла равна 0,5, так как существует два равновероятных исхода: выпадение орла или решки.

Эмпирическая вероятность — вероятность наступления определенного события, которая определяется на основе статистических данных и экспериментов. Она является результатом реальных наблюдений и обычно используется для проверки теории.

Например, если бросить монету 100 раз и орел выпадет 60 раз, то эмпирическая вероятность выпадения орла равна 0,6. Эта вероятность может отличаться от теоретической вероятности, так как она основана на конкретных результатах наблюдений и экспериментов.

Отличия между теоретической и эмпирической вероятностью заключаются в том, что теоретическая вероятность является математической моделью, которая предполагает равновероятность всех исходов, а эмпирическая вероятность основана на конкретных данных и наблюдениях, которые могут отличаться от теоретических расчетов. Теоретическая вероятность может использоваться для предсказания вероятности наступления события, а эмпирическая вероятность может использоваться для проверки теоретических расчетов и уточнения вероятности на основе реальных наблюдений.

Вопрос-ответ:

Каковы шансы, что в семье с двумя детьми будут две дочери?

Вероятность того, что в семье будут две дочери, составляет 1/4 или 25%. Это происходит, когда оба ребенка девочки. Так как события рождения мальчиков и девочек независимы, вероятность любой из этих ситуаций составляет 1/2, то есть 50%.

А если один ребенок мальчик, то какова вероятность, что второй ребенок также мальчик?

Если один ребенок мальчик, то существует две возможные ситуации: первый ребенок мальчик и второй ребенок девочка, или оба ребенка мальчики. Вероятность того, что оба ребенка будут мальчики, составляет 1/2 или 50%, так как второй ребенок может быть как мальчиком, так и девочкой.

А если старший ребенок мальчик, то каковы шансы, что второй ребенок тоже мальчик?

Если старший ребенок мальчик, то это не влияет на вероятность того, что второй ребенок будет мальчиком. Все еще есть две возможные ситуации: оба ребенка мальчики или один мальчик и одна девочка. Вероятность того, что второй ребенок будет мальчиком все так же составляет 1/2 или 50%.

А есть ли вероятность того, что в семье с двумя детьми будет ровно один мальчик?

Да, вероятность того, что в семье с двумя детьми будет ровно один мальчик, также составляет 1/2 или 50%. Это может произойти в ситуации, когда первый ребенок — мальчик, а второй – девочка или, наоборот, первый ребенок – девочка, а второй – мальчик.

А если известно, что старший ребенок мальчик, то каковы шансы, что второй ребенок девочка?

Если известно, что старший ребенок мальчик, то это не влияет на вероятность того, что второй ребенок будет девочкой. Вероятность того, что второй ребенок будет девочкой, также составляет 1/2 или 50%, так как события рождения мальчика и рождения девочки независимы друг от друга.

А какие все возможные комбинации полов детей могут быть в семье с двумя детьми?

В семье с двумя детьми могут быть четыре возможные комбинации полов: двух мальчиков, двух девочек, мальчика и девочки в любом порядке. Комбинация «мальчик-девочка» включает в себя две разные комбинации – «старший мальчик, младшая девочка» и «младший мальчик, старшая девочка».

А почему вероятность того, что в семье с двумя детьми оба мальчики, такая же, как и вероятность того, что оба детей будут девочками?

Вероятность того, что оба детей будут мальчиками или оба будут девочками, одинакова потому что они оба являются примерами «успешных» исходов, то есть исходов, при которых оба ребенка будут иметь одинаковый пол. Каждому исходу соответствует вероятность, и так как сумма вероятностей всех возможных исходов должна быть равна 1, вероятность того, что оба детей будут мальчиками или оба будут девочками составляет 1/4 или 25%.

Видео по теме: