Выражение в математике для 1 класса: как правильно понять и объяснить?

Выражение в математике для 1 класса — это математическое выражение, которое учит детей считать и решать простые задачи, помогая им развивать логическое мышление и математические навыки. Узнайте больше о выражениях в математике для первоклашек.

Математика – это один из самых важных предметов в школе, и чем раньше дети научатся ее понимать, тем лучше. Уже в начальной школе дети начинают изучать основные математические понятия, такие как числа, операции и выражения. И понимание того, что такое выражение, является ключевым шагом в обучении математике изучающих ее учеников первого класса.

Выражение в математике – это математическое уравнение, которое состоит из чисел, операций и переменных. Такие уравнения построены таким образом, чтобы можно было вычислить их значение при определенных условиях. Простейшим примером выражения может быть операция сложения двух чисел, например, 2 + 3. Это выражение можно рассматривать как уравнение, которое можно решить и получить конечный результат.

Изучение выражений в математике первого класса – это первый шаг на пути к обучению в этой области. Ученики должны начать с понимания основных математических операций и постепенно двигаться к более сложным выражениям. Хорошее понимание выражений поможет детям лучше понимать составляющие математических уравнений, и таким образом, основы математики станут более доступными и интересными.

Выражение в математике для 1 класса: что это

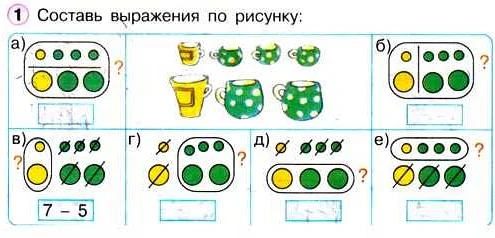
Выражение в математике для 1 класса — это математическое выражение, которое содержит числа, знаки операций и переменные. Это может быть выражение типа 2+3 или 4-1, но также может быть более сложным, например 2(3+1) или 5-2+1.

Выражения в математике помогают решать различные задачи и рассчитывать математические значения. Важно учить детей составлять выражения и правильно решать задачи, используя математические выражения. Различные математические операции, такие как сложение, вычитание и умножение, можно использовать в выражениях.

Для изучения выражений в математике для 1 класса необходимо узнать базовые математические операции и их правила. Это поможет понимать, как работать с числами и как решать простые математические задачи. Детям рекомендуется тренироваться в составлении выражений и решении простых математических задач, чтобы улучшить свои навыки и подготовиться к более сложным задачам в будущем.

Изучение выражений в математике должно начинаться с самых простых примеров и постепенно переходить к более сложным задачам и выражениям. Детям нужно помогать в изучении правил математических операций, чтобы они могли понимать, как работают эти операции и как применять их в решении задач.

Видео по теме:

Определение

Выражение в математике — это сочетание цифр, знаков математических операций и переменных, записанных в определенном порядке.

Для детей первого класса изучение выражений начинается с основных математических операций — сложения и вычитания. Эти операции дети встречают в жизни ежедневно: складывая конфеты, вычитая жетоны на играх и т.д.

Поэтому в начальной школе особое внимание уделяется формированию начальных математических представлений.

Изучение выражений в математике помогает детям развивать математический мышление, логическое мышление и умение работать с числами.

Примеры

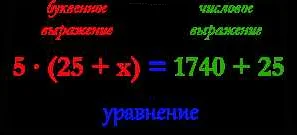
Примеры выражений в математике для 1 класса:

• 2 + 3
• 4 — 1
• 7 — 3
• 5 + 0

Все эти выражения можно вычислить с помощью основных арифметических операций: сложения и вычитания. Эти примеры помогут детям понять, как работать с числами и изучать математику.

Еще примеры выражений:

1. 8 + 2 — 6
2. 5 + 4 — 3
3. 12 — 6 + 3

Эти выражения уже сложнее, так как в них есть несколько арифметических операций. Однако они также легко вычисляемы и помогут детям улучшить свои навыки в математике.

Таблица с выражениями в математике для 1 классаВыражениеОтвет

4 + 2	6
9 — 5	4
7 + 1 — 2	6

Таблица также предоставляет примеры выражений в математике для 1 класса. Они просты в вычислении, но помогут детям тренироваться в использовании арифметических операций.

Изучение выражений в математике для 1 класса

Изучение выражений – это важная часть математического образования для учеников первого класса. В рамках этого предмета, дети учатся создавать и решать простейшие математические формулы.

При изучении выражений ученики учатся определять операции, такие как сложение, вычитание, умножение и деление. Они также учатся работать с числами, чтобы создавать простые математические уравнения.

Ученики учатся различать математические символы, такие как знаки плюс, минус, умножить и разделить. Они также учатся понимать, как использовать эти символы вместе с числами, чтобы создавать математические формулы.

Изучение выражений является важным шагом в развитии математической грамотности у учеников первого класса. Этот предмет помогает детям освоить основы математики и подготовиться к изучению более сложных математических концепций в будущем.

Раскрытие скобок

Раскрытие скобок – это одна из основных операций в алгебре. Оно состоит в том, чтобы выполнить умножение между скобками и элементами, которые находятся за скобками. Раскрытие скобок используется во многих задачах по алгебре и арифметике.

В 1 классе дети начинают изучать основы арифметики, включая скобки. Раскрытие скобок обычно не изучается в этом классе, поскольку дети еще не знакомы с понятием переменных. Однако, учитель может использовать конкретные примеры с числами и знаком «плюс» или «минус», чтобы помочь детям лучше понять, как работать со скобками.

Например, рассмотрим пример: (2 + 3) + 4. Для раскрытия скобок нам нужно сначала сложить 2 и 3, а затем выполнить умножение между результатом и 4. Таким образом, мы получим: 5 + 4 = 9.

Раскрытие скобок может быть сложно для некоторых студентов, поэтому важно повторять понятие многократно и приводить кучу примеров. Следует также помнить, что раскрытие скобок – это только одна из многих операций, которые дети будут изучать в будущем, поэтому важно понимать, как оно работает и как оно включается в работу более сложных математических примеров.

Приоритет операций

При решении математических задач необходимо знать приоритет операций, то есть порядок, в котором нужно выполнять действия.

В первую очередь нужно делать действия в скобках. Если скобок несколько, сначала решаем самые внутренние, затем те, которые находятся снаружи и так далее.

Далее выполняются вычисления, связанные с умножением и делением. Они имеют одинаковый приоритет и выполняются слева направо. Например, в выражении 2 + 3 * 4 сначала нужно выполнить умножение, а только потом сложение: 2 + 12 = 14.

Последними выполняются действия, связанные с сложением и вычитанием. Они также имеют одинаковый приоритет и выполняются слева направо. Например, в выражении 6 — 2 + 1 сначала нужно вычесть 2 из 6, а затем прибавить 1: 6 — 2 + 1 = 5.

Знание приоритета операций поможет правильно решать математические задачи и избежать ошибок в вычислениях.

Выражения с целыми числами

Выражение в математике — это математическое выражение, состоящее из чисел, переменных, знаков операций и скобок. В выражениях с целыми числами к числам можно относить целые числа, положительные и отрицательные.

Как правило, выражения с целыми числами используются для решения математических задач. Например, для выполнения арифметических операций или составления алгебраических уравнений.

Чтобы успешно изучать выражения с целыми числами, нужно уметь выполнять основные арифметические действия (сложение, вычитание, умножение, деление) и использовать правила порядка выполнения действий.

• Перед выполнением операций со скобками нужно сначала решить задачи внутри скобок.
• Затем выполняются действия с умножением и делением.
• И, наконец, сложение и вычитание.

Пример:

ВыражениеРешение

5 — 2 * (6 + 1)

5 — 2 * 7 = -9

В данном примере, сначала выполнились действия в скобках (6 + 1 = 7), затем умножение (2 * 7 = 14), и, наконец, вычитание (5 — 14 = -9).

Таким образом, для успешного изучения выражений с целыми числами нужно знать основные арифметические действия, правила порядка выполнения действий и уметь применять их в практических задачах.

Примеры решения задач

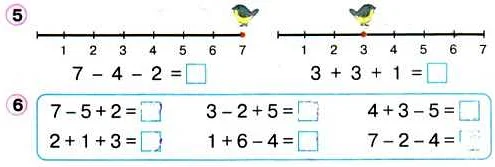
Вот несколько примеров решения задач для первоклассников:

1. Пример 1У Лены было 3 конфеты, она купила еще 2. Сколько у нее теперь конфет?Решение:

   Чтобы найти общее количество конфет, нужно сложить 3 и 2.

   3 + 2 = 5

   У Лены теперь 5 конфет.

2. Пример 2На столе лежало 7 яблок. Сколько яблок останется, если два из них съесть?Решение:

   Чтобы найти количество яблок, которое останется, нужно из 7 вычесть 2.

   7 — 2 = 5

   Останется 5 яблок.

3. Пример 3Коля набрал 8 камней, а Вася — 4. Сколько всего камней у них?Решение:

   Чтобы найти общее количество камней, нужно сложить 8 и 4.

   8 + 4 = 12

   У Коли и Васи вместе 12 камней.

Такие задачи помогают ребенку лучше понять и запомнить математические операции и начать применять их на практике.

Задачи на выражения для 1 класса

1. Сложение чисел в выражении:

У Пети было 3 красных шарика. Мама купила ему еще 2 зеленых шарика. Сколько всего шариков у Пети?

• 3 + 2 = 5

2. Вычитание чисел в выражении:

У Маши было 7 кубиков, но она отдала 3 кубика Саше. Сколько кубиков осталось у Маши?

• 7 — 3 = 4

3. Сложение и вычитание чисел:

У старшей сестры было 5 конфет, а у младшей — 3. Старшая сестра дала младшей 2 конфеты. Сколько конфет осталось у старшей сестры?

• 5 — 2 = 3

Сколько конфет у младшей сестры?

• 3 + 2 = 5

4. Умножение числа на число:

Мама купила Пете 4 коробки печенья. В каждой коробке было по 10 печеньек. Сколько печенек купила мама?

• 4 * 10 = 40

5. Деление числа на число:

У Пети было 16 конфет. Он решил разделить их поровну между своими 4 друзьями. Сколько конфет досталось каждому другу?

• 16 / 4 = 4

Сбор и разбор выражений

Сбор и разбор выражений — это процесс составления и разложения математических выражений. В первом классе детям представляются элементарные математические операции: сложение, вычитание, умножение, деление. Далее они изучают порядок действий, который необходимо соблюдать при выполнении вычислений.

Для того чтобы научиться собирать выражения, детям необходимо понимать каждый элемент. Они узнают, что цифры — это числа, а знаки +, -, *, / обозначают операции. Для того, чтобы собрать выражение, нужно правильно расставить скобки и операции в соответствии с правилами порядка действий.

Разбор выражений — это обратный процесс, когда мы раскладываем выражение на составляющие элементы. Если мы берем выражение 2 + 3 =, то можем разложить его на два слагаемых — 2 и 3 и знак операции — +.

Детям можно предложить задания на сбор и разбор выражений, чтобы они могли закрепить полученные знания. Например, можно привести выражение 4 + 2 — 1 = и попросить ребенка разложить его на 4, 2, 1 и знаки +, -. Также можно предложить задачки на сбор выражений, например, составить выражение из чисел 2, 4, 6 и знаков + и -.

Изучение сбора и разбора выражений помогает детям развивать логическое мышление и умение мыслить абстрактно. Кроме того, это основа для дальнейшего изучения более сложных математических операций.

Простые задачи на составление выражений

Для начала, что такое выражение в математике? Это математическая запись, состоящая из чисел, знаков операций и переменных. Выражение может быть вычислено, если значения переменных и порядок операций известны.

Рассмотрим простые задачи на составление выражений:

• Сумма чисел 2 и 3: 2 + 3
• Разность чисел 5 и 3: 5 — 3
• Произведение чисел 4 и 3: 4 * 3
• Частное чисел 10 и 2: 10 / 2

Также можно решать более сложные задачи на составление выражений, используя скобки для определения порядка выполнения операций. Например:

Задача:	Сколько будет 10, если из 20 вычесть 5 и умножить результат на 3?
Выражение:	(20 — 5) * 3
Ответ:	45

Таким образом, для решения задач на составление выражений необходимо понимать значения операций и правильно определять порядок их выполнения. Это поможет успешно решать более сложные математические задачи в будущем.

Задачи на решение выражений с использованием приоритетов операций

Для решения выражений с использованием приоритетов операций нужно знать, какие операции выполнять первыми, а какие последними. Самый высокий приоритет имеют скобки, затем умножение и деление, а потом сложение и вычитание.

Например, в выражении 3 + 4 * 2 сначала нужно выполнить умножение, потом сложение. Таким образом, правильный ответ – 11.

Решите следующие задачи на решение выражений:

• Вычислите значение выражения (5 + 3) * 2. Ответ: 16.
• Вычислите значение выражения 4 * 2 + 3 * 2. Ответ: 14.
• Вычислите значение выражения 12 / 4 + 2 * 3. Ответ: 9.

Будьте внимательны при выполнении задач и не забывайте следовать приоритетам операций!

Игры и упражнения для изучения выражений

Изучение математических выражений может быть интересным и увлекательным, особенно для первоклассников. Использование игр и различных упражнений поможет детям лучше понимать материал и запоминать его на долгое время.

Одно из популярных упражнений — это составление выражений из деталей. Например, можно использовать магнитные цифры, чтобы дети могли соединять их и составлять простые математические выражения. Также для этой цели можно использовать карточки с изображениями объектов, которые дети будут складывать или вычитать.

Для развития логического мышления можно использовать игры, в которых дети должны решать задачи по логике и составлять простые выражения. Например, можно использовать игру «Кто есть кто», где дети задают вопросы, чтобы отгадать, кто находится на карточке.

Для закрепления материала можно использовать различные варианты заданий. Например, дать детям задание посчитать определенное количество предметов на картинке и записать это в виде математического выражения. Либо можно дать задание составить выражение на время, чтобы дети могли тренировать свои навыки быстрого и точного вычисления.

Важно помнить, что игры и упражнения должны быть интересными и доступными для детей. Они должны стимулировать детей к дальнейшему изучению математических выражений и создавать положительную атмосферу для обучения. Поэтому, выбирайте упражнения с учетом возраста и уровня подготовки учащихся, чтобы они могли успешно справляться с заданиями и получать удовольствие от процесса обучения.

Игры на составление выражений

В играх на составление выражений дети могут учиться собирать простые математические формулы и различать операции, такие как сложение, вычитание, умножение и деление. Эти игры также могут помочь детям осознать, что математические формулы могут быть записаны в виде символов и знаков, и что эти символы и знаки представляют различные математические операции.

Одной из популярных игр на составление выражений является игра «Бинго». Дети выбирают карточки с числами, затем выбирают два числа и объединяют их с помощью математической операции. Затем они ищут результат в карточке и отмечают его. Когда они отметят все числа на карточке, они говорят «Бинго» и выигрывают игру.

Другая игра на составление выражений — «Математические головоломки». Дети должны выбрать головоломку и собрать выражение из набора чисел и математических знаков, чтобы получить правильный ответ. Эта игра помогает детям развивать логическое мышление и учиться работать с числами и знаками.

• Для изучения математики и выражений не обязательно делать это скучно и трудно — игры могут сделать процесс увлекательным и необычным.
• Игры на составление выражений — прекрасный метод практиковаться и развиваться в этой важной области знаний.

Упражнения на раскрытие скобок

Раскройте скобки и выполните операции:

1. 5 + (2 + 3) = 10
2. 7 — (4 — 1) = 4
3. 6 — (2 + 1) = 3
4. 8 + (3 — 2) = 9

Раскройте скобки и упростите выражения:

• 2 x (4 + 1) = 10
• 3 x (2 + 3) = 15
• 4 x (7 — 2) = 20
• 5 x (3 — 1) = 10

Раскройте скобки и решите уравнения:

УравнениеОтвет

9 — (4 + x) = 2	x = 3
6 + (2 — x) = 11	x = -5
8 — (x — 2) = 3	x = 7
5 x (3 + x) = 40	x = 2

Решение примеров с использованием приоритетов операций

При решении математических примеров необходимо учитывать приоритет операций. Сначала выполняются операции в скобках, затем умножение и деление, а после сложение и вычитание. Например, если пример включает скобки, то сначала решаются действия внутри скобок.

Однако, если скобок нет, но есть умножение и деление, то их необходимо выполнить перед сложением и вычитанием. Например, если пример выглядит так: 5 + 4 × 2, то нужно сначала умножить 4 на 2, а потом прибавить 5. Таким образом, 5 + 8 = 13.

Когда в примере нет скобок, умножения и деления, а только сложение и вычитание, то действия выполняются последовательно слева направо. Например, если пример выглядит так: 10 — 2 + 5 — 1, то нужно сначала вычесть 2 из 10, затем прибавить 5 и вычесть 1. Таким образом, 10 — 2 + 5 — 1 = 12.

Правильное выполнение примеров с использованием приоритетов операций необходимо для получения верных результатов и запоминания математических правил.

Преимущества изучения выражений в математике для 1 класса

Усвоение базовых понятий математики

Изучение выражений в математике для 1 класса позволяет детям усвоить базовые понятия математики, такие как числа, знаки операций, их приоритетность и т.д. Эти знания будут полезны на протяжении всей учёбы, в том числе в решении более сложных задач.

Развитие логического мышления

Изучение выражений в математике, а также решение задач на их основе, помогает развивать логическое мышление ребёнка. В ходе выполнения заданий ребёнок учится абстрагироваться от лишних деталей и находить связь между элементами задания, что важно для умения решать проблемы в будущем.

Подготовка к изучению более сложных задач

Изучение выражений в математике для 1 класса является первым шагом на пути к решению более сложных задач. Понимание базовых понятий математики и навыки логического мышления, полученные в ходе этого изучения, помогут ребёнку легче усваивать новые материалы и решать более сложные задачи в будущем.

Повседневное применение математики

Знания, полученные в ходе изучения выражений в математике для 1 класса, находят применение в повседневной жизни. Например, при покупке товаров в магазине, при рассчете времени на выполнение заданий и т.д. Умение быстро и правильно производить вычисления является навыком, необходимым в различных сферах жизни.

Улучшение навыков математики

Математика – это не только один из основных предметов в школе, но и незаменимый инструмент в жизни каждого человека. Улучшение навыков математики поможет нам не только в решении повседневных задач, но и в дальнейшем обучении и карьере.

Как развивать свои математические навыки? Во-первых, необходимо понимать основные математические операции, такие как сложение, вычитание, умножение и деление. Эти операции нужно учить наизусть и затем тренировать их выполнение на примерах. Постепенно, подобно строительству фундамента, вы начнете понимать, какие операции следует применять в различных ситуациях.

Во-вторых, необходимо активно использовать математику в своей жизни. Вы можете заняться подсчетом своих расходов, посчитать необходимую сумму налогов, рассчитать время, необходимое для выполнения задачи. Чем больше практического опыта вы получите в решении математических задач, тем быстрее и эффективнее вы будете выполнять их в будущем.

• Не бойтесь ошибаться. Ошибки – это нормальное явление в процессе обучения, особенно в математике. Каждая ошибка – это возможность для улучшения своих навыков. Решив задачу неверно, анализируйте свои ошибки и рассматривайте их как опыт.
• Учите математику в игровой форме. Для того чтобы математика была интересной, используйте игрушки, пазлы, конструкторы, головоломки. Во время игры вы будете не только получать знания, но и развивать логическое мышление.
• Не забывайте о грамотном режиме дня. Хороший сон и правильное питание помогут сохранить высокую концентрацию и восприимчивость. Время занятий математикой лучше выбирать в те часы, когда вы чувствуете наибольшую работоспособность.

Важно помнить, что улучшение навыков математики требует времени и усилий. Только регулярная практика, постоянное обновление знаний и умения применять их в жизни помогут достичь успеха в этом предмете.

Развитие логического мышления

Логическое мышление – это способность человека к анализу и решению проблем с помощью логических операций. Оно очень важно для решения математических задач и не только.

В школьной программе развитие логического мышления начинается с первого класса. Ученики изучают азы логики через игры, загадки, головоломки и другие развивающие упражнения.

Важно помнить, что регулярные упражнения и тренировки развивают логическое мышление, как мышцы. Чем больше ребенок тренирует свой мозг, тем лучше он умеет решать задачи.

Существует множество методик, которые помогают развивать логическое мышление у детей. Например, игры на логику, мозговые штурмы, задачи на логическое мышление и т.д. Важно подбирать задания, подходящие возрасту и уровню развития ребенка.

Также не стоит забывать, что развитие логического мышления связано с обучением математике. Чем больше ребенок учится решать математические задачи, тем больше тренируется и развивает свой мозг.

Важно, чтобы школа и родители совместно работали над развитием логического мышления у детей. Регулярные упражнения, различные игры и задания помогут не только легче учится в школе, но и хорошо подготовят ребенка к жизненным ситуациям, где потребуется логическое мышление.

Подготовка к изучению алгебры в старших классах

Изучение алгебры начинается сравнительно рано, но глубокое знание ее основных концепций требует серьезной работы и усилий. Подготовка к изучению алгебры должна начинаться еще в начальной школе, чтобы ученики имели достаточный уровень знаний и навыков, чтобы успешно продвигаться дальше.

Одним из главных элементов подготовки к изучению алгебры является понимание базовых математических понятий, таких как измерение, фундаментальные операции и пропорции. Эти понятия должны быть полностью понятны и могут быть позволительно применены к решению математических задач.

Другой важный аспект подготовки к изучению алгебры — развитие мышления и умение решать математические проблемы. Ученики должны быть учены не только решать типовые задания, но и находить свои собственные способы решения. Подобное отношение обеспечивает необходимые инструменты учащимся для эффективной работы в алгебре и дальнейшего успеха в математике и науке.

Наконец, может быть полезным знать основы логики и грамматических баз данных, которые будут использоваться в алгебре. Это может включать в себя понимание терминов как «и», «или», и «не» и умение работать с простыми уравнениями и формулами.

Без соответствующей подготовки к изучению алгебры, ученики могут иметь проблемы с пониманием концепций и проблемами решения задач, что может привести к неудачам на уровне школы и дальнейшим трудностям в теме. Однако, при должной подготовке и увлеченности, ученики могут наслаждаться изучением алгебры и достигнуть успехов в дальнейшей жизни.

Вопрос-ответ:

Что такое выражение в математике?

Выражение в математике — это сочетание чисел, знаков операций и переменных. Например, 2 + 3 или 5x — 2. Оно позволяет вычислять результат математической операции.

Как изучать выражение в математике в 1 классе?

Изучение выражений в математике начинается с простых заданий на сложение и вычитание чисел. Затем дети учатся работать с переменными, использовать скобки и выполнять действия с множителями. Для более эффективного изучения этой темы можно использовать игры, задачи и визуальные материалы.

Как правильно складывать и вычитать выражения?

Чтобы сложить или вычесть выражения, нужно сначала раскрыть скобки, затем перемножить множители и добавить или вычесть полученные результаты. Важно не забывать следить за знаками операций, чтобы не допустить ошибок в решении.

Какие виды переменных бывают в выражениях?

В выражениях можно использовать разные виды переменных, например, буквы или знаки, которые обозначают какие-то значения или величины. В математике обычно используются буквы x, y, z и т.д.

Что такое операции в математике?

Операции в математике — это математические действия, выполняемые над числами или переменными. Они могут быть различными: сложение, вычитание, умножение и т.д. При выполнении операций важно следить за порядком их выполнения и при необходимости использовать скобки.

Как правильно применять скобки в выражениях?

Скобки используются для группирования частей выражения и определения порядка выполнения операций. Сначала выполняются операции внутри скобок, затем — остальные, в порядке установленном по правилам математики. Если в выражении несколько пар скобок, сначала выполняются операции внутри наиболее внутренних скобок.

Как изучение выражений влияет на развитие математических навыков у первоклассников?

Изучение выражений в математике способствует развитию логического мышления, абстрактного и критического мышления. Это помогает детям научиться решать различные задачи, осознавая порядок операций и выбирая правильные действия. Также, изучение выражений помогает подготовиться к более сложным математическим задачам в будущем.