Как решать задачи по высшей математике: простые и эффективные методы

Узнайте, как решать задачи по высшей математике: алгебре, геометрии и математическому анализу. Полезные советы и стратегии для успешного освоения сложных математических концепций.

Высшая математика является одним из ключевых элементов современного мира, она находит свое применение в самых разных областях жизни: от физики до экономики и финансов. Решение задач и уравнений из высшей математики лежит в основе многих научных открытий и технологических достижений.

Однако, несмотря на все прекрасные качества высшей математики, она является достаточно сложной дисциплиной, требующей большого знания и понимания. Решение уравнений и задач требует не только знания определенных формул и методов, но и умения грамотно и логически мыслить.

В данной статье мы рассмотрим основные методы и подходы к решению задач и уравнений из высшей математики. Мы попытаемся разобраться в ключевых понятиях и формулах, которые используются в этой дисциплине, и научимся решать задачи и уравнения с помощью этих знаний. Надеемся, что после прочтения этой статьи, вы сможете легко решать задачи и уравнения из высшей математики и применять свои знания на практике.

Основы высшей математики

Высшая математика – это раздел математики, который занимается изучением абстрактных объектов и их свойств. Она включает в себя такие разделы, как алгебра, геометрия, математический анализ, теорию вероятностей, дифференциальные уравнения и другие.

Основы высшей математики начинаются с изучения математических объектов, таких как числа, функции, графики и матрицы. В дальнейшем, они изучаются более подробно и углубленно, что позволяет решать сложные задачи и применять математические методы в различных областях науки и техники.

Одной из основ высшей математики является алгебра. Она изучает алгоритмы и методы работы с числами, переменными и алгебраическими выражениями. Она помогает решать уравнения, системы уравнений и другие задачи, связанные с алгебраическими операциями.

Другой важный раздел высшей математики – это математический анализ. Он изучает пределы, производные, интегралы и ряды. Математический анализ используется, например, для моделирования физических процессов, определения максимумов и минимумов функций и решения дифференциальных уравнений.

В целом, основы высшей математики – это основы для понимания и решения сложных математических задач. Различные разделы этой науки взаимосвязаны и используются вместе, чтобы решать реальные проблемы и создавать новые технологии.

Как решать задачи на производную

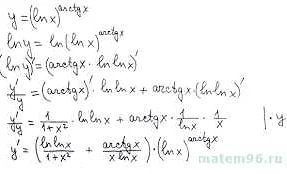
Производная является одной из важнейших тем в высшей математике, поэтому знание способов ее решения необходимо для успешного изучения математики. В этой статье мы рассмотрим основные методы решения задач на производную.

Шаг 1: Определить функцию, для которой нужно вычислить производную и найти ее одиночную или частную производную. Для этого используйте правила дифференцирования, которые уже изучили, либо примените формулы.

Шаг 2: Решите уравнение, равное нулю, чтобы найти стационарные точки функции. Это могут быть экстремумы, точки перегиба или производные второго порядка.

Шаг 3: Постройте график функции и выделите области, где функция возрастает или убывает. Оцените, есть ли точки экстремума, и найти их координаты.

Шаг 4: Проверьте, удовлетворяют ли найденные точки экстремума условиям. Для этого можно использовать правило знаков производной или вычислить производную второго порядка.

Шаг 5: Запишите ответ на вопрос задачи. Обычно это может быть максимум, минимум или точка перегиба. Обязательно проверьте свой ответ и убедитесь, что он логически корректен и соответствует условию задачи.

В заключение, решение задач на производную — это техника, которая может использоваться в различных областях математики, причем она может быть очень полезна в повседневной жизни. Если вы изучите эту тему и научитесь ее применять, то вы сможете решать многие сложные задачи и повысите свой уровень знаний в математике.

Как решать задачи на интеграл

Решение задач на интеграл требует от студента знания основных интегральных формул и умения применять их для нахождения интегралов. Важно понимание геометрического значения интеграла.

Для решения задач на интеграл необходимо:

• Привести подынтегральное выражение к виду, содержащему степени многочлена, тригонометрические, логарифмические функции и т.д.
• Использовать интегральные формулы для нахождения значения интеграла.
• Найти константу интегрирования, при необходимости.
• Проверить полученный результат на правильность.

При решении задач на интеграл необходимо учитывать особенности каждого конкретного случая. Например, интегрирование функций, содержащих корневые выражения, может требовать применения замены переменной.

Важно помнить, что интегрирование — это обратный процесс дифференцирования. Поэтому при применении интегральных формул необходимо проверять корректность дифференцирования полученного результата.

Для решения задач на интеграл также могут применяться методы интегрирования по частям и замена переменной. Кроме того, для интегрирования сложных функций могут применяться численные методы.

Как решать уравнения с одной неизвестной

При решении уравнений с одной неизвестной нужно найти значение этой неизвестной, которое удовлетворяет равенству выражения, содержащего эту неизвестную. Такие уравнения могут быть выражены в виде линейных уравнений, квадратных уравнений, уравнений с рациональными или иррациональными выражениями и т.д.

Первым шагом при решении уравнений с одной неизвестной является приведение всех членов к одному и тому же виду. Это может включать в себя вынос общих множителей, раскрытие скобок и т.д. Затем нужно использовать правила алгебры для изолирования неизвестной на одной стороне равенства.

Важно помнить, что при каждом изменении равенства нужно выполнять аналогичное изменение на обеих сторонах равенства, чтобы сохранить его верность. Также нужно учитывать возможные условия на заданную неизвестную, например, ограничения на область определения функций.

При решении уравнений с одной неизвестной могут быть полезными методы, такие как графический метод, метод подстановки, метод коэффициентов и так далее. Важно выбирать метод, который наиболее подходит для конкретной задачи.

Изучение и практика решения уравнений с одной неизвестной помогут улучшить математические навыки и способности, что может быть полезно как в повседневной жизни, так и в профессиональной деятельности.

Как решать уравнения с несколькими неизвестными

Решение уравнений с несколькими неизвестными требует использования системы уравнений. Для начала необходимо записать уравнения в виде системы.

Система уравнений — это набор уравнений, которые решаются одновременно. Каждое уравнение содержит несколько неизвестных, которые необходимо найти.

Для решения системы уравнений применяются различные методы, включая метод подстановки, метод коэффициентов и метод определителей. Выбор метода зависит от конкретной системы уравнений.

В методе подстановки неизвестные выражаются через другие неизвестные, что позволяет сократить количество неизвестных в системе. Метод коэффициентов основан на выражении неизвестных через коэффициенты уравнений, в таком случае система приводится к матричному виду. Метод определителей также использует матричные выкладки, но для нахождения неизвестных применяется вычисление определителей.

Для более сложных систем уравнений может потребоваться использование комбинации методов или численных методов. В любом случае для решения системы уравнений необходимо тщательно анализировать ее состав и применять наиболее подходящий метод.

Пример:

Решить систему уравнений:

• x + y + z = 6
• 2x — y + z = 3
• x + 3y — 2z = 7

Для начала выберем метод, подходящий для данной системы. Поскольку все коэффициенты числовые, применим метод коэффициентов.

Приведем систему к матричному виду:

1	1	1	6
2	-1	1	3
1	3	-2	7

Следующий шаг — вычисление определителя матрицы:

| 1 1 1 |

| 2 -1 1 | = (-1) * | 1 3 1 |

| 1 3 -2 |

det = -1 * (-2 — 3 — 3 — 2 + 2 — 1) = -1

Теперь найдем определители матриц, полученных вычеркиванием столбцов, соответствующих каждой неизвестной:

| 6 1 1 |

| 3 -1 1 | = (-1) * | 7 1 1 |

| 7 3 -2 |

det_x = -1 * (3 + 2 — 1 — 7 — 3 + 42) = -32

det_y = -1 * (-6 — 2 — 1 — 21 + 12 — 14) = 50

det_z = -1 * (6 — 1 — 14 — 18 — 1 + 9) = -11

Таким образом, x = 32/-1 = -32, y = 50/-1 = -50 и z = -11/-1 = 11.

Ответ: x = -32, y = -50, z = 11.

Как решать системы уравнений

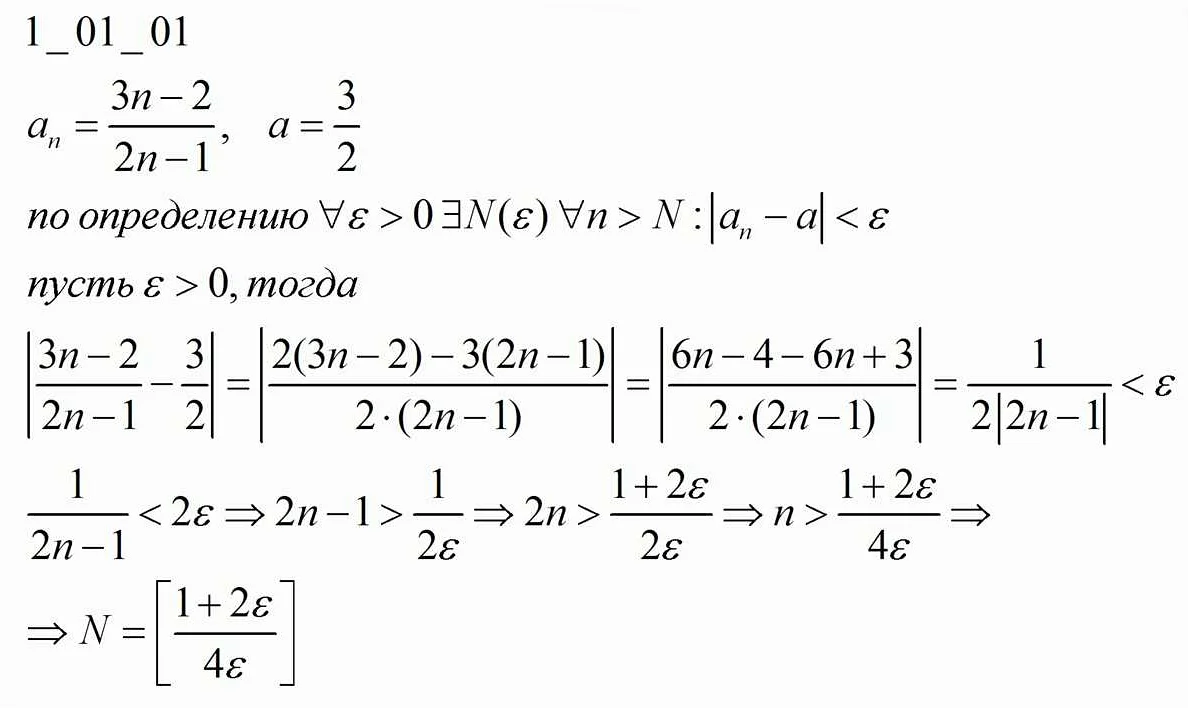
Система уравнений это набор уравнений, связанных друг с другом, которые нужно решить одновременно, чтобы найти значения неизвестных переменных. Системы уравнений являются одной из основных тем в высшей математике, так как они используются во многих областях, включая физику, экономику и инженерию.

Существует несколько методов, которые можно использовать для решения систем уравнений. Один из самых распространенных методов — метод Крамера, который использует определитель матрицы коэффициентов системы. Другой популярный метод — метод Гаусса, который использует элементарные преобразования строк матрицы, чтобы привести ее к треугольному виду.

При решении систем уравнений важно следить за правильностью выполнения каждого шага, чтобы получить правильный ответ. Для этого можно использовать упрощенные методы, например, метод графического представления, при котором уравнения системы изображаются на графике и пересечение их линий показывает решение системы.

Важно помнить, что решение систем уравнений может быть единственным, не иметь решения или иметь множество решений, в зависимости от соотношения коэффициентов в уравнениях. Поэтому при решении необходимо учитывать все возможные варианты и проверять полученное решение на правильность, подставляя значения в исходные уравнения.

Как решать уравнения и системы уравнений с параметрами

Уравнения и системы уравнений с параметрами это особая группа математических выражений, состоящих из неизвестных переменных и параметров. Чтобы решить такие уравнения, нужно сначала найти значения параметров. Для этого можно поставить определенные условия на значения параметров или воспользоваться промежуточными значениями их компонентов.

После нахождения параметров, необходимо решить уравнения с использованием стандартных методов алгебры. Если в уравнениях встречаются параметры, то искомые значения переменных будут зависеть от значений параметров. В таком случае решения уравнений следует записать в виде зависимости переменных от параметров.

Решение системы уравнений с параметрами также осуществляется путем нахождения значений параметров и дальнейшего решения уравнений. Если в системе имеется несколько уравнений, то необходимо последовательно решать каждое из них, вводя изменения в значения параметров и используя предыдущие результаты, пока все уравнения не будут решены.

При решении уравнений и систем уравнений с параметрами необходимо учитывать возможные ограничения на значения параметров и переменных. Если в уравнениях присутствуют наибольшие или наименьшие значения переменных, то следует проверить, что найденные значения соответствуют определенным допустимым интервалам или условиям.

В заключении, решение уравнений и систем уравнений с параметрами требует тщательного анализа и понимания принципов алгебры. Основной задачей является нахождение всех значений параметров и их влияния на переменные. Когда это будет сделано, уравнения можно решить стандартными методами.

Как решать задачи на минимум и максимум функции

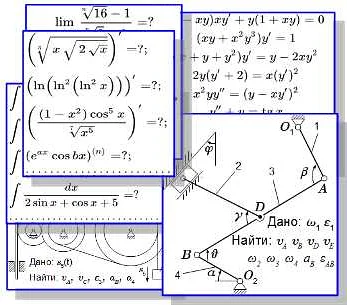
Решение задач на минимум и максимум знакомо нам еще из школьной программы математики. Для решения таких задач необходимо уметь находить экстремумы функции.

Что такое экстремум функции? Экстремум функции – это точка, в которой функция достигает максимального или минимального значения на заданном интервале.

Как найти экстремум функции? Решение такой задачи начинается с нахождения производной функции. Далее нужно найти все точки, в которых производная равна нулю или не существует.

Что делать дальше? После нахождения всех критических точек необходимо проверить, являются ли они точками минимума или максимума. Для этого используется вторая производная функции. Если в критической точке вторая производная положительна, то это точка минимума, а если она отрицательна – то максимума. Если же вторая производная равна нулю, то следует использовать дополнительные методы анализа.

Пример решения задачи на минимум функции:

1. 1. Найдем производную функции f(x) = x^3 — 3x^2 — 9x + 5

f’(x) = 3x^2 — 6x — 9

1. 1. Найдем критические точки f’(x) = 0

3x^2 — 6x — 9 = 0

x1 = -1, x2 = 3

1. 1. Найдем значения второй производной в критических точках

f’’(x1) = 6 > 0 – точка минимума

f’’(x2) = 18 > 0 – точка минимума

1. 1. Найдем значения функции в найденных точках

f(-1) = 8, f(3) = -19

1. Ответ: минимальное значение функции равно -19 и достигается в точке x = 3

Таким образом, решение задач на минимум и максимум функций сводится к поиску критических точек функции и исследованию второй производной в этих точках.

Как решать задачи на нахождение площади фигур

Для того чтобы решать задачи на нахождение площади фигур, необходимо знать формулы для вычисления площади различных фигур. Например, для квадрата площадь вычисляется по формуле S = a^2, где a — длина стороны квадрата. Для прямоугольника площадь равна произведению длины на ширину: S = a * b.

Для треугольника площадь можно вычислить по формуле Герона: S = √(p * (p — a) * (p — b) * (p — c)), где p = (a + b + c) / 2, а a, b, c — длины сторон треугольника.

Для нахождения площади круга нужно использовать формулу S = πr^2, где r — радиус круга, а π (пи) — математическая константа, примерно равная 3,14.

Кроме того, для некоторых фигур можно использовать готовые формулы, например, для трапеции: S = ((a + b) / 2) * h, где a, b — основания трапеции, а h — высота, опущенная на основание.

При решении задач на нахождение площади фигур следует также обратить внимание на единицы измерения. Обычно площадь измеряется в квадратных сантиметрах, квадратных метрах или квадратных километрах, но могут быть и другие единицы измерения, например, квадратные дюймы в англоязычных странах.

Если задача не предполагает нахождения точной величины площади, а только сравнение или оценку, то можно использовать приближенные методы, например, приближенно разбивать фигуру на геометрические фигуры, для которых известны формулы площадей.

Как решать задачи на нахождение объема тел

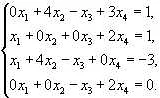
Чтобы решать задачи на нахождение объема разных тел, важно знать и понимать их форму и основные характеристики. Необходимо также знать формулы расчета объема каждого из тел. Ниже приведены некоторые из наиболее часто встречающихся тел и формулы для их объема:

• Параллелепипед: V = a * b * c
• Куб: V = a * a * a
• Цилиндр: V = π * r * r * h
• Шар: V = (4/3) * π * r * r * r
• Конус: V = (1/3) * π * r * r * h

Кроме того, для решения задач необходимо уметь читать условия задач и правильно применять формулы. Иногда они требуют применения различных свойств и формул из разных областей математики. Поэтому, важно систематически изучать математику, чтобы иметь необходимые знания и умения.

Когда решаете задачи на расчет объемов тел, помните, что единицы измерения также могут оказывать влияние на решение задачи. Например, если в условии задачи указаны размеры в сантиметрах, а вы используете метры в формуле для объема, ответ будет неверным. Поэтому, важно всегда внимательно читать условия и применять правильные единицы измерения.

Вопрос-ответ:

Какие методы решения дифференциальных уравнений существуют?

Существует множество методов решения дифференциальных уравнений, включая метод разделения переменных, метод неопределенных коэффициентов, метод вариации произвольной постоянной, метод Лапласа и многие другие. Каждый из них подходит для решения определенного класса дифференциальных уравнений.

Как определить, какой метод решения уравнений лучше использовать?

Выбор метода зависит от типа уравнения и его условий. Важно проанализировать тип уравнения, его порядок, граничные условия и другие факторы. Часто бывает полезно попробовать несколько различных методов и сравнить результаты.

Какие методы могут использоваться для решения сложных многомерных уравнений?

Для решения сложных многомерных уравнений могут использоваться методы численного анализа, такие как метод конечных элементов, метод конечных разностей, метод монте-карло и другие. Эти методы позволяют получить приближенное решение уравнения в целом или в определенных точках.

Как можно сократить время решения уравнений?

Один из способов сократить время решения уравнений — использовать специализированные программные пакеты, такие как MATLAB, Mathematica или Maple. Эти программы позволяют автоматизировать большую часть работы и потому упрощают процесс. Кроме этого, разложение уравнений на более простые компоненты может существенно сократить время решения.

Как организовать свою работу в процессе решения математических задач?

При работе с математическими задачами следует начинать с анализа проблемы и выявления необходимых данных. Закрепление понимания задачи, формулировка гипотезы и создание плана действий помогут снизить время и усилить конечный результат. Далее следует решать задачу шаг за шагом, проверяя результаты на каждом этапе.

Как оценить правильность решения математической задачи?

Оценка правильности решения математической задачи может осуществляться по различным критериям, например, сравнением полученного результата со стандартным решением или проверкой на соответствие условиям задачи. Кроме этого, стоит убедиться, что использованные формулы и методы решения соответствуют данной проблеме.

Как можно применить высшую математику в повседневной жизни?

Высшая математика может быть использована в различных областях, включая науку, финансы, технологии, медицину и многие другие. Например, алгоритмы машинного обучения применяются для распознавания образов и проверки безопасности. Криптография — является областью математических методов для защиты данных. Оптимизация процессов является областью, где используются различные методы определения оптимальных параметров. Это удобно в области производства, разработки продукта и других областях.

Видео по теме: