Почему для платона главная наука математика

Платон считал математику главной наукой, поскольку она обладает строгими логическими законами и истинами, которые являются основой для всех других наук и философии. В статье рассмотрены основные аргументы, представленные Платоном в пользу этой идеи, а также обсуждаются примеры из его диалогов, подтверждающие его убеждения.

Математика — это удивительная наука, которая имеет глубокие корни и огромное значение для развития человечества. Одним из величайших философов, которые понимали и ценили важность математики, был Платон. Его интерес к этой науке был настолько глубоким, что он считал ее главной основой для понимания мира и общества.

Для Платона математика была не только способом описания и изучения физического мира, но и инструментом для познания истины. Он верил, что математические объекты и законы являются вечными и независимыми от человеческого опыта. Они существуют в своей собственной реальности и могут быть познаны разумом.

В своих диалогах Платон многократно обращается к математике и использует ее в качестве аналогии для объяснения своих философских идей. Он видел в математике идеальные формы и истину, которые могут быть достигнуты только через разумное мышление и абстрактное рассуждение.

«Математика — это наука о том, что не может быть иначе»

Для Платона математика была неотъемлемой частью его учения о идеальных формах и разделения мира на две реальности: мир чувственного и мир идеального. Математика позволяла ему понять и описать законы и структуру идеального мира, который был идеальным идеального, а идеального — идеального. Математика для Платона была ключом к пониманию космоса и его организации.

Таким образом, Платон использовал математику не только для описания физического мира, но и для развития истинного знания о мире и человечестве. Он утверждал, что математические идеи и законы являются неотъемлемым компонентом нашего мышления и позволяют нам познать мир в его идеальной форме.

Значение математики для Платона: основы и главная наука

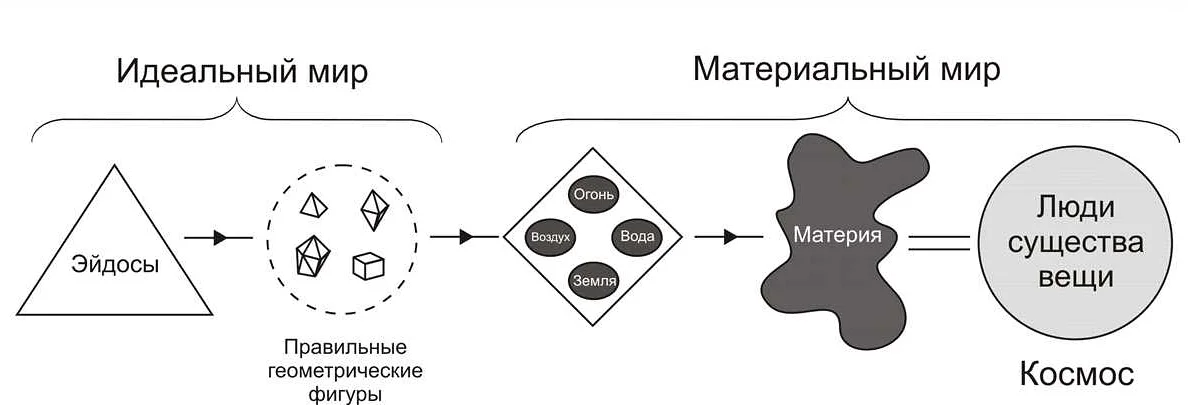
Математика играла важную роль в философии Платона и считалась одной из основных наук. Для Платона математика была не только инструментом для изучения физического мира, но и способом познания истины и духовного развития.

Платон считал, что математические объекты, такие как числа и геометрические фигуры, существуют независимо от мира чувственного опыта. Они являются идеальными и вечными сущностями, которые можно познать только разумом. Математика для Платона была языком, на котором говорят идеи, и путь к пониманию высших истин.

Платон считал, что математика помогает развивать логическое мышление, абстрактное мышление и способность к анализу и рассуждению. Он считал, что изучение математики не только развивает ум, но и помогает раскрыть потенциал человека в других областях знания.

Для Платона математика была основой для других наук. Он считал, что знание о математических идеях и законах мира является фундаментом для изучения физики, музыки, астрономии и других наук. Математические принципы и законы, по мнению Платона, лежат в основе устройства мира и позволяют понять его гармонию и порядок.

Таким образом, для Платона математика была не только наукой о числах и фигурах, но и универсальным средством познания истины и развития мышления. Она была основой для изучения других наук и помогала понять устройство мира и его гармонию.

Видео по теме:

Влияние математики на философию Платона

Математика играла важную роль в философии Платона и оказала значительное влияние на его учение. Для Платона математика была не просто наукой, а основой для построения его философской системы.

Математика предоставляла Платону инструмент для изучения и понимания мира и его законов. Он рассматривал математические объекты, такие как числа и геометрические фигуры, как идеальные и незыблемые формы, существующие независимо от конкретных объектов в мире чувственно воспринимаемых вещей.

Философия Платона основывалась на идеях и идеалах, которые он считал вечными и безизменными. Он считал, что математические идеи представляют собой наиболее чистую форму познания мира и являются основой для понимания реальности.

Математика также влияла на методологию философии Платона. Он использовал математические методы, такие как дедукция и абстракция, для развития своих философских идей. Он стремился к достижению идеальной истины и использовал математическую логику для достижения этой цели.

Таким образом, математика была не просто одной из наук, изучаемых Платоном, но представляла собой основу его философской системы. Она позволяла ему понять природу реальности и достичь истины. Влияние математики на философию Платона проложило путь к развитию математической философии и имело долгосрочное влияние на философию и науку в целом.

Роль математики в формировании понятий и идей Платона

Платон считал, что математика является наиболее достоверным источником знания, так как ее объектами являются идеи, которые существуют вне нашего мира чувственного восприятия. Он верил, что идеи являются основой реальности и отражают сущность всех вещей. Именно поэтому математика была для него главной наукой.

Платон рассматривал математику как средство для познания вечных идеальных форм. Он считал, что математические объекты, такие как числа, геометрические фигуры и пропорции, отражают идеи и существуют независимо от конкретных объектов в мире чувственного опыта.

Математика воспитывает абстрактное мышление и способность рассуждать логически, что важно для достижения высшей истины. Платон считал, что только тот, кто обладает математическими знаниями и умеет их применять, способен проникнуть в мир идей и познать настоящую реальность.

Идеи Платона о роли математики оказали влияние на развитие философии и науки. Его учение о математике как основе познания вечных истин стало одним из фундаментальных принципов западной философии и стимулировало развитие математики как науки.

Математика как ключевая составляющая диалектики Платона

Для Платона математика была не только наукой, изучающей формы и отношения вещей, но и мощным инструментом для развития мышления. Он считал, что математические идеи и принципы, такие как геометрия и арифметика, являются основой для понимания фундаментальных понятий и истинных идей.

Математика, по мнению Платона, позволяет увидеть всеобщую гармонию и порядок мира. Он считал, что математические объекты и законы существуют независимо от нашего опыта и сознания, и именно через изучение математики мы можем приблизиться к истине и познать реальность.

Кроме того, Платон рассматривал математику как средство для развития рационального мышления и критического анализа. Он утверждал, что изучение математики помогает развивать способность мыслить логически, анализировать и строить аргументацию. Таким образом, математика играет важную роль в формировании качеств мыслителя и философа.

Итак, математика является неотъемлемой частью диалектики Платона, используемой им как ключевой инструмент для достижения истины и познания мира. Она позволяет нам увидеть гармонию и порядок во вселенной, развивает наше мышление и способствует формированию критического анализа. Благодаря математике мы можем получить глубокое понимание фундаментальных истин и идей, которые лежат в основе нашего существования.

Отношение Платона к математической абстракции и реальности

Математика играла важную роль в философии Платона и считалась им одним из ключевых инструментов для познания истины. Он рассматривал математические объекты, такие как числа и геометрические фигуры, как образцы идеальных форм, которые существуют независимо от мира явления.

Платон считал, что наши чувственные восприятия и впечатления являются лишь отражением идеальных форм, которые существуют в мире идей. Математика, по его мнению, позволяет нам приблизиться к этим идеальным формам и понять их законы и отношения.

Для Платона математика была не просто набором абстрактных символов и формул, а способом познания истины и обращения к высшей реальности. Он считал, что математические идеи являются более реальными, чем та же самая материальная реальность, которую мы воспринимаем через наши чувства.

В своем диалоге «Федон» Платон приводит аналогию между математическими идеями и идеями о красоте и добродетели. Он утверждает, что так же, как мы можем понять и узнать о красоте или добродетели, несмотря на то, что мы никогда не видели их в чистом виде, так же мы можем понять и узнать о математических идеях через размышления и рассуждения.

Таким образом, для Платона математика была не только наукой, но и способом духовного роста и познания высших истин. Она позволяла ему приблизиться к идеальным формам и открыть для себя реальность, которая лежит за пределами чувственного мира.

Математические идеи Платона и их влияние на развитие науки

Одной из важных математических идей Платона является идея о существовании вечных и неизменных математических объектов, которые существуют независимо от нашего сознания. Это означает, что математические истины существуют вне нашего опыта и являются объективными и всеобщими.

Платон разделял математические объекты на два типа: видимые и невидимые. Видимые математические объекты — это конкретные математические фигуры и формы, которые можно наблюдать в мире. Невидимые математические объекты — это абстрактные идеи, которые существуют только в уме. Платон считал, что невидимые математические объекты более реальны и истинны, чем видимые.

Математические идеи Платона оказали значительное влияние на развитие науки. Концепция вечных и неизменных математических объектов стала основой для развития математики как науки. Она способствовала развитию логики и формализации математического мышления, что позволило сделать математику более точной и стройной.

Влияние идей Платона также заметно в других научных дисциплинах. Например, в физике, понятие о неизменности и объективности математических законов стало основой для развития фундаментальных законов природы. В химии, математические модели и формулы используются для описания и предсказания химических реакций и свойств веществ. В экономике, математические модели позволяют анализировать и предсказывать экономические процессы.

Таким образом, математические идеи Платона играют важную роль в развитии науки и позволяют нам понимать и объяснять мир вокруг нас. Они способствуют развитию логического мышления и формализации знаний, что делает науку более точной и надежной.

Значение математики в понимании метафизических аспектов мира

Математика играет важную роль в понимании метафизических аспектов мира, поскольку она предоставляет нам возможность абстрактного мышления и формализации неопределенных понятий. Метафизика, как философская дисциплина, занимается исследованием фундаментальных вопросов о природе реальности, бытии и сущности. В этом контексте, математика дает нам инструменты для анализа и структурирования абстрактных идей.

Платон считал математику главной наукой и высоко ценил ее вклад в понимание мира. Он считал, что математика является ключом к познанию истинной реальности. В своей идеальной теории форм, Платон утверждал, что математические объекты, такие как числа и геометрические фигуры, существуют независимо от физического мира и являются основой для понимания действительности.

Математика позволяет нам исследовать законы природы и создавать модели, которые помогают нам лучше понять мир вокруг нас. Она предоставляет нам язык для описания и изучения сложных феноменов и явлений. Математические модели могут помочь нам предсказать и объяснить различные аспекты мира, от движения планет до поведения частиц в физических системах.

Кроме того, математика играет важную роль в философии и эпистемологии, помогая нам разрабатывать и анализировать различные концепции и аргументы. Она предоставляет нам инструменты для логического рассуждения и формализации наших мыслей. Математический аппарат помогает нам развивать строгие доказательства и проверять логическую последовательность наших рассуждений.

Таким образом, математика играет важную роль в нашем понимании метафизических аспектов мира. Она предоставляет нам язык и инструменты для абстрактного мышления, анализа сложных явлений и формализации наших концепций. Благодаря математике мы можем лучше понять и объяснить фундаментальные вопросы о природе реальности и бытии.

Понятие идеальных форм и их связь с математическими концепциями

Связь между понятием идеальных форм и математическими концепциями заключается в том, что математика является одним из способов познания идеальных форм. Платон считал математику самой высокой и самой важной наукой, поскольку она позволяет нам понять идеи и идеальные формы лучше всего.

Математические концепции, такие как числа, геометрия и логика, предоставляют нам инструменты для анализа и понимания идеальных форм. Например, геометрия позволяет нам изучать идеальные геометрические фигуры, такие как круги и треугольники, которые существуют только в мире идеальных форм.

Важно подчеркнуть, что математика не исчерпывает все аспекты идеальных форм, но она предоставляет нам язык и инструменты для их изучения. Математические концепции помогают нам абстрагироваться от материального мира и погружаться в мир идеальных форм, где мы можем обнаружить гармонию, симметрию и идеальный порядок.

Таким образом, понятие идеальных форм и их связь с математическими концепциями показывают, что математика играет важную роль в познании и понимании мира идей и идеальных форм, и является неотъемлемой частью философии Платона.

Вклад Платона в развитие математической мысли и образования

Платон, великий древнегреческий философ, сыграл значительную роль в развитии математической мысли и образования. Его вклад в математику был огромным и оказал влияние на многие последующие поколения ученых и учеников.

Одним из важнейших достижений Платона в области математики является создание академии, первого высшего учебного заведения, в котором математика занимала центральное место. В академии Платона проводились занятия, на которых обсуждались различные математические теории и проводились исследования. Это стало отправной точкой для систематизации знаний и развития математической науки.

Платон также сформулировал идею о существовании математических истин, которые являются независимыми от нашего мира и существуют в форме идей. Он считал математику идеальным образом, позволяющим нам познавать истину и достигать познания о природе вселенной. Такие идеи оказали большое влияние на развитие математической мысли и способствовали появлению абстрактных математических концепций.

Еще одним важным вкладом Платона в образование является его учение о диалоге и искусстве ведения дискуссий. В своих диалогах Платон часто использовал математические примеры и аргументы, чтобы проиллюстрировать свои идеи и убедить своих слушателей. Это способствовало развитию критического мышления и способности анализировать и строить логические цепочки рассуждений.

В целом, вклад Платона в развитие математической мысли и образования нельзя переоценить. Его работы и идеи стали основой для многих последующих исследований и исследователей, и до сих пор оказывают влияние на современную математику и образование.

Вопрос-ответ:

Какую роль играет математика в философии Платона?

Математика занимает важное место в философии Платона, она является основой для понимания истины и реальности. Для Платона математика была главной наукой, которая позволяла нам познать сущность вещей и достичь истинного знания.

Почему Платон считал математику главной наукой?

Платон считал математику главной наукой, потому что она позволяет познать абсолютную истину и реальность. Для него математика была способом достичь познания идеальных форм, которые лежат в основе всего сущего.

Какие основные принципы математики Платон выделял?

Платон выделял несколько основных принципов математики. Во-первых, он считал, что математика исследует вечные идеи и формы, которые находятся за пределами нашего мира. Во-вторых, для Платона математика была средством достижения истины и познания абсолютных идей. И, наконец, Платон считал, что математика является основой для других наук и философии, так как она позволяет понять структуру мира и его законы.

Какое значение математика имеет в современной философии?

В современной философии математика имеет большое значение. Она является не только наукой, но и методом познания мира. Математика помогает развивать логическое мышление, абстрактное мышление и способность анализировать сложные проблемы. Она также играет важную роль в научных исследованиях и техническом прогрессе.

Какие принципы математики можно перенести на другие науки и философию?

Некоторые принципы математики, такие как логика, абстрактное мышление и анализ, могут быть перенесены на другие науки и философию. Например, логическое мышление и способность анализировать проблемы могут быть полезными при решении философских вопросов или проведении научных исследований. Абстрактное мышление также может помочь в понимании сложных концепций и идей.

Какую роль играет математика в философии Платона?

Математика играет ключевую роль в философии Платона. Он считал ее основой и ключом к пониманию реальности. Математика помогает нам познать идеальные формы, которые существуют вне нашего мира чувственного опыта.

Каким образом математика помогает нам познать идеальные формы?

Математика помогает нам познать идеальные формы, потому что она обладает абстрактным и логическим характером. Математические объекты, такие как числа и геометрические фигуры, существуют независимо от конкретных материальных объектов. Именно благодаря математике мы можем анализировать и понимать эти идеальные формы и открывать новые законы и отношения между ними.