Найдется это много где и в математике и в языке и даже у козьмы пруткова загадка
Содержимое
- 1 Найдется это много где и в математике и в языке и даже у козьмы пруткова загадка
- 1.1 Загадка у Козьмы Пруткова
- 1.2 Математика и язык: где найти сходство?
- 1.3 Поиск сходства
- 1.4 Математика и язык: две стороны одной медали
- 1.5 Правила и законы: основа математики и языка
- 1.6 Алгоритмы и грамматика: общие черты
- 1.7 Числа и слова: строительные блоки
- 1.8 Логика и смысл: ключевые компоненты
- 1.9 Знаки и звуки: общий язык
- 1.10 Поиск решений и построение предложений: общий процесс
- 1.11 Вопрос-ответ:
- 1.11.0.1 В чем состоит загадка у Козьмы Пруткова?
- 1.11.0.2 Какие примеры сходства между математикой и языком можно найти?
- 1.11.0.3 Как математика может помочь в изучении языка?
- 1.11.0.4 Как язык может помочь в изучении математики?
- 1.11.0.5 Каким образом сходство между математикой и языком может быть использовано в практических целях?
- 1.11.0.6 Какое сходство можно найти между математикой и языком?
- 1.12 Видео по теме:
Загадка с применением математики и языка, которую можно найти в различных источниках, включая книги и статьи. Расшифровка загадки Козьмы Пруткова.
Математика и язык — две разные области знания, которые кажутся несопоставимыми. Одна из них оперирует числами и формулами, а другая — словами и предложениями. Однако, Козьма Прутков утверждал, что существует некая загадочная точка пересечения между этими двумя науками.
При ближайшем рассмотрении становится ясно, что и математика, и язык имеют свои правила и структуру. В математике мы оперируем с логическими аксиомами, строим доказательства и рассуждения. Точно также и в языке мы используем грамматические правила, строим предложения и излагаем свои мысли.
Однако, особое сходство можно найти в области логических законов. В математике у нас есть аксиомы и правила вывода, которые мы используем для доказательства теорем. Также в языке мы имеем свои логические законы, такие как законы мышления и принципы логической связи.
Таким образом, можно сделать вывод, что математика и язык имеют общую основу — логику мышления. Обе науки оперируют логическими законами и правилами, которые помогают нам структурировать информацию и делать выводы. Это позволяет нам понять, почему Козьма Прутков говорил о сходстве между математикой и языком, ведь они оба основываются на логике и рациональности.
Загадка у Козьмы Пруткова
Козьма Прутков, вымышленный персонаж, оставил после себя множество афоризмов, загадок и шуток. Одна из его загадок посвящена сходству между математикой и языком.
Как известно, математика и язык являются двумя разными областями знаний, но при более внимательном рассмотрении можно найти между ними общие черты. Ведь и математика, и язык оперируют символами и правилами, используют логику и абстрактные понятия.
Математика имеет свою грамматику — алгебру, которая позволяет строить выражения и формулы, аналогично тому, как грамматика языка позволяет образовывать слова и предложения. Математические операции, такие как сложение, вычитание, умножение и деление, могут быть рассмотрены как аналоги грамматических правил, которые позволяют создавать новые выражения.
Кроме того, как и в языке, в математике существуют правила и конвенции, которые помогают установить единый смысл и понимание. Например, в языке существует правило согласования глагола с подлежащим, а в математике существуют правила приоритета операций.
И, наконец, как и в языке, где слова могут иметь различные значения в разных контекстах, в математике также могут быть разные интерпретации и применения одной и той же формулы или теоремы.
Таким образом, загадка Козьмы Пруткова указывает на то, что между математикой и языком существует сходство в использовании символов, правил и логики, хотя они и применяются в разных контекстах и областях знаний.
МатематикаЯзык
| Алгебра | Грамматика |
| Операции | Правила |
| Интерпретация | Контекст |
Математика и язык: где найти сходство?

Математика и язык, казалось бы, разные предметы. Однако, если внимательно посмотреть, можно заметить некоторые сходства между ними. Вот несколько точек соприкосновения:
- Логика. Как в математике, так и в языке используется логика. В математике мы строим доказательства на основе аксиом и правил вывода. В языке мы также используем логику, чтобы строить аргументы и доводы.
- Абстракция. В математике мы работаем с абстрактными понятиями, такими как числа, функции, пространства и т.д. Точно так же, в языке мы используем абстракции, чтобы выразить свои мысли и идеи.
- Структура. Как в математике, так и в языке имеется определенная структура. В математике мы работаем с формулами, уравнениями, графами и т.д. В языке мы также используем структуру, чтобы организовать свои высказывания и тексты.
- Точность. В математике требуется высокая степень точности и аккуратности. Точно так же, в языке мы должны быть точными и ясными, чтобы наши сообщения были понятными и не вызывали двусмысленности.
Это лишь некоторые примеры сходств между математикой и языком. Оба предмета требуют аналитического мышления, логического мышления и умения строить доказательства. Используя эти сходства, можно развивать свои навыки и в математике, и в языке одновременно.
Поиск сходства
Математика и язык, казалось бы, различные дисциплины, но при ближайшем рассмотрении можно найти некоторые сходства между ними.
Во-первых, и математика, и язык основаны на системах символов и правил, которые определяют их функционирование. В математике это числа, знаки операций и математические формулы, а в языке — буквы, звуки и грамматические правила.
Во-вторых, как и в математике, в языке существуют логические законы и правила. Например, в математике справедливо высказывание «если a=b и b=c, то a=c», а в языке существуют правила согласования слов по падежам и временам.
Кроме того, как и в математике, в языке можно проводить анализ и делать выводы. Например, по аналогии с математическими формулами, можно строить логические цепочки в предложениях и делать выводы на основе имеющейся информации.
Таким образом, можно сказать, что математика и язык имеют некоторые сходства в своей структуре и функционировании. Их изучение и применение позволяют нам лучше понимать мир и выражать свои мысли и идеи.
Математика и язык: две стороны одной медали
По сути, и математика, и язык являются системами символов и правил, которые используются для передачи информации. В математике символы – это числа, знаки и формулы, а правила – это математические операции и законы. В языке символы – это звуки, буквы и слова, а правила – это грамматика и синтаксис.
Кроме того, и математика, и язык имеют свою логику и структуру. Математика строится на строгих математических доказательствах и логических закономерностях. Язык также имеет свои правила и законы, которые определяют, как слова и фразы могут быть сочетаемыми.
Однако, самое главное сходство между математикой и языком заключается в том, что обе дисциплины позволяют нам описывать и анализировать мир вокруг нас. Математика помогает нам понять и предсказывать физические явления, решать задачи и строить модели. Язык позволяет нам общаться, передавать информацию и выражать свои мысли и чувства.
Таким образом, математика и язык – это две стороны одной медали, которые взаимосвязаны и взаимодействуют друг с другом. Они оба помогают нам понять и интерпретировать мир, в котором мы живем, и расширить наши познания и возможности.
Правила и законы: основа математики и языка
В математике существуют такие основополагающие понятия, как аксиомы, формулы и теоремы. Аксиомы задают базовые правила, которые не нуждаются в доказательстве. Формулы выражают математические отношения и связи. Теоремы же являются утверждениями, которые можно доказать на основе аксиом и других теорем.
Аналогично, в языке существуют грамматические правила, которые определяют порядок слов, образование форм и построение предложений. Также есть правила орфографии и пунктуации, которые регулируют написание и оформление текста. Использование этих правил позволяет передавать информацию точно и понятно.
Также как в математике, нарушение правил и законов в языке может привести к неправильному, незавершенному или недостаточно ясному выражению мысли. Правильное применение правил и законов в математике и языке позволяет достичь точности, ясности и понятности.
МатематикаЯзык
| Аксиомы | Грамматические правила |
| Формулы | Правила орфографии и пунктуации |
| Теоремы | Правила построения предложений |
Таким образом, правила и законы являются основой и фундаментом как для математики, так и для языка. Их соблюдение позволяет достичь точности, ясности и понятности в обоих случаях.
Алгоритмы и грамматика: общие черты
Алгоритмы — это последовательность шагов, которые должны быть выполнены для достижения определенной цели. Они используются в математике и информатике для решения различных задач. Алгоритмы имеют четкую структуру и строго определенные правила, по которым они выполняются.
Так же и грамматика — это система правил, которые определяют структуру и порядок слов и фраз в языке. Грамматика описывает, какие слова и каким образом могут быть скомбинированы, чтобы образовать правильные предложения. Она является основой для правильного построения предложений, анализа текста и общения на языке.
Как и алгоритмы, грамматика имеет строгую структуру и определенные правила, которые должны быть соблюдены. В обоих случаях важно точно следовать этим правилам, чтобы достичь желаемого результата.
Таким образом, можно сказать, что алгоритмы и грамматика имеют общие черты в виде строгой структуры и определенных правил. Это делает их важными инструментами в научных и практических областях, где требуется точность и последовательность действий.
Числа и слова: строительные блоки
Числа являются основой математики. Они позволяют нам измерять, считать, сравнивать и решать различные задачи. В математике используются различные типы чисел: натуральные, целые, рациональные, иррациональные и дробные. Каждое число имеет свою уникальную характеристику и свойство.
Слова, с другой стороны, позволяют нам описывать мир и общаться с другими людьми. С помощью слов мы передаем информацию, выражаем свои мысли и чувства. Слова могут быть объединены в предложения, а предложения – в тексты. Каждое слово имеет свое значение и функцию в языке.
Как и числа, слова имеют свои правила и законы. Они могут быть объединены в группы по разным признакам: по части речи, по смыслу, по грамматическим характеристикам и т.д.
Кроме того, как числа, так и слова могут быть использованы для создания различных структур. Например, числа могут быть объединены в алгебраические формулы или матрицы, а слова – в предложения или стихи. В обоих случаях, правильное сочетание чисел или слов важно для достижения определенной цели.
Таким образом, числа и слова являются не только строительными блоками, но и инструментами, которые помогают нам познавать и описывать мир вокруг нас. Они обладают своими уникальными свойствами и правилами использования, которые необходимо изучать и понимать, чтобы глубже понять их значение.
Логика и смысл: ключевые компоненты
Логика — это наука, изучающая правила заключения и вывода. В математике она используется для доказательства теорем и построения строгих математических доводов. В языке логика помогает нам строить правильные и понятные предложения, аргументировать свои мысли и избегать логических ошибок.
Другой важной компонентой, объединяющей математику и язык, является смысл. В математике и языке смысл играет ключевую роль и определяет, как правильно и понятно сформулировать высказывание, формулу или уравнение. Чтобы понять и применять математические концепции, необходимо понять их смысл. То же самое относится и к языку — чтобы правильно использовать слова и фразы, необходимо понимать их значения и смысловые оттенки.
Таким образом, логика и смысл являются ключевыми компонентами, объединяющими математику и язык. Они помогают нам строить логически верные высказывания и понятно формулировать мысли. Их понимание и использование являются основой успешного изучения и применения как математики, так и языка.
Знаки и звуки: общий язык

В языке мы используем звуки, буквы и слова для общения и передачи мыслей. Аналогично, в математике мы используем математические знаки, символы и формулы для выражения математических идей и отношений.
Оба языка имеют свою грамматику и правила. Например, в языке есть грамматические правила, определяющие порядок слов в предложении и образование форм слов. В математике также есть правила, определяющие порядок операций и использование символов.
Кроме того, оба языка могут быть использованы для описания и анализа мира вокруг нас. Например, в языке мы можем описывать предметы, события и отношения между ними. В математике мы можем описывать физические явления, экономические процессы и социальные взаимодействия.
Таким образом, хотя математика и язык — разные области знания, они оба используют знаки и звуки для передачи информации и имеют общие черты в своей структуре и функциональности.
Поиск решений и построение предложений: общий процесс

Процесс поиска решений в математике начинается с анализа задачи и определения неизвестных величин. Затем проводится работа с известными данными, применяются специальные методы и алгоритмы для получения результата. В конце процесса осуществляется проверка полученного решения на корректность и правильность.
В языке процесс построения предложений начинается с формулирования идеи или мысли, которую необходимо выразить. Затем выбираются подходящие слова и выражения, которые помогут передать задуманное. Далее следует работа с грамматикой и синтаксисом языка, для правильного оформления предложения. В конце процесса осуществляется проверка созданного предложения на связность и понятность для других людей.
Оба процесса требуют логического мышления, умения анализировать информацию и применять специальные правила и методы. В математике это математические операции, формулы и теоремы, а в языке — правила грамматики, синтаксиса и стилистики.
Таким образом, можно сказать, что поиск решений в математике и построение предложений в языке имеют сходство в общем процессе выполнения задачи. Они требуют систематического подхода, последовательности действий и умения применять специальные правила и методы для достижения конечного результата.
Вопрос-ответ:
В чем состоит загадка у Козьмы Пруткова?
Загадка у Козьмы Пруткова заключается в поиске сходства между математикой и языком.
Какие примеры сходства между математикой и языком можно найти?
Одним из примеров сходства между математикой и языком может быть использование логических операций и алгоритмов при решении языковых задач.
Как математика может помочь в изучении языка?
Математика может помочь в изучении языка, так как она развивает логическое мышление и аналитические способности, что полезно при изучении грамматики и синтаксиса языка.
Как язык может помочь в изучении математики?
Язык может помочь в изучении математики, так как формулирование математических задач и объяснение математических концепций требуют хорошего языкового навыка и ясности выражения мыслей.
Каким образом сходство между математикой и языком может быть использовано в практических целях?
Сходство между математикой и языком может быть использовано для разработки компьютерных программ, которые могут анализировать и обрабатывать естественный язык, а также для создания систем автоматического перевода и распознавания речи.
Какое сходство можно найти между математикой и языком?
Между математикой и языком есть несколько сходств. Во-первых, оба предмета имеют свои правила и законы. Как в математике, так и в языке есть определенные правила, которые нужно соблюдать, чтобы получить верный результат. Во-вторых, и математика, и язык используют символы и символьные выражения. В математике это числа, переменные и операции, а в языке — буквы и слова. Кроме того, и математика, и язык позволяют описывать и анализировать различные явления и процессы.


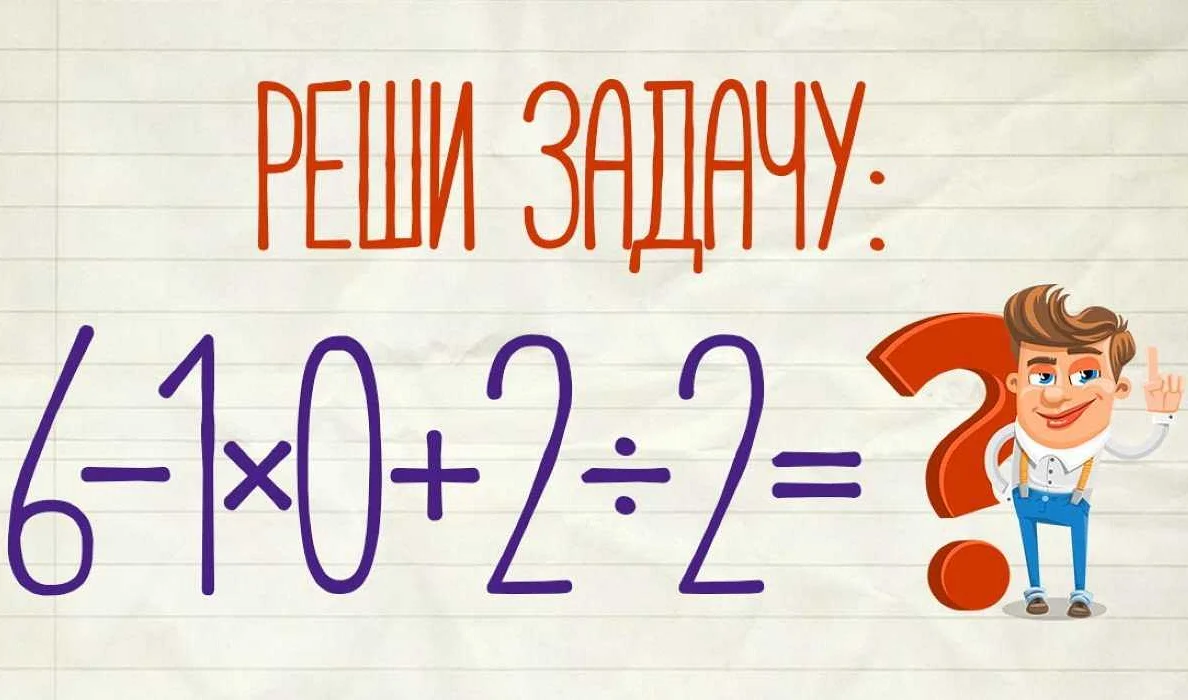

Статья привлекает внимание заголовком и удерживает интерес содержанием. Прутков, известный своими загадками и афоризмами, предлагает новый взгляд на взаимосвязь математики и языка. Чтение статьи вызывает у меня любопытство, и я с нетерпением ожидаю обнаружения сходства между этими двумя на первый взгляд непохожими областями. Автор начинает статью с определения математики и языка, подчеркивая их важность для человечества. Он указывает на то, что оба этих предмета основаны на системах и правилах, которые позволяют нам описывать и понимать мир вокруг нас. Я думаю, что это правда, так как и математика, и язык являются универсальными средствами коммуникации и позволяют нам выражать свои мысли и идеи. Далее автор предлагает несколько примеров, которые подтверждают сходство между математикой и языком. Он упоминает, что и та, и другая область требуют точности и логики в использовании символов и правил. Прутков говорит о том, что как и язык, математика используется для решения различных задач и построения аргументаций. Читая статью, я начинаю осознавать, что математика и язык имеют много общего. Оба они являются способами структурирования и описания информации. Математика помогает нам анализировать и понимать миры чисел и формул, а язык — выражать идеи и чувства через слова и предложения. В заключение, статья Козьмы Пруткова о сходстве между математикой и языком является захватывающей и интересной. Она позволяет нам увидеть, что эти две области имеют глубокое взаимодействие и влияют друг на друга. Я рада, что прочитала эту статью, она расширила мое понимание математики и языка.
Статья очень интересная и полезная. Математика и язык, казалось бы, разные по своей природе, но вдумчиво прочитав статью, я поняла, что они имеют некоторое сходство. Оба предмета требуют точности, логики и систематического подхода. Как и в математике, в языке существуют определенные правила и законы, которые нужно усвоить для понимания его структуры. Математика и язык также основаны на символах и символических операциях. Кроме того, как и в математике, в языке есть понятия «правильное» и «неправильное», «логичное» и «нелогичное». Математика и язык оба являются мощными инструментами для выражения мыслей и идей. В обоих случаях важно быть ясным, последовательным и точным. Приятно осознавать, что эти два разных предмета так тесно связаны, и понимание этого помогает лучше понять и использовать оба. Спасибо автору за такую интересную и познавательную статью!
В статье «Загадка у Козьмы Пруткова: где можно найти сходство между математикой и языком?» автор предлагает нам заглянуть в мир математики и языка, чтобы найти неожиданные сходства между этими двумя областями знаний. Как женщина, я сразу заинтересовалась этой темой, ведь математика и язык — это две сферы, которые, казалось бы, не имеют ничего общего. Однако, благодаря статье я поняла, что обе эти области тесно связаны и взаимодействуют друг с другом. Автор приводит примеры, которые показывают, что математика и язык имеют много общих черт. Например, оба предмета базируются на правилах и законах. В математике мы работаем с числами, формулами, алгоритмами, а в языке — с грамматикой, правописанием, синтаксисом. В обоих случаях существует логика и последовательность действий, которые помогают нам понять и использовать эти знания. Одно из самых интересных сходств, которое я обнаружила, это использование символов и символики. В математике мы работаем с числами и знаками, такими как +, -, *, / и т.д. В языке мы также используем буквы, знаки препинания и другие символы, чтобы передать свои мысли и идеи. Оба предмета имеют свою уникальную систему символов, которая позволяет нам выражать наши мысли и коммуницировать с другими людьми. Также, автор обращает внимание на стройность и точность, которые являются общими чертами и для математики, и для языка. В математике невозможно допустить ошибку или неточность, каждый шаг должен быть обоснован и точно вычислен. Точно так же и в языке каждое слово, каждая фраза должны иметь свою логическую связь и смысл. Мы должны быть аккуратными в выборе слов, чтобы передать наши мысли и идеи с максимальной ясностью. В целом, статья дает нам возможность заглянуть в мир математики и языка и обнаружить их неожиданные сходства. Я убедилась, что эти две области знаний имеют глубокие корни исходя из одной и той же логики и законов. Математика и язык — это неотъемлемые части нашей жизни, которые помогают нам понимать и описывать мир вокруг нас.