Что такое зет в математике

Зет в математике – это математическая функция, которая используется для вычисления сумм бесконечных рядов. Она имеет важное значение в анализе, комбинаторике и теории чисел. Узнайте, как работает функция зет и как ее применяют в различных математических задачах.

В математике зет — это математическое обозначение, которое используется для обозначения некоторых важных параметров или переменных в различных областях математики. Зет может представлять собой конкретное число, функцию или символ, зависящий от контекста, в котором он используется.

Одно из самых известных применений зет в математике — это использование символа зет для обозначения целых чисел или множества целых чисел. Например, символ зет может быть использован для обозначения множества всех целых чисел или множества положительных целых чисел.

Зет также может быть использован для обозначения суммы или накопления некоторой величины. Например, символ зет может быть использован для обозначения суммы ряда чисел или суммы всех элементов вектора.

Зет также может иметь специальное значение в некоторых областях математики, таких как теория вероятностей и теория чисел. В теории вероятностей зет может обозначать функцию распределения или вероятность события. В теории чисел зет может обозначать функцию Римана, которая имеет важное значение в анализе простых чисел.

В заключение, зет в математике является универсальным символом, который может использоваться для обозначения различных математических понятий и операций. Зет обладает свойствами, которые зависят от контекста, в котором он используется, и может иметь различные значения в разных областях математики.

Определение зет в математике

Зет можно представить как бесконечную последовательность чисел: … -3, -2, -1, 0, 1, 2, 3, …

Целые числа являются расширением натуральных чисел, которые включают только положительные числа, и добавляют отрицательные числа и ноль. Зет используется для решения различных математических задач, в том числе в алгебре, арифметике, комбинаторике и других областях математики.

Зет обладает рядом свойств, которые определяют его особенности и позволяют проводить операции с целыми числами. Например, зет является замкнутым относительно сложения и вычитания — если сложить или вычесть два целых числа, то результат также будет целым числом.

Видео по теме:

Свойства зет в математике

1. Коммутативность:

Свойство зет называется коммутативным, если для любых двух чисел a и b выполняется равенство z(a, b) = z(b, a). Иными словами, результат зет-операции не зависит от порядка чисел.

2. Ассоциативность:

Свойство зет называется ассоциативным, если для любых трех чисел a, b и c выполняется равенство z(a, z(b, c)) = z(z(a, b), c). Это означает, что результат зет-операции не зависит от расстановки скобок.

3. Нейтральный элемент:

Существует такое число e, что для любого числа a выполняется равенство z(a, e) = a и z(e, a) = a. Число e называется нейтральным элементом зет-операции.

4. Обратный элемент:

Для каждого числа a существует такое число b, что z(a, b) = e и z(b, a) = e, где e — нейтральный элемент. Число b называется обратным элементом к числу a относительно зет-операции.

5. Дистрибутивность:

Зет-операция обладает свойством дистрибутивности относительно другой операции, если для любых трех чисел a, b и c выполняется равенство z(a, (b + c)) = z(a, b) + z(a, c) и z((a + b), c) = z(a, c) + z(b, c), где + обозначает другую операцию.

6. Уникальность нейтрального элемента:

В зет-операции может существовать только одно число, которое является нейтральным элементом.

Примеры использования зет в математике

Одним из примеров использования зет является запись суммы чисел от 1 до n. Например, зет от i равно 1 до n i обозначает сумму всех чисел от 1 до n: ∑i=1n i = 1 + 2 + 3 + … + n.

Зет также часто используется для вычисления суммы ряда. Например, зет от n равно 1 до бесконечности 1/n2 обозначает сумму всех чисел 1/n2 при n, пробегающем все натуральные числа от 1 до бесконечности.

В математических формулах зет может быть использован для вычисления суммы произвольного количества членов ряда или последовательности. Например, зетi=1n ai обозначает сумму всех элементов ai от i равно 1 до n.

Таким образом, зет является мощным инструментом математической нотации и позволяет удобно записывать и вычислять суммы чисел в различных математических задачах.

Зет в алгебре

Формула комплексного числа обычно записывается в виде z = a + bi, где a — вещественная часть, b — мнимая часть, а i — мнимая единица. Здесь зет (ζ) используется для обозначения комплексного числа в общем виде.

Комплексные числа с помощью зет могут быть представлены в виде точек на комплексной плоскости, где вещественная часть числа отображается по горизонтальной оси, а мнимая часть — по вертикальной оси. Такая геометрическая интерпретация комплексных чисел помогает в решении различных математических задач, включая решение уравнений и графиков функций.

Зет также применяется в алгебре для обозначения функции зет-функции (ζ-функции). Эта функция имеет множество математических свойств и широкий спектр приложений, включая теорию чисел и теорию вероятностей.

СвойствоОписание

Симметрия	Зет-функция удовлетворяет функциональному уравнению, которое обеспечивает симметрию функции относительно линии Re(s) = 1/2.
Аналитическое продолжение	Зет-функция может быть аналитически продолжена на всю комплексную плоскость, за исключением s = 1, где функция имеет полюс.
Теорема Эйлера	Зет-функция связана с бесконечным произведением, известным как Теорема Эйлера, которая устанавливает связь между простыми числами и их степенными суммами.

Зет в геометрии

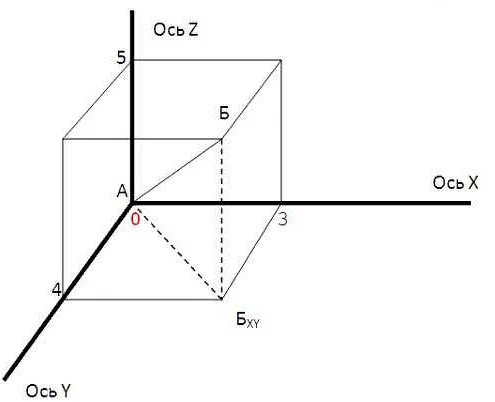
В геометрии зет (Z) представляет собой одну из важных фигур, которая образуется пересечением двух прямых. Зет обладает рядом особенностей и свойств, которые делают ее полезным инструментом в геометрии.

Свойства зет в геометрии:

Пересечение прямых	Зет образуется при пересечении двух прямых, несмотря на углы их взаимного расположения.
Углы зет	Углы зет могут быть прямыми (90°), острыми (90°), в зависимости от углов, образованных пересечением прямых.
Симметричность	Зет является симметричной фигурой, то есть ее левая и правая половины совпадают.
Угловая сумма	Сумма углов зет всегда равна 360°.
Использование зет	Зет часто используется в геометрии для обозначения пересечения двух прямых, а также в различных теоремах и задачах.

Примеры использования зет в геометрии могут включать построение и измерение углов, нахождение точек пересечения прямых и решение геометрических задач, связанных с пересечением прямых и углами.

Зет в теории чисел

Зет-функция Римана обозначается символом ζ(s). Определение этой функции выглядит следующим образом:

ζ(s) = 1^s + 2^s + 3^s + 4^s + …

Данное определение имеет смысл только при условии, что вещественная часть числа s больше единицы. В противном случае, ряд справа расходится. Однако, с помощью методов аналитической продолжаемости, зет-функция может быть определена и для других значений s, включая отрицательные и даже комплексные числа.

Важным свойством зет-функции является симметрия, известная как функциональное уравнение Римана:

ζ(s) = 2^s * π^(s-1) * sin(πs/2) * Г(1-s) * ζ(1-s)

где Г(1-s) — гамма-функция, π — число пи, а sin(πs/2) — синус комплексного числа.

Зет-функция Римана имеет множество интересных свойств и применений в теории чисел. Она тесно связана с распределением простых чисел и представлением целых чисел в виде сумм кубов, квадратов и др. Также зет-функция используется в теории вероятности, криптографии и физике.

Зет в математическом анализе

Зет в математическом анализе имеет несколько свойств:

1. Множество целых чисел является бесконечным и несчетным.
2. Целые числа можно складывать, вычитать и умножать между собой.
3. Множество целых чисел обладает порядком: для любых двух целых чисел a и b, либо a > b, либо a < b, либо a = b.
4. Множество целых чисел не обладает операцией деления с остатком.

Зет применяется в математическом анализе для решения различных задач, связанных с целыми числами. Он используется, например, при изучении рядов и последовательностей, а также при решении уравнений и неравенств. Множество целых чисел является важной основой для построения других числовых множеств, таких как рациональные и вещественные числа.

В заключение, зет в математическом анализе – это обозначение для множества целых чисел, которое играет важную роль во многих математических разделах. Знание свойств и применение зет позволяет решать различные задачи, связанные с целыми числами.

Вопрос-ответ:

Что такое зет в математике?

Зет (или зед) — это греческая буква, обозначающая в математике и физике сумму бесконечного ряда. В математической нотации зет часто используется для обозначения суммы последовательности чисел или функций.

Какие свойства имеет зет в математике?

Зет обладает несколькими свойствами. Одно из них — замена индекса суммирования. То есть, если суммировать по переменной i, то замена i на j в пределе суммирования не меняет значения суммы. Также, зет обладает свойством линейности, то есть сумма двух зет равна зет суммы. Кроме того, зет может использоваться для обозначения бесконечной суммы, которая может иметь как конечное, так и бесконечное значение.

В каких областях математики используется зет?

Зет широко используется в различных областях математики. Например, в теории вероятностей зет используется для вычисления вероятности событий. В анализе зет может быть использован для вычисления определенных интегралов. Также, в комбинаторике зет может быть использован для вычисления количества комбинаций или перестановок. Это лишь некоторые примеры использования зет в математике.

Можно ли использовать зет для суммирования дробей?

Да, зет можно использовать для суммирования дробей. В таком случае зет будет обозначать сумму последовательности дробей. Например, если есть последовательность дробей 1/2, 1/4, 1/8 и т.д., то их сумму можно записать с помощью зет: зет(i=1 до бесконечности) 1/2^i. Это позволяет удобно вычислить значение суммы дробей.