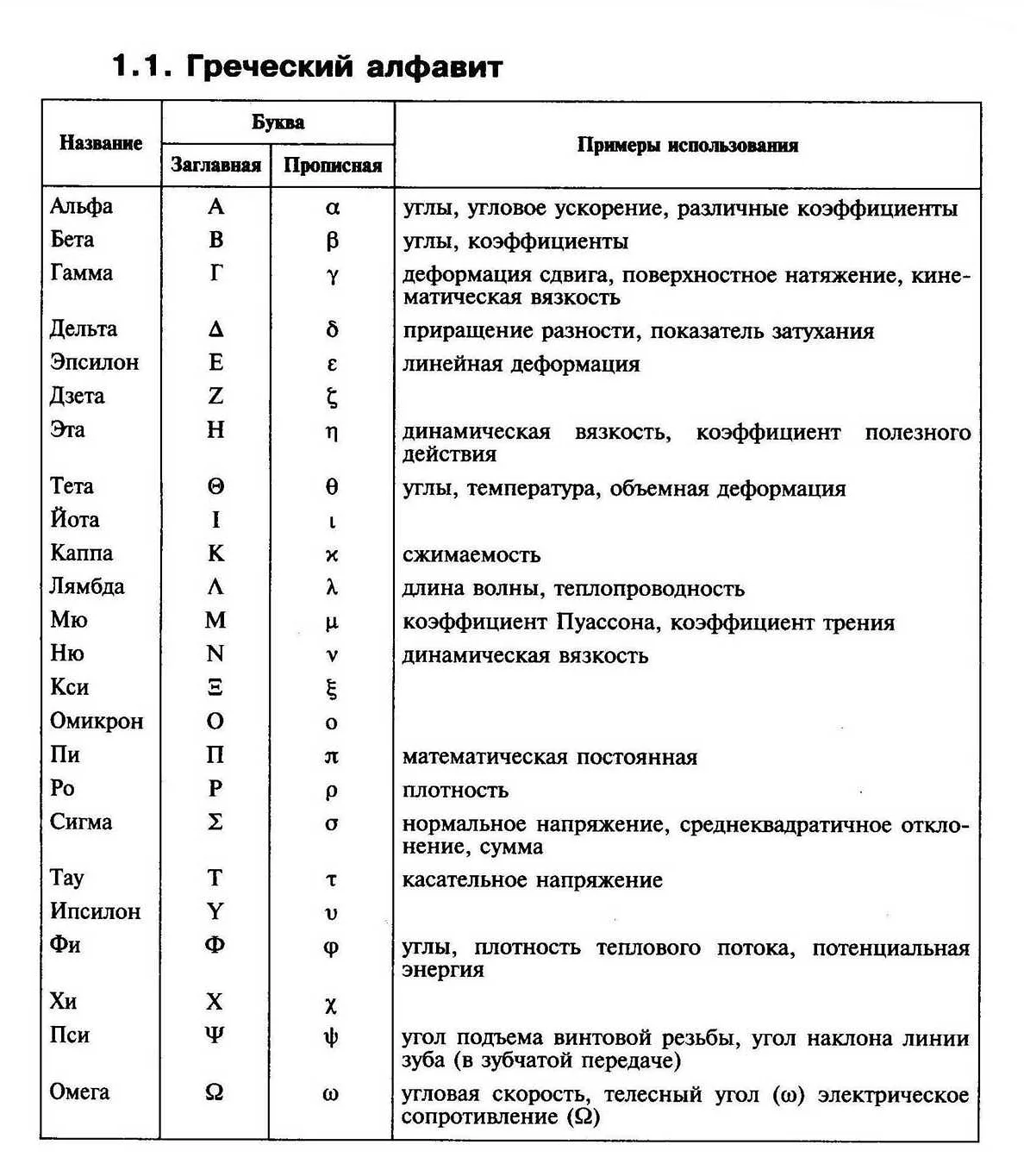
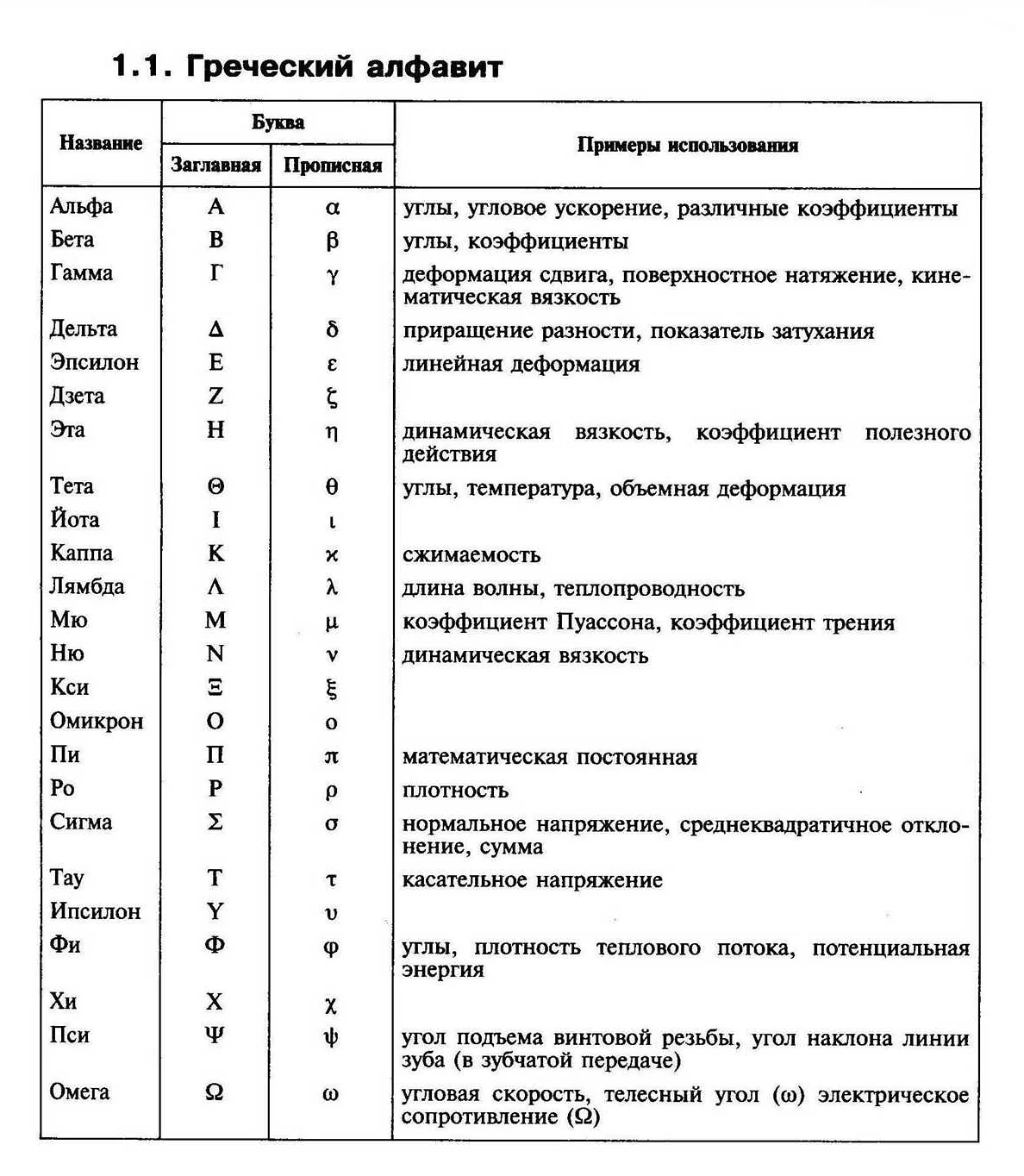
Что обозначает кси в математике

Кси (ξ) — символ греческого алфавита, который используется в математике для обозначения различных величин или переменных. Узнайте, как кси применяется в различных областях математики и как его можно интерпретировать.

Кси (ξ) – греческая буква, которая имеет особое значение в математике. Она используется для обозначения различных величин и понятий в разных областях науки. У греческой буквы кси есть несколько вариантов написания: строчная (ξ) и заглавная (Ξ).

В математике кси может обозначать различные величины, например, показатель степени, координату или значение величины. Она также широко используется в статистике, теории вероятности, теории множеств и других областях математики.

Примером использования кси в математике может быть обозначение показателя степени. Например, если у нас есть выражение x^2, то x – это переменная, а 2 – показатель степени. В этом случае кси обозначает показатель степени и указывает на то, что переменная x возводится во вторую степень.

В статистике кси может обозначать стандартное отклонение или случайную величину. В теории вероятности кси может использоваться для обозначения случайной величины или плотности распределения. В теории множеств кси может обозначать элемент множества или функцию.

Таким образом, кси играет важную роль в математике и используется для обозначения различных понятий и величин. Понимание значения кси позволяет более глубоко осмыслить и изучить различные математические концепции и теории.

Кси в математике: основные понятия и примеры использования

Основные понятия

Кси может быть использовано для обозначения различных величин и функций. В теории вероятности и статистике, кси может обозначать случайную величину или ее функцию распределения. Например, если ξ — случайная величина, то F(ξ) может обозначать функцию распределения этой случайной величины.

В математической физике кси может использоваться для обозначения координаты в пространстве. Например, если (ξ, η, ζ) — трехмерные координаты, то ξ может обозначать координату по оси X.

Примеры использования

• В теории вероятности и статистике, кси может использоваться для обозначения случайной величины. Например, ξ может быть равно количеству выпавших шестерок при броске кубика.
• В математической физике кси может использоваться для обозначения координаты точки в пространстве. Например, (ξ, η, ζ) может обозначать координаты точки в трехмерном пространстве.
• В теории графов, кси может использоваться для обозначения вершины графа. Например, если G = (V, E) — граф, то ξ может обозначать вершину этого графа.

Это лишь некоторые примеры использования кси в математике. Он широко применяется и имеет множество различных интерпретаций в разных областях математики.

Значение символа кси

В математическом анализе кси может обозначать независимую переменную или аргумент функции. Например, в уравнении f(ξ) = ξ2 + 2ξ — 5, кси представляет собой независимую переменную, которая может принимать различные значения.

Кси также широко используется в статистике для обозначения выборочного среднего. Например, ξ может быть использовано для обозначения среднего значения выборки X1, X2, …, Xn.

В линейной алгебре кси может использоваться для обозначения неизвестных коэффициентов в системе линейных уравнений. Например, в системе уравнений:

• 2ξ + 3γ = 5
• 4ξ — γ = 2

ξ и γ могут обозначать неизвестные значения, которые нужно найти.

Также кси может использоваться в различных областях математики и физики для обозначения других величин, параметров или переменных. Значение символа кси зависит от контекста и области применения.

Кси в алгебре

В алгебре кси (ξ) часто используется для обозначения неизвестной переменной или корня уравнения. Кси может быть использована в различных областях алгебры, от линейной до абстрактной.

Пример использования кси в алгебре:

УравнениеРешение

2ξ + 5 = 11	ξ = 3
ξ^2 + 4ξ + 4 = 0	ξ = -2

В первом примере кси используется для нахождения значения переменной, удовлетворяющей уравнению. Во втором примере кси используется для обозначения корня квадратного уравнения.

Использование кси в алгебре позволяет более компактно записывать уравнения и проводить вычисления, основываясь на свойствах алгебры и арифметики.

Кси в геометрии

В геометрии символ кси (ξ) используется для обозначения различных величин и понятий. Он может обозначать координату, расстояние, угол или другие геометрические характеристики.

Один из примеров использования символа кси в геометрии — это обозначение неизвестной координаты в системе координат. Например, в декартовой системе координат (x, y) символ кси может использоваться для обозначения неизвестной координаты по оси x.

Кси также может использоваться для обозначения расстояния между двумя точками. Например, если A и B — две точки на плоскости, то расстояние между ними можно обозначить как ξ = AB.

Другим примером использования символа кси в геометрии является обозначение угла. Например, если у нас есть треугольник ABC, то угол BAC можно обозначить как ξ = ∠BAC.

Таким образом, символ кси играет важную роль в геометрии, обозначая различные геометрические величины и понятия. Его использование помогает упростить запись и анализ геометрических задач.

Примеры использования кси в математических формулах

1. Система уравнений:

ξ1x + ξ2y + ξ3z = ξ4

ξ5x + ξ6y + ξ7z = ξ8

ξ9x + ξ10y + ξ11z = ξ12

Здесь ξ1, ξ2, ξ3, ξ4, ξ5, ξ6, ξ7, ξ8, ξ9, ξ10, ξ11 и ξ12 — это коэффициенты, которые могут принимать различные значения в зависимости от условий задачи.

2. Функция:

f(ξ) = ξ^2 + ξ + 1

В данном примере ξ используется для обозначения аргумента функции. Произвольное значение ξ приведет к определенному значению функции f(ξ).

3. Вероятность:

P(ξ > a) = 1 — P(ξ < a)

Здесь ξ — случайная величина, а a — некоторое число. Вероятность P(ξ > a) равна единице минус вероятность P(ξ < a).

4. Теория вероятностей:

ξ ~ N(μ, σ^2)

В данном примере ξ обозначает случайную величину, которая распределена по нормальному закону с параметрами μ (математическое ожидание) и σ^2 (дисперсия).

Это лишь некоторые примеры использования кси в математических формулах. В общем случае, кси используется для обозначения различных величин и параметров в различных областях математики.

Кси в теории вероятностей

В теории вероятностей символ «кси» (ξ) часто используется для обозначения случайной величины или набора случайных величин. Случайные величины могут иметь различные значения в зависимости от исхода случайного эксперимента, поэтому кси представляет собой математическую переменную, которая может принимать разные значения с определенными вероятностями.

Кси в теории вероятностей может быть как дискретной, так и непрерывной случайной величиной. В случае дискретной случайной величины кси может принимать только конечное или счетное количество значений. Например, при подбрасывании монеты кси может принимать значения «орел» или «решка». В случае непрерывной случайной величины кси может принимать любое значение в определенном диапазоне. Например, при измерении времени выполнения задачи кси может принимать любое положительное число.

Кси используется для описания различных вероятностных распределений, таких как биномиальное распределение, нормальное распределение, экспоненциальное распределение и другие. Кси может быть использована для расчета вероятностей событий, оценки статистических показателей, построения графиков и т.д.

В теории вероятностей кси играет важную роль, так как позволяет формализовать случайные явления и проводить математические операции над ними. Кси позволяет решать широкий класс задач, связанных с анализом вероятностей и статистикой.

Кси в дифференциальных уравнениях

Для примера рассмотрим однородное линейное дифференциальное уравнение второго порядка:

a1(x)y» + a0(x)y’ + a2(x)y = 0

где y» — это вторая производная функции y по переменной x, y’ — это первая производная функции y по переменной x, а a0(x), a1(x), a2(x) — это коэффициенты, зависящие от переменной x.

С помощью параметра кси можно привести это уравнение к каноническому виду:

y» + p(x)y’ + q(x)y = 0

где p(x) и q(x) — это новые функции, зависящие от переменной x.

Для этого параметра существует формула преобразования:

x = x(ξ)

y(x) = u(ξ)

причем p(x) и q(x) могут быть выражены через производные по ξ:

p(x) = p(ξ)(dξ/dx)^2 + r(ξ)d^2ξ/dx^2

q(x) = q(ξ)

где r(ξ) — это производная p(ξ) по ξ.

Использование параметра кси позволяет упростить решение дифференциальных уравнений и найти аналитическое решение в случаях, когда прямое интегрирование или другие методы неэффективны.

Кси в статистике

В статистике значение кси, обозначаемое как χ (греческая буква кси), часто используется для оценки соответствия между наблюдаемыми и ожидаемыми значениями в рамках различных статистических тестов.

Одним из основных примеров использования кси в статистике является критерий χ2 Пирсона. Этот критерий позволяет определить статистическую значимость различий между наблюдаемыми и ожидаемыми значениями в таблице сопряженности. Значение χ2 рассчитывается путем сравнения фактического распределения значений с ожидаемым распределением по определенному статистическому закону.

Другим примером использования кси в статистике является критерий адекватности модели. Данный критерий позволяет оценить, насколько хорошо модель соответствует наблюдаемым данным. Значение χ в данном случае рассчитывается путем сравнения наблюдаемых значений с предсказанными значениями модели.

Общая идея использования кси в статистике заключается в том, чтобы определить, насколько хорошо наблюдаемые данные соответствуют ожидаемым значениям или предсказанным моделью значениям. Чем больше значение χ, тем меньше соответствие между данными и ожидаемыми/предсказанными значениями.

Таким образом, кси играет важную роль в статистике и является одним из ключевых показателей для оценки статистической значимости различий и адекватности моделей.

Значение кси в других областях математики

В теории вероятности и статистике, кси может обозначать случайную величину или нормальное распределение. Например, кси может быть использована для обозначения случайной величины, представляющей количество успехов в серии независимых испытаний.

Кси также может обозначать относительную частоту, которая является мерой вероятности события. Это понятие используется в статистике для оценки вероятности событий на основе наблюдаемых данных.

В математическом анализе и дифференциальных уравнениях, кси может обозначать независимую переменную или переменную преобразования. Например, кси может быть использована для обозначения переменной, представляющей время или пространственную координату в уравнении.

Кси также может быть использована для обозначения функций и операций. Например, кси может быть использована для обозначения функции распределения или характеристической функции. Кроме того, кси может быть использована для обозначения операции суммирования или произведения.

В общем, значение кси в математике может варьироваться в зависимости от контекста и области применения. Это обозначение является удобным и стандартным способом обозначения переменных и функций, что позволяет упростить математические выражения и формулы.

Вопрос-ответ:

Зачем нужно знать значение кси в математике?

Знание значения кси в математике позволяет решать различные задачи и проблемы, связанные с анализом функций, определением экстремумов, нахождением корней уравнений и т.д. Оно является ключевым понятием в математическом анализе и алгебре.

Каково значение кси в математике?

Значение кси в математике обычно обозначает некоторую переменную или неизвестное число. Оно может быть любым числовым значением, в зависимости от контекста задачи или уравнения, в котором используется символ кси.

Приведите примеры использования кси в математике.

Кси может использоваться в различных математических областях. Например, в алгебре, кси может быть переменной, обозначающей неизвестное число. В анализе функций, кси может быть использовано для обозначения независимой переменной. Также кси может быть использовано в статистике для обозначения случайной величины или параметра распределения.

Какая связь между кси и другими математическими понятиями?

Кси может быть связано с другими математическими понятиями в зависимости от контекста. Например, в анализе функций, кси может быть связано с понятием производной или экстремума. В алгебре, кси может быть связано с уравнениями и системами уравнений. Связь кси с другими понятиями определяется конкретной математической задачей или теорией, в которой оно используется.

Видео по теме: