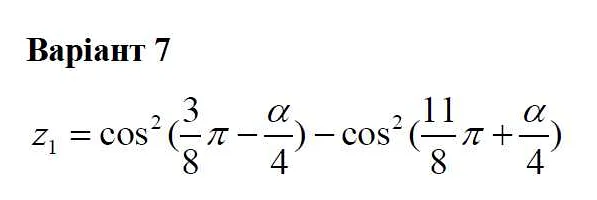Знаковая форма представления математической информации: основные принципы и примеры

В статье рассматривается знаковая форма представления математической информации, которую можно найти в учебниках, научных статьях и других материалах по математике. Речь идет об использовании математических символов, формул, таблиц и графиков, которые помогают наглядно представить и структурировать математические концепции и данные.

Существует множество способов представления математической информации, от ручной записи на бумаге до использования программных средств. Однако очень важно понимать, что в процессе представления математической информации мы должны иметь дело с знаками и символами, которые не менее важны, чем сами числа или формулы. Поэтому рассмотрение знаковых форм, используемых для представления математической информации, является ключевым вопросом.

Использование знаковых форм в математике имеет долгую историю и связано с развитием языка математики. Благодаря использованию знаков и символов были созданы удобные и компактные способы записи математических формул и выражений, что значительно ускорило развитие математики как науки. Сейчас существуют различные стандарты и соглашения относительно того, какие знаки и символы следует использовать при представлении математической информации.

В данной статье мы рассмотрим основные концепции знаковых форм для представления математической информации, такие как различные типы знаков и символов, их назначение, а также способы использования знаковых форм при записи математических выражений разного уровня сложности.

Знаковые формы для представления математической информации

Математическая информация является важным компонентом в образовании и научной деятельности. Для ее представления используются знаковые формы, такие как символы, формулы, графики и таблицы. Каждая из этих форм имеет свои особенности и используется в зависимости от задачи и контекста.

Символы — это основные знаки, которые используются в математике для обозначения чисел, операций, функций и переменных. Кроме того, символы могут использоваться для обозначения констант, единиц измерения, математических операций и многого другого. Символы имеют строгую систему правил и стандартов использования, что позволяет избежать недопонимания при коммуникации и обмене информацией.

Формулы — это математические выражения, которые состоят из символов и определяют отношения между числами и переменными. Формулы могут быть простыми или сложными, и их использование позволяет более точно и компактно выражать математические концепции и идеи. Формулы часто используются в научных и технических документах, статьях и книгах.

Графики — это знаковые формы, которые позволяют визуально представить данные или математические концепции. Графики могут иметь различные формы, такие как линейные, круговые, столбчатые и т.д. Они могут отображать изменения величин, зависимости между переменными или распределение данных. Графики используются не только в математике, но и в физике, биологии, экономике и других научных областях.

Таблицы — это структурированные формы, которые позволяют представить большое количество числовых данных и информации. Таблицы могут быть использованы для сравнения данных, суммирования значений, определения зависимости между переменными и т.д. Таблицы могут быть представлены в различных форматах, таких как Excel, CSV, HTML и другие.

В целом, знаковые формы являются неотъемлемой частью математической информации и позволяют удобно и эффективно ее представлять и передавать.

Что такое знаковые формы?

Знаковые формы – это способы представления математической информации, которые используются для передачи знаний о математических объектах и отношениях. Эти формы могут включать в себя символы, числа, графики, диаграммы, таблицы и другие способы визуального представления математической информации.

Важной особенностью знаковых форм является то, что они могут быть универсальными и применяться в различных культурах и языках, не завися от конкретной лексической формы. Например, знак “+” может быть понятен в любой стране, даже если название операции “сложение” будет написано на другом языке.

Знаковые формы широко используются в математическом образовании для облегчения понимания материала студентами и улучшения коммуникации между математиками. Они также могут быть полезны для визуализации данных в различных научных дисциплинах, где математика играет важную роль.

Знаковые формы являются неотъемлемой частью современной математики и продолжают развиваться и улучшаться в соответствии с потребностями современных исследований. Их использование помогает не только лучше понимать математические концепции, но и создавать новые идеи и решения.

Знаковые системы

Знаковая система — это система, с помощью которой передаются сообщения, представленные в виде знаков. Знаком может быть буква, слово, цифра, символ, иероглиф, знак препинания и т.д.

Знаковые системы широко используются во многих областях, включая математику. В математике знаковые системы используются для передачи числовой информации, такой как десятичная, двоичная, восьмеричная и шестнадцатеричная системы.

Одна из ключевых концепций знаковых систем — это кодирование. Кодирование — это процесс, при котором информация преобразуется в знаки, которые могут быть переданы или сохранены для будущего использования.

Кодирование также является частью процесса декодирования. Декодирование — это преобразование знаков обратно в исходную информацию. Например, если число 123 закодировано в двоичную систему счисления как 1111011, то процесс декодирования позволит восстановить исходное число 123.

Другая важная концепция знаковых систем — это алфавит. Алфавит — это набор знаков, которые используются для кодирования информации. В математике алфавит может быть любым набором цифр, букв, знаков математических операций и т.д.

В целом, знаковые системы играют важную роль в передаче и хранении информации. В математике они используются для представления чисел и математических операций, что позволяет усложнять и совершенствовать вычисления.

Основные концепции

Одной из основных концепций знаковых форм для представления математической информации является ясность и наглядность выражения. Кроме того, знаковые формы должны быть универсальными, то есть понятными независимо от культурных различий и уровня образования.

Еще одной важной концепцией является эффективность используемых знаков и символов. Они должны быть простыми и легко запоминающимися, чтобы ускорить время обучения и улучшить результирующую коммуникацию.

Другими важными концепциями знаковых форм в математике являются их унификация и стандартизация. Только в таком случае мы можем быть уверены, что разные люди и организации используют одинаковые знаки и символы, что ускоряет и облегчает их взаимодействие.

Важно также учитывать, что знаки и символы должны быть гибкими и адаптивными к различным ситуациям. Например, они должны уметь сочетаться друг с другом и быть расширяемыми, чтобы позволить создавать новые знаки в соответствии с новыми математическими концепциями.

Наконец, важно учитывать, что знаковые формы должны быть легко освоимыми для детей и людей с ограниченными возможностями, что позволит им успешно изучать математику и является важным элементом социальной справедливости.

Классификация форм

Формы для представления математической информации могут быть классифицированы по различным критериям. Один из наиболее распространенных подходов — это классификация форм по типу содержащихся в них объектов. Согласно этому подходу, формы можно разделить на следующие типы:

• Графические формы — формы, содержащие графические объекты, такие как линии, кривые, фигуры и т.д. Такие формы часто используются в геометрии и визуализации математических понятий.
• Табличные формы — формы, содержащие таблицы с числовыми и текстовыми данными. Такие формы часто используются для представления статистических данных и результатов расчетов.
• Символьные формы — формы, содержащие символьные выражения, формулы и уравнения. Такие формы являются основным инструментом для работы с математическими понятиями в аналитической геометрии, математическом анализе и теории вероятностей.
• Динамические формы — формы, содержащие интерактивные элементы, такие как кнопки, поля для ввода данных и т.д. Такие формы позволяют пользователям взаимодействовать с математическими объектами и выполнять различные вычисления.

Каждый из типов форм имеет свои преимущества и недостатки, и выбор подходящей формы зависит от конкретной задачи и целей пользователя.

Примеры знаковых форм

1. Геометрические фигуры

Простые геометрические фигуры, такие как треугольники, квадраты, круги и прямоугольники, могут использоваться для представления информации в математике. Например, круг может быть использован для представления диаграммы Венна, которая показывает пересечение и разницу между множествами.

2. Цифры и знаки математических операций

Стандартные знаки математических операций, такие как плюс, минус, умножение и деление, также являются знаковыми формами. Они используются для быстрого и точного представления математических выражений и расчетов.

3. Графики и диаграммы

Графики и диаграммы могут представлять математическую информацию в визуальной форме. Например, график может показать зависимость между двумя переменными или изменение функции со временем. Диаграммы могут использоваться для показа статистических данных в удобной форме, такой как столбчатые и круговые диаграммы.

4. Формулы и уравнения

Формулы и уравнения представляют математические выражения в символической форме. Они могут использоваться для описания зависимостей между переменными, расчетов и решения математических проблем. Формулы и уравнения могут быть записаны в математическом языке или в виде текста с использованием знаков математических операций и символов.

5. Таблицы

Таблицы могут представлять числовую информацию в удобной форме. Они могут использоваться для записи результатов экспериментов, статистических данных или формул. Таблицы могут также использоваться для организации информации в электронных таблицах, таких как Microsoft Excel или Google Sheets.

Пример таблицы с числовыми даннымиСтранаНаселениеПлощадь, кв км

Россия	144 млн.	17,1 млн.
США	328 млн.	9,8 млн.
Канада	37 млн.	9,9 млн.

Плюсы и минусы

Плюсы:

1. Математические знаки и формулы позволяют описывать и анализировать разнообразные явления и процессы в природе, технике, экономике и других областях.
2. Использование знаков и формул упрощает и ускоряет вычисления, сокращает объем работы и повышает точность результатов.
3. Математические символы являются международным языком, что позволяет удобно и эффективно общаться между учеными и специалистами из разных стран.
4. Правильное использование знаков и формул способствует развитию логического мышления, улучшению абстрактного мышления и повышению уровня математической культуры.

Минусы:

• Некоторые математические понятия и символы сложны для понимания и могут вызвать затруднения у начинающих учащихся и людей, не имеющих математического образования.
• Нередко возникают разногласия и неоднозначности в трактовке символов и формул, что может привести к ошибкам и неправильным выводам.
• Иногда используемые знаки и формулы имеют ограниченную область применения и не могут полностью описывать сложные процессы и явления в реальном мире.

Итог: В целом, использование математических знаков и формул имеет больше плюсов, чем минусов, и является важным инструментом для научных исследований и прикладной деятельности.

Знаковые формы в образовании

Знаковые формы широко используются в обучении математике. Они помогают ученикам быстрее и эффективнее усваивать материал, представляя информацию более наглядно.

Одной из наиболее распространенных знаковых форм являются математические формулы. Они позволяют кратко и точно выразить сложные математические концепции, экономя время на записи и изучении. Кроме того, формулы удобно использовать в математических задачах, позволяя оперировать с числами и переменными более оперативно.

Другой популярной знаковой формой является графика. Графики помогают иллюстрировать функции и зависимости между переменными, делая математические концепции доступнее и более понятными ученикам.

Таблицы и диаграммы также являются знаковыми формами, которые используются в образовании для визуализации информации и облегчения процесса запоминания. Они могут содержать большое количество данных, которые легче воспринимать в упорядоченном и структурированном виде.

В целом, знаковые формы играют важную роль в обучении математике, помогая студентам лучше понимать математические концепции и оперировать информацией более эффективно.

Использование в других областях

Математические формулы и символы нашли применение не только в математике, но и в других научных областях. Например, в физике и химии они используются для обозначения законов, констант, формул. А в биологии, геологии и географии — для описания процессов, связанных с геометрией и статистикой.

Информационные технологии тоже включают математические символы и выражения. Они используются для программирования, описания алгоритмов и создания баз данных. Кроме того, эти символы облегчают обмен информацией и позволяют точнее выражать мысли.

Математические символы также нашли применение в дизайне и искусстве. Например, в графическом дизайне и архитектуре они используются для создания логотипов, шрифтов и других элементов. А в искусстве математические символы помогают создавать гипнотические рисунки, оптические иллюзии и другие эффекты.

• Итак, математические символы являются неотъемлемой частью многих научных областей
• Использование математических символов облегчает работу с данными и точнее выражает мысли
• Эти символы также находят применение в дизайне, искусстве и других областях

Вопрос-ответ:

Какие основные преимущества имеют знаковые формы для представления математической информации?

Основными преимуществами знаковых форм являются компактность и ясность представления математической информации. Они позволяют избежать излишней длинности и непонятности записи математических формул и выражений, а также могут использоваться для их упрощения и сокращения. Кроме того, знаковые формы могут быть удобны для визуализации геометрических фигур и динамических процессов.

Какие типы знаковых форм используются для представления математической информации?

Существует несколько типов знаковых форм, которые могут быть использованы для представления математической информации. К ним относятся графики, диаграммы, таблицы, матрицы, символы и др. Каждый тип знаковых форм имеет свои особенности и может быть удобен для представления определенных типов информации. Например, для представления функций чаще всего используются графики и диаграммы, а для матриц и линейных уравнений — символы и таблицы.

Какие основные концепции лежат в основе использования знаковых форм для представления математической информации?

Основными концепциями, лежащими в основе использования знаковых форм, являются абстракция, организация и визуализация. Абстракция позволяет выделять основные характеристики математических объектов и явлений, игнорируя всю лишнюю информацию. Организация представления математической информации позволяет упорядочить и структурировать ее, чтобы она была легко воспринимаема. Визуализация — это способ представления информации через знаковые формы, которые могут быть более понятны и доступны для восприятия.

Какие виды графиков могут быть использованы для представления математических функций?

Для представления математических функций могут быть использованы различные виды графиков. К ним относятся линейные графики, графики с полигонами частичных сумм, гистограммы, диаграммы рассеяния и др. Линейные графики являются наиболее распространенным типом графиков, они быстро и наглядно позволяют оценить изменение функции. Графики с полигонами частичных сумм используются для оценки сходимости рядов и последовательностей. Гистограммы позволяют оценить распределение случайных величин. Диаграммы рассеяния определяют зависимость между двумя наборами данных.

Какие типы таблиц и матриц могут быть использованы для представления математической информации?

Для представления математической информации могут быть использованы различные типы таблиц и матриц. К ним относятся прямоугольные и квадратные матрицы, треугольные матрицы, разреженные матрицы, таблицы со связями, таблицы с многомерными данными и др. Прямоугольные и квадратные матрицы используются для решения систем линейных уравнений и других математических задач. Треугольные матрицы бывают верхнетреугольными и нижнетреугольными и также используются для решения математических задач. Разреженные матрицы используются для представления данных, которые содержат множество нулевых элементов. Таблицы со связями используются для представления связанных данных. Таблицы с многомерными данными используются для представления данных, которые содержат несколько измерений.

Какие символы могут быть использованы для представления математических объектов и операций?

Символы могут быть использованы для представления различных математических объектов и операций. К ним относятся буквы алфавита и различные символы, такие как знаки операций, скобки, точки, запятые, индексы, верхние и нижние индексы и др. Буквы алфавита используются для обозначения переменных и констант. Знаки операций используются для обозначения математических операций, таких как сложение, вычитание, умножение и др. Скобки используются для обозначения группировки математических выражений. Индексы используются для обозначения позиции элемента в матрице или векторе.

Какие принципы следует учитывать при выборе знаковых форм для представления математической информации?

При выборе знаковых форм для представления математической информации следует учитывать несколько принципов. К ним относятся принцип удобочитаемости и понятности, принцип эффективности и компактности, принцип соответствия содержанию и принцип разнообразия. Принцип удобочитаемости и понятности заключается в том, что знаковые формы должны быть понятны и доступны для восприятия. Принцип эффективности и компактности заключается в том, что знаковые формы должны быть максимально экономичны по занимаемому месту и времени. Принцип соответствия содержанию заключается в том, что знаковые формы должны быть подходящими для представления конкретной математической информации. Принцип разнообразия заключается в том, что знаковые формы должны быть разнообразными, чтобы представлять математическую информацию в различных форматах.

Видео по теме: