Что такое звено в математике 4 класс
Содержимое
Звено в математике 4 класса — это элементарное понятие, которое помогает детям разобраться в основах арифметики. Узнайте, как понять и использовать звенья для решения уравнений и задач в 4 классе.
Звено — это понятие, которое широко используется в математике 4 класса. Оно помогает ученикам легче понять связь между разными математическими операциями и решить сложные задачи. В математике 4 класса звено является важным инструментом для развития логического мышления и аналитических навыков учеников.
Примеры звеньев в математике 4 класса:
- Звено равенства — это основное звено, которое помогает ученикам решить уравнения. Оно показывает, что два выражения равны между собой. Например, в уравнении «2 + 3 = 5» знак «равно» является звеном равенства.
- Звено неравенства — это звено, которое показывает, что одно выражение больше или меньше другого. Например, в неравенстве «7 > 5» знак «больше» является звеном неравенства.
- Звено последовательности — это звено, которое показывает, что числа следуют друг за другом по определенному порядку. Например, в последовательности «1, 2, 3, 4, 5» знак «запятая» является звеном последовательности.
Звено в математике 4 класса является важным инструментом для развития навыков решения задач и логического мышления учеников. Понимание понятия звена поможет им успешно справляться с различными математическими заданиями и развить интерес к предмету.
Что такое звено в математике

В математическом контексте звено может быть представлено в виде операции, выражения или действия, которое необходимо выполнить для решения задачи или получения ответа. Например, в простой арифметической задаче сложения чисел 2 и 3, каждое число является звеном, а сложение этих чисел является основным звеном.
Основное звено может состоять из нескольких элементарных звеньев, которые необходимо выполнить последовательно. Например, для решения задачи на нахождение площади прямоугольника с длиной сторон 4 и шириной 5 необходимо выполнить два элементарных звена: умножение чисел 4 и 5 и получение итогового результата.
Знание и понимание понятия звено в математике позволяет осуществлять последовательные операции и действия, а также разбивать сложные задачи на простые шаги. Это приносит ясность и структурированность в решении математических задач и способствует более эффективному и точному решению.
Зачем нужно изучать звено
Изучение звена также развивает логическое мышление учеников. Они учатся анализировать и устанавливать логические связи между числами и операциями. Это умение пригодится им не только в математике, но и в других предметах и в повседневной жизни.
Освоение понятия звена помогает ученикам улучшить свои навыки в решении математических задач. Они научатся применять звено для решения задач на сложение, вычитание, умножение и деление. Также они смогут использовать знание звена для решения задач на составление и расширение числовых выражений.
Изучение звена является важной частью математической программы в 4 классе. Понимая, как работает звено, ученики смогут успешно продолжить изучение математики на более высоких уровнях. Знание звена является фундаментом для изучения более сложных математических понятий и операций.
Как определить звено в задаче
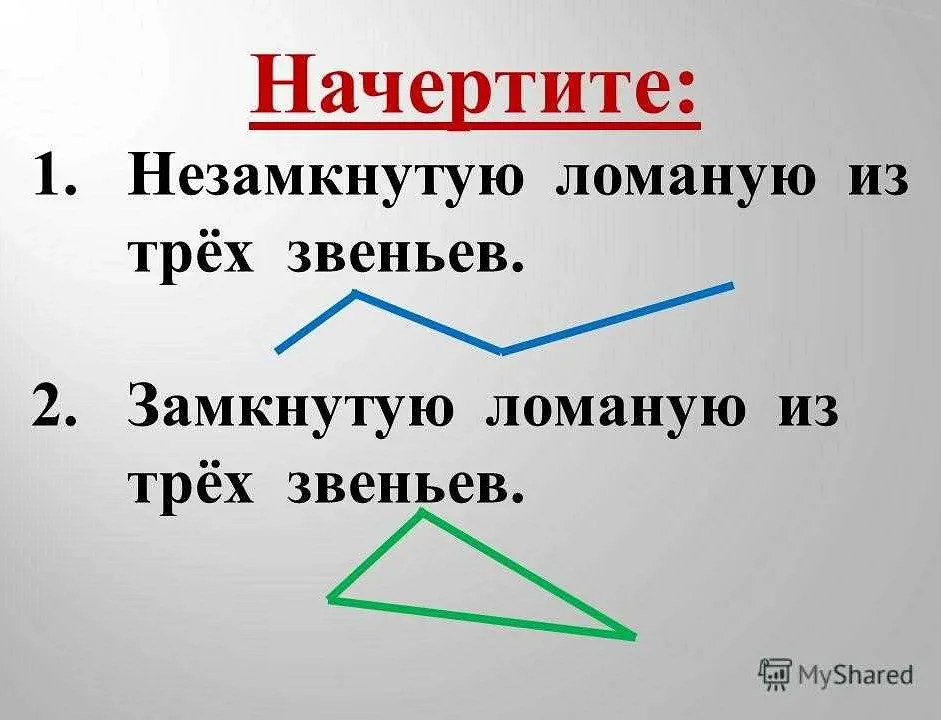
Определение звена в задаче может быть не всегда очевидным, поэтому следует внимательно прочитать условие задачи и выделить ключевые слова или операции, которые помогут определить звено. Например, если задача требует найти площадь прямоугольника, то звеном будет являться формула для вычисления площади, а также значения сторон прямоугольника.
Определение звена в задаче может быть разным в зависимости от типа задачи. В задачах на арифметические операции звеном может быть операция сложения, вычитания, умножения или деления. В задачах на пропорции звеном может быть соотношение между двумя величинами. В задачах на геометрию звеном может быть формула для вычисления площади, периметра или объема.
Важно помнить, что определение звена в задаче является ключевым шагом к ее успешному решению. После определения звена следует использовать правильную стратегию решения задачи, которая будет зависеть от типа и сложности задачи.
В заключение, определение звена в задаче является важным этапом решения математических задач. Прочитайте задачу внимательно, выделите ключевые слова и операции, определите звено, а затем примените соответствующую стратегию решения задачи. Такой подход позволит вам успешно справиться с задачами и развить свои математические навыки.
Примеры задач с звеном

1. В саду растут 12 яблонь. Каждая яблоня дает на 3 яблока больше, чем предыдущая. Сколько яблок дает последняя яблоня?
2. На столе лежит звено и две кнопки. Если нажать на первую кнопку, звено увеличится вдвое. Если нажать на вторую кнопку, звено уменьшится втрое. Сколько раз нужно нажать на каждую из кнопок, чтобы звено стало в 9 раз больше исходного?
3. В одной комнате стоят 4 стула, на каждом стуле сидит по 5 кукол. Сколько кукол всего сидит на стулах?
4. В спортзале есть 6 тренажеров. На каждом тренажере занимаются по 7 человек. Сколько человек занимается в спортзале?
5. В магазине продали 9 коробок с яблоками. В каждой коробке было по 4 яблока. Сколько яблок продали?
Звено в арифметике
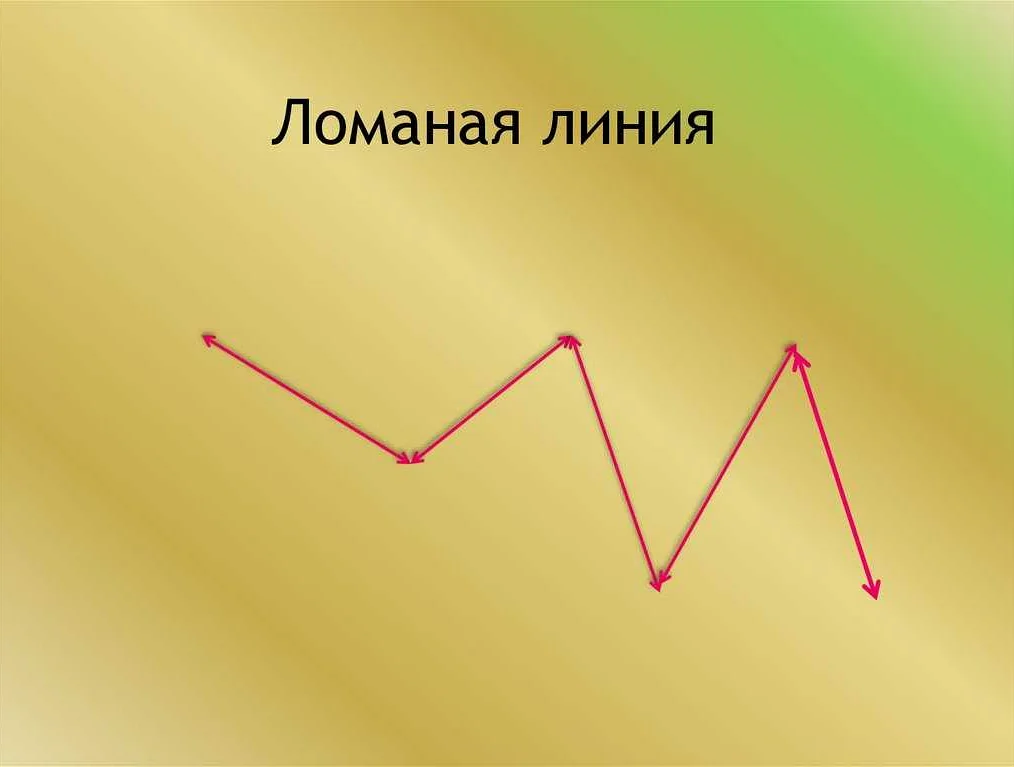
Примеры использования звена в арифметике:
- Сложение: если у нас есть два числа 5 и 3, звено сложения позволяет нам найти их сумму, которая составляет 8.
- Вычитание: если у нас есть число 7 и мы вычитаем из него число 4, звено вычитания позволяет нам найти разницу, которая равна 3.
- Умножение: если у нас есть число 2 и мы умножаем его на число 6, звено умножения позволяет нам найти произведение, которое равно 12.
- Деление: если у нас есть число 8 и мы делим его на число 2, звено деления позволяет нам найти частное, которое равно 4.
Таким образом, звено в арифметике является ключевым понятием, которое позволяет нам выполнять основные операции над числами и находить результаты этих операций.
Звено в геометрии
Звено может быть задано двумя точками, которые являются его конечными точками. Для обозначения звена используется буква «l» или «m» с верхним индексом, например «lAB» или «mCD».
Звено может быть прямым или кривым. Прямое звено — это отрезок прямой линии, которая соединяет две точки и не имеет изгибов. Кривое звено — это отрезок ломаной линии, которая соединяет две точки и имеет изгибы.
Для измерения длины звена используется единица измерения — метр или сантиметр. Длина звена можно измерить с помощью линейки или мерной ленты.
Примеры использования звена в геометрии:
Прямое звеноКривое звено
 |  |
Звено в алгебре
Например, в алгебре часто используются следующие звенья:
Сложение — это звено, которое позволяет складывать два числа или переменные. Например, 2 + 3 = 5.
Вычитание — это звено, которое позволяет вычитать одно число или переменную из другого. Например, 5 — 2 = 3.
Умножение — это звено, которое позволяет перемножать два числа или переменные. Например, 2 * 3 = 6.
Деление — это звено, которое позволяет делить одно число или переменную на другое. Например, 6 / 3 = 2.
Звенья в алгебре используются для составления и решения уравнений, нахождения неизвестных переменных, а также для проведения различных операций с числами. Понимание звеньев в алгебре является важным навыком для успешного изучения и применения алгебры.
Знание и понимание звеньев в алгебре помогает решать сложные задачи и строить математические модели, которые находят применение в различных областях науки и техники.
Видео по теме:
Что такое звено в математике?
Звено в математике — это число или символ, которое связывает другие числа или символы в математическом выражении. Оно может быть переменной, константой или операцией.
Какие примеры звеньев существуют в математике?
Примеры звеньев в математике включают числа (например, 5), переменные (например, x), операции (например, + или ×) и функции (например, sin(x)). Они могут быть частью математического выражения, уравнения или формулы.
Каким образом звенья используются в математических выражениях?
Звенья используются в математических выражениях для обозначения и связывания чисел и операций. Например, в выражении 2 + 3, звеньями являются числа 2 и 3, а операцией является сложение (+). Звенья также могут быть переменными, которые представляют неизвестные значения в уравнении.
Какова роль звеньев в математических выражениях?
Роль звеньев в математических выражениях состоит в том, чтобы представлять и связывать различные числа и операции. Они позволяют нам выражать математические идеи и решать уравнения. Без звеньев математические выражения были бы бессмысленными и неудобочитаемыми.
Что такое звено в математике?
Звено в математике — это одно из множества чисел, удовлетворяющих одному и тому же правилу.





Очень интересная и полезная статья! Я всегда задаюсь вопросом, зачем нам нужны звенья в математике, и, наконец, нашла ответ. Звено — это такая математическая операция, которая связывает два числа, чтобы получить третье. Вот так просто! Я теперь понимаю, что звено — это не только основа для дальнейших математических знаний, но и очень важный элемент в решении задач. Примеры из статьи помогли мне еще лучше понять, как работать с звенами. Теперь я смогу использовать их для составления уравнений и решения сложных задач. Большое спасибо за полезную информацию!