ABC в математике: что это такое и как применять в практике

A b c в математике — это обозначения для сторон треугольника, где ‘a’ — это длина стороны, противолежащей углу ‘A’, ‘b’ — длина стороны, противолежащей углу ‘B’, а ‘c’ — длина стороны, противолежащей углу ‘C’. Эта нотация помогает устанавливать соответствия между углами и их противоположными сторонами в треугольнике.

Математика является одним из основных предметов в школе и университете. И если в начальной школе учатся основам, то в старших классах и вузах изучают более сложные темы. Одной из таких тем является использование А, В, С в математике.

А, В, С — это просто буквы в алфавите, но в математике они имеют свой особый смысл и называются переменными. Они используются для представления различных значений в выражениях и уравнениях.

Знание А, В, С в математике очень важно, потому что благодаря этим переменным мы можем создавать выражения и уравнения для решения различных проблем в наших повседневных жизнях. Например, экономические модели или научные исследования часто используют эти переменные.

ABC в математике

ABC — это не только первые три буквы алфавита, но и аббревиатура, используемая в математике. В этой области науки ABC означает альфа-бетта-гамма, три переменные, которые обычно используются для обозначения углов или сторон в треугольниках или других геометрических фигурах. Каждый из этих символов может иметь различные значения в зависимости от контекста, в котором они используются.

Например, в геометрии угол A, B и C в треугольнике обозначают углы при вершинах A, B и C соответственно. Они могут использоваться для расчета площади треугольника или для нахождения других свойств треугольника.

ABC используется не только в геометрии, но и в других областях математики. Иногда эти символы могут использоваться в других комбинациях, как, например, AB или AC, что означает стороны треугольника.

Важно знать значение ABC и других обозначений в математике, чтобы правильно понимать математические выражения и формулы, а также использовать их в своих расчетах. Хотя это может показаться сложным в начале, с практикой вы начнете легче ориентироваться в символах и их значениях.

Видео по теме:

Что это и зачем нужно знать

Алфавитные формулы A, B, C или их аналоги являются важной частью учебной программы по математике. Это происходит по ряду причин, анализирующих различные аспекты математической науки.

Например, знание алфавитных формул может дать студентам лишь общее представление о различных аспектах математики, но это может быть достаточно, чтобы понять и осмыслить более сложные понятия. Кроме того, знание алфавитных формул позволяет определить паттерны в уравнениях и примерах, что повышает производительность в решении задач.

В математике алфавитные формулы используются для обозначения любого значимого значения, где буква может действовать как коэффициент, переменная, константа, функция или что-то другое. Таким образом, знание алфавитных формул помогает разобраться в сложных механизмах математической науки и дает более глубокое понимание темы.

Так что же это за алфавитные формулы? Примерами могут выступать A, B, C, X, Y и Z, которые можно заменить на любые другие буквы в соответствии с требуемыми математическими упражнениями. Знание таких формул и понимание их значения может дать глубокое понимание различных математических концепций и помочь увеличить успех в учебе в течение всей жизни.

Буквенные обозначения в математических формулах

Математика использует буквенные обозначения, чтобы обозначать конкретные объекты, без необходимости использования длинных описаний. В математических формулах, буквенные обозначения играют важную роль в объяснении и определении формул.

Например, буква «x» в уравнении «y = mx + b» обозначает неизвестное значение, которое нужно найти. Буквенные обозначения используются для обозначения других величин таких как скорость, ускорение, расстояние и т.д.

Кроме того, буквенные обозначения помогают сократить запись формулы, что делает ее более читабельной. Часто одна буква может быть использована для обозначения нескольких величин в разных уравнениях.

Но важно помнить, что буквенные обозначения в математике могут иметь различные значения в различных контекстах. Например, буква «x» может обозначать переменную в одном уравнении, а в другом уравнении она может обозначать координату на графике.

Поэтому важно внимательно читать формулы и анализировать буквенные обозначения, используемые в конкретном контексте, чтобы не возникло путаницы.

Алгебраические выражения с ABC

Алгебраическим выражением называется выражение, в котором могут содержаться числа, переменные и знаки математических операций. В частности, переменная может быть обозначена любой буквой, в том числе и буквами ABC.

Алгебраические выражения с ABC могут быть записаны в виде суммы или разности различных членов, где каждый член может содержать переменные A, B и C с указанием степени. Например, выражение 3A^2B — 5CB^2 + 2ABC является алгебраическим выражением с переменными A, B и C, где каждый член имеет свои коэффициенты и степени.

Алгебраические выражения с ABC используются в различных областях математики, физики, химии и техники для описания различных процессов и явлений. Например, выражения с ABC могут быть использованы для описания движения тела в пространстве, распространения электромагнитных волн или химических реакций.

Для упрощения и работы с алгебраическими выражениями с ABC используются различные методы и правила, такие как раскрытие скобок, сокращение подобных членов, факторизация и т.д. Знание этих методов и правил позволяет проще и быстрее решать задачи, связанные с алгебраическими выражениями в области науки и техники.

Геометрические фигуры с ABC

В математике буквы A, B, C часто используются для обозначения вершин геометрических фигур. Это могут быть треугольники, многоугольники, круги.

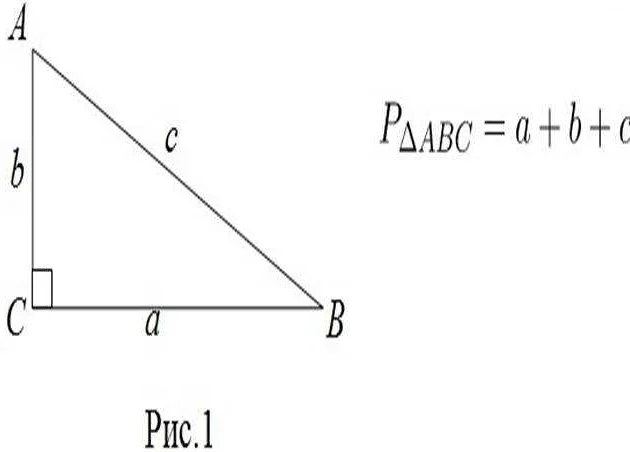
Один из самых известных треугольников — это прямоугольный треугольник ABC. Здесь A, B и C — названия вершин. Сторона AB называется катетом, сторона AC называется катетом или прилегающей катету гипотенузой, а сторона BC называется другой катетой. Формулой Пифагора можно найти длину любой стороны треугольника, если известны длины двух других сторон.

Треугольник ABC может быть также равнобедренным, когда две стороны равны между собой, или равносторонним, когда все стороны равны. Равносторонний треугольник ABC имеет три равных угла по 60 градусов, а его площадь можно вычислить по формуле: S = (a^2*sqrt(3))/4, где a — длина стороны.

Также буквы A, B, C могут использоваться для обозначения вершин многоугольника, например, четырехугольника ABCD или пятиугольника ABCDE. Здесь нужно знать свойства разных многоугольников, например, формулу для вычисления площади квадрата, равную S = a^2, где a — длина стороны.

В круге буква A может означать центр круга, а буква B — точку на окружности. Радиус круга обозначается буквой R, а длина окружности — буквой C. Площадь круга можно найти по формуле S = π*R^2, где π — число пи (приблизительно равно 3.14).

Таким образом, буквы A, B, C могут помочь в описании свойств различных геометрических фигур и помочь в решении математических задач.

ABC в тригонометрии

В тригонометрии A, B и C обозначают углы треугольника. Аngles B и C называются соответственно меньшим и большим углами, а угол А лежит напротив стороны с наибольшей длиной, которую мы обычно обозначаем буквой c. Отношение сторон треугольника связано с тригонометрическими функциями: синус (sin), косинус (cos) и тангенс (tan).

Как определить значения тригонометрических функций углов треугольника ABC? Используя соотношения:

• обозначим длины сторон треугольника A, B, C через a, b, c соответственно;
• затем, используя теорему Пифагора, определим квадраты длин оставшихся двух сторон: a² + b² и c²;
• наконец, применив тригонометрические отношения, мы найдем значения sin, cos и tan всех трех углов (градусов).

Зная значения тригонометрических функций углов треугольника ABC, мы можем решать задачи на нахождение длин сторон, углов и высот. Важно понимать, что в тригонометрии углы могут быть выражены в градусах или радианах, и в зависимости от этого могут меняться формулы для расчета тригонометрических функций.

Таблица значений тригонометрических функций углов ABC при разных значениях сторон a, b, cУголSinCosTan

А	sin(A) = a/c	cos(A) = b/c	tan(A) = a/b
B	sin(B) = b/c	cos(B) = a/c	tan(B) = b/a
C	sin(C) = a/b	cos(C) = c/b	tan(C) = a/c

ABC в физике и механике

В физике и механике ABC – это мнемоническое правило, которое помогает запомнить основные составляющие векторов: направление, величину и точку приложения.

А – направление (англ. angle). Вектор всегда имеет определенное направление, которое определяется углом между вектором и осью координат.

B – величина (англ. magnitude). Вектор характеризуется своей длиной, которая является величиной вектора.

C – точка приложения (англ. point of application). Каждый вектор начинается в определенной точке, от которой измеряется его направление и величина.

ABC-правило применяется в различных областях физики и механике, например, при изучении движения тел, при работе с силами или при определении векторного произведения. Знание данного правила позволяет лучше понимать происходящие процессы и корректно решать задачи.

Важно отметить, что ABC-правило позволяет вычислить результат складывания векторов только в плоскости. Для работы с трехмерными векторами используется дополнительное правило – правило правой руки.

Таким образом, знание ABC-правила является обязательным для успешного изучения физики и механики. Оно помогает лучше понимать основные понятия, а также решать задачи и производить сложения векторов в плоскости.

ABC в экономике и финансах

ABC-анализ является одним из наиболее эффективных методов контроля за запасами в компании. Это позволяет уменьшить издержки на хранение, снизить зависимость от внешних поставщиков и ускорить процесс поставки продукции на рынок.

ABC-анализ работает по принципу деления товаров на три категории: A, B и C. Категория A фокусируется на топ-20% товаров, которые приносят наибольшую долю выручки для компании. Категория B включает товары, которые приносят от 20% до 30% выручки, а категория C – товары, которые приносят менее 10% выручки, но составляют большую часть общего количества.

При использовании системы ABC-анализа, компании могут сосредоточить свое внимание на группах товаров, которые приносят наибольшую выручку, и оптимизировать свой их уровень запасов. Это позволяет уменьшить общие затраты на транспортировку и хранение.

Кроме того, ABC-анализ является необходимым инструментом в управлении финансами и инвестициями. Применение метода ABC-анализа во финансовой аналитике позволяет упорядочить инвестиции по приоритетам, определить более эффективное использование ресурсов и повысить доходность портфеля инвестиций.

Таким образом, знание ABC-анализа в экономике и финансах является ключевым, чтобы принимать правильные решения в управлении производственными запасами и повышении доходности инвестиций.

Использование ABC в программировании

ABC (Abstract Base Class) – это механизм, позволяющий определять абстрактные классы в Python. Абстрактный класс – это класс, который содержит абстрактные методы, т.е. методы без реализации. Он может представлять собой набор правил, образцов для других классов.

ABC позволяет определить общий интерфейс для классов, которые не обязаны иметь общую реализацию. Это помогает организовать код и инкапсулировать логику, так как абстрактный класс может иметь только общие методы и свойства, которые в дальнейшем наследуются классами-потомками.

Пример использования ABC:

• Создание абстрактного класса:

from abc import ABC, abstractmethod

class Animal(ABC):

@abstractmethod

def make_sound(self):

pass

• Создание класса-потомка, который наследует абстрактный класс:

class Dog(Animal):

def make_sound(self):

return «Woof!»

В данном примере класс Animal является абстрактным классом, метод make_sound является абстрактным методом, который должен быть реализован в классе-потомке. Класс Dog наследует класс Animal и реализует метод make_sound.

Если создать объект класса Animal, то возникнет ошибка:

• Ошибочный код:

animal = Animal()

Ошибка:

TypeError: Can’t instantiate abstract class Animal with abstract methods make_sound

Эта ошибка связана с тем, что нельзя создавать объект абстрактного класса, который содержит абстрактные методы. Применение ABC позволяет избежать ошибок при работе с классами, а также упрощает написание и поддержку кода.

ABC в логике и математической философии

ABC — это не только буквы в математике, но также обозначение трех основных понятий в логике и математической философии — абстракции, бинарности и континуума. Эти понятия играют важную роль в понимании основ математики и ее приложений, а также в понимании самих основ математической логики.

Абстракции определяются как обобщенные представления о единичных объектах, которые используются для создания концептуальных моделей. Это понятие также включает идею о представлении объектов и их свойств в абстрактной форме, например, в виде символов или формул.

Бинарность в математике описывает арифметические операции, такие как сложение и умножение, которые осуществляются над парами чисел. В логике бинарность означает возможность деления на две категории или класса объектов, что может быть ценным инструментом для анализа и организации больших объемов данных.

Континуум — это понятие, которое описывает бесконечность и непрерывность. Оно основано на идее о бесконечно малых величинах, которые используются в математических и физических расчетах. В логике континуум часто относится к идеям о неопределенности, пределах и возможностях приближения, в том числе в контексте теории множеств.

Таким образом, понимание ABC в логике и математической философии может помочь улучшить понимание фундаментальных понятий в математике и логике, а также обеспечить критический взгляд на сложные и абстрактные концепты.

ABC в играх и головоломках

ABC — это не только первые три буквы английского алфавита, но и один из способов описания игровых элементов и головоломок, которые требуют логического мышления и сообразительности.

Примером такой головоломки может служить игра «Судоку», где нужно заполнить таблицу числами таким образом, чтобы в каждой горизонтали, вертикали и блоке 3х3 были все цифры от 1 до 9. Однако, кроме самой игры, есть еще и варианты, где вместо цифр используется набор букв ABC. Такие головоломки известны как ABC-судоку.

Еще один пример — логические задачи, где нужно расставить фишки или блоки таким образом, чтобы они закрыли все доступные площадки на игровом поле. Обычно эти задачи имеют несколько уровней сложности, причем для самых сложных требуется не только хорошее логическое мышление, но и скорость принятия решений.

Также ABC-головоломки могут включать в себя уровни, где нужно продолжить последовательность букв, угадать их место в ряду, найти закономерность, следуя которой можно решать задачи. Очень часто подобные игры используются для тренировки логики и тренировки мышления.

Короче говоря, ABC-элементы широко используются в играх и головоломках, требующих логики и сообразительности. Они могут быть легкими задачами для начинающих или крайне сложными, потребовавшими от игроков многократной попытки и терпения. Однако, несмотря на разный уровень сложности, каждая ABC-головоломка представляет собой увлекательный вызов для игрока.

Примеры использования ABC в реальной жизни

Английский алфавит — это система букв, символов и знаков препинания, которые используются для написания и чтения в английском языке. Он состоит из 26 букв, которые обозначаются с помощью ABC. Изучение алфавита важно для обучения языку и для коммуникации в письменной форме.

В школьной математике A, B и C представляют собой коэффициенты в уравнениях. Например, если есть уравнение 3x + 4y = 5, то 3 обозначает A, 4 обозначает B, а 5 обозначает C. Это уравнение можно использовать для решения различных проблем, таких как вычисление процентов, расходов и доходов.

В бизнесе ABC-анализ используется для управления запасами и прибыльностью. Этот метод группирует товары в три категории: A, B и С. Категория A представляет собой товары с наибольшей прибыльностью и наименее расходами, B – товары со средними характеристиками, а C – товары с наименьшей прибыльностью и наибольшими расходами. Этот анализ помогает организациям принимать решения о том, какие товары следует продавать, а какие оставлять на складе.

В математическом анализе А, В и С используются для обозначения точек на плоскости или в пространстве. Координаты точки A могут быть обозначены как (x1, y1), координаты точки B – (x2, y2) и координаты точки С – (x3, y3). Это позволяет производить операции с точками, как например, вычисление расстояния между точками, нахождение углов между векторами, нахождение точек пересечения и т.д.

ABC-технология – это метод инвентаризации и управления запасами, который используются в производственной сфере. Он состоит в разделении запасов на три категории: A, B и C. Запасы категории A – это товары с высоким уровнем спроса, B – средним уровнем спроса, а C – с низким уровнем спроса. Такая классификация помогает организовать процесс производства и отслеживать общее состояние запасов.

Вопрос-ответ:

Что такое ABC-анализ в математике и для чего он нужен?

ABC-анализ — это метод, используемый для управления инвентарными запасами или распределения важности задач. В математике ABC-анализ используется для классификации элементов тройкой: А (наиболее важные элементы), В (средней важности) и С (наименее важные). Необходимо знать этот метод, чтобы определить, какие элементы являются критическими в ваших задачах или операциях.

Можно ли применять ABC-анализ в финансовой сфере, чтобы управлять бюджетом?

Да, ABC-анализ может быть использован в финансах для управления бюджетом. Например, если вы используете этот метод для классификации расходов, то можете выяснить, какие из них являются наиболее значимыми и на что нужно сосредоточиться в первую очередь. Таким образом, можно управлять бюджетом более эффективно.

Как использовать ABC-анализ в логистике?

ABC-анализ широко используется в управлении запасами и логистике. Метод позволяет управлять запасами, учитывая потребительский спрос и логистические затраты. А-элементы (наиболее важные) могут храниться ближе к месту производства или распределения, чтобы сократить затраты на транспортировку. B-элементы можно хранить в промежуточных складах, а C-элементы — в удаленных складах или заказывать их по мере необходимости.

Что такое абакус и для чего он используется?

Абакус — это старинный счетный прибор, позволяющий производить арифметические операции (сложение, вычитание, умножение, деление) с помощью перемещения шариков по прутьям. Абакус используется для решения математических задач, особенно в торговле и финансовой сфере. Существуют различные типы абакусов, используемые в разных культурах и временных периодах.

Какие математические функции применяются в экономике?

В экономике часто применяются различные математические функции для моделирования экономических процессов. Некоторые из них включают линейную, квадратичную, логарифмическую, экспоненциальную, синусоидальную и логистическую функции. С помощью этих функций экономисты могут анализировать данные, прогнозировать будущие тенденции и принимать управленческие решения.

Что такое комплексные числа и для чего они нужны?

Комплексные числа — это числа, которые состоят из двух компонент: действительной и мнимой части (i). Они используются в математике, физике, инженерии и других науках для описания систем, которые не могут быть описаны действительными числами, например, электрических цепей, колебательных процессов и т.д. Кроме того, комплексные числа используются в теории вероятностей и статистике.

Какие математические методы используются в искусственном интеллекте?

Искусственный интеллект использует множество математических методов, включая линейную алгебру, статистику, оптимизацию, теорию графов, машинное обучение, нейронные сети и многое другое. Эти методы используются для разработки алгоритмов, которые могут обрабатывать и анализировать данные, распознавать образы, генерировать речь и т.д. Кроме того, математические методы помогают оптимизировать обработку данных и улучшать эффективность работы алгоритмов.