Площадь треугольника как найти 4 класс математика
Содержимое
- 1 Площадь треугольника как найти 4 класс математика
- 1.1 Что такое площадь треугольника?
- 1.2 Формула для расчета площади треугольника
- 1.3 Как найти основание треугольника?
- 1.4 Как найти высоту треугольника?
- 1.5 Как найти боковую сторону треугольника?
- 1.6 Примеры вычисления площади треугольника
- 1.7 Как проверить правильность вычислений?
- 1.8 Вопрос-ответ:
- 1.8.0.1 Как найти площадь треугольника в 4 классе?
- 1.8.0.2 Как найти площадь треугольника, если известны длины всех его сторон?
- 1.8.0.3 Как найти площадь треугольника, если известны координаты его вершин?
- 1.8.0.4 Как найти площадь треугольника, если известны его высота и основание?
- 1.8.0.5 Как найти площадь треугольника, если известны координаты его вершин?
- 1.9 Видео по теме:
Узнайте, как найти площадь треугольника в 4 классе математики. Полезные советы и простые формулы для решения этой задачи.
Вычисление площади треугольника является одной из основных задач в изучении геометрии. Даже в 4 классе математики ученики уже могут научиться находить площадь треугольника, используя простые методы.
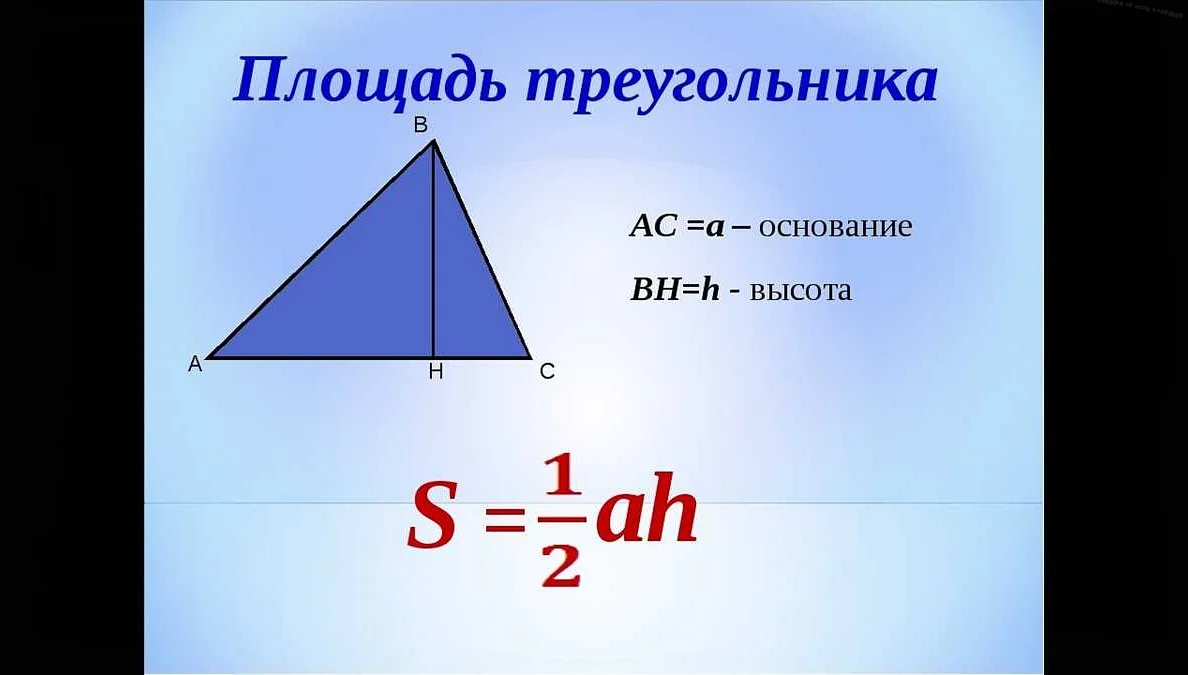
Первый шаг в нахождении площади треугольника — определить его основание и высоту. Основание треугольника это одна из его сторон, а высота — отрезок, проведенный из вершины треугольника и перпендикулярный основанию.
Для вычисления площади треугольника в 4 классе используется формула: площадь = (основание * высота) / 2. Основание и высоту треугольника можно измерить в сантиметрах или в любых других единицах длины.
Например, если основание треугольника равно 6 см, а высота равна 4 см, то площадь треугольника будет равна (6 * 4) / 2 = 12 см².
Таким образом, нахождение площади треугольника в 4 классе математики не является сложной задачей, если ученик знает, как найти основание и высоту треугольника и применить формулу для вычисления площади.
Что такое площадь треугольника?
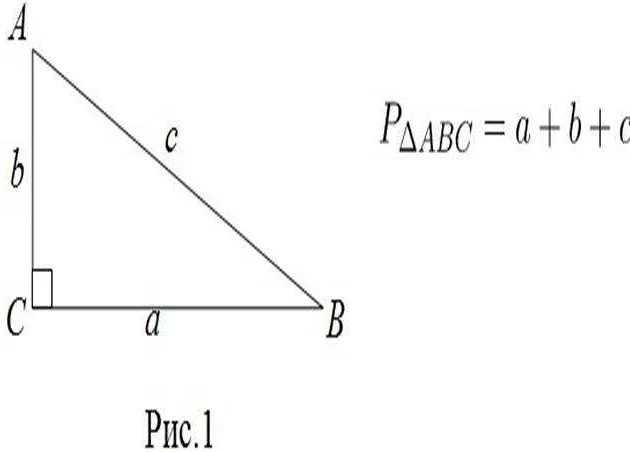
Площадь треугольника можно найти, зная длины его сторон или зная длины основания и высоты. Существует несколько формул, которые помогают нам вычислить площадь треугольника в разных случаях.
Например, если мы знаем длины основания и высоты треугольника, мы можем использовать формулу:
| Площадь треугольника | = | 1/2 x длина основания x высота |
Если же мы знаем длины всех трех сторон треугольника, мы можем использовать формулу Герона:
| Площадь треугольника | = | √(p x (p — a) x (p — b) x (p — c)) |
где a, b и c — длины сторон треугольника, а p — полупериметр треугольника (сумма длин всех сторон, деленная на 2).
Зная эти формулы, мы можем легко найти площадь треугольника и использовать эту информацию для решения различных задач.
Формула для расчета площади треугольника

Для расчета площади треугольника используется специальная формула, которая основывается на длине основания треугольника и его высоте. Формула для нахождения площади треугольника выглядит следующим образом:
| Площадь треугольника (S) = | 1/2 | × | Длина основания (b) | × | Высота треугольника (h) |
В этой формуле, длина основания треугольника (b) — это одна из его сторон, а высота треугольника (h) — это перпендикуляр, опущенный из вершины треугольника на основание. Обрати внимание, что высота должна быть измерена от основания до вершины, а не до противоположной стороны.
Давай рассмотрим пример. Предположим у нас есть треугольник со стороной основания равной 10 см и высотой, опущенной на это основание, равной 6 см. Чтобы найти площадь этого треугольника, мы можем использовать формулу:
| S = | 1/2 | × | 10 см | × | 6 см |
Расчитаем:
| S = | 1/2 | × | 10 см | × | 6 см |
| S = | 1/2 | × | 60 см² | ||
| S = | 30 см² |
Таким образом, площадь этого треугольника равна 30 квадратным сантиметрам.
Формула для расчета площади треугольника очень полезна и может быть использована для решения различных задач, связанных с треугольниками. Она поможет нам определить площадь треугольника, даже если у нас нет возможности измерить все его стороны.
Как найти основание треугольника?

Если треугольник задан своими сторонами, то основание можно найти, определив самую длинную из них. Эта сторона и будет основанием треугольника.
Если треугольник задан своими вершинами в координатной плоскости, то основание можно найти, определив самую длинную горизонтальную сторону треугольника. Горизонтальная сторона треугольника – это сторона, у которой координаты вершин имеют одинаковые значения по оси OX.
Основание треугольника играет важную роль при вычислении его площади. Для решения задачи о площади треугольника необходимо знать длину основания и высоту треугольника, которая проведена к основанию. Поэтому понимание, как найти основание треугольника, является важным шагом в изучении этой темы.
Как найти высоту треугольника?
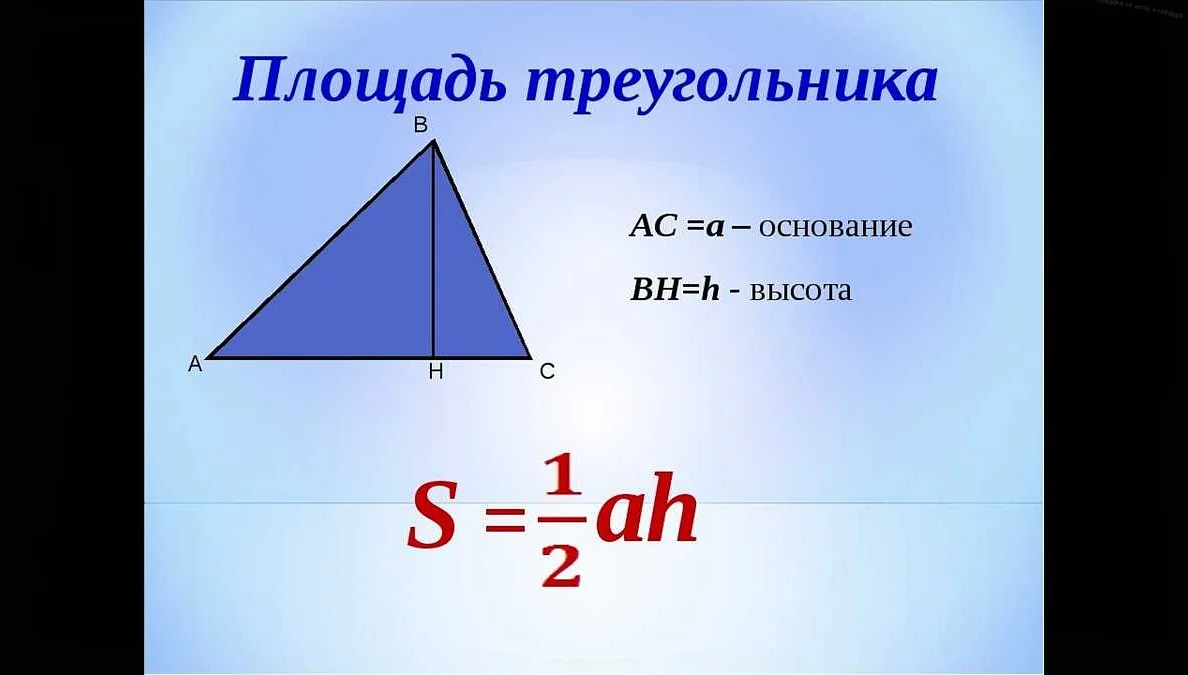
1. Используя формулу для высоты треугольника:
Высота треугольника может быть найдена с использованием формулы:
h = (2 * S) / a,
где h — высота, S — площадь треугольника, a — длина основания треугольника.
2. Используя свойства прямоугольного треугольника:
Если треугольник является прямоугольным, то высота будет являться длиной стороны, проведенной к противоположному углу от прямого угла.
3. Используя свойства равнобедренного треугольника:
Если треугольник является равнобедренным, то высота будет являться высотой, проведенной из вершины треугольника к основанию, перпендикулярной основанию и одновременно являющейся медианой.
4. Используя методы измерения:
Высоту треугольника можно также найти, используя линейку или другие инструменты измерения. Отметьте вершину треугольника и проведите прямую линию до противоположной стороны.
Зная основание треугольника и площадь, можно вычислить высоту треугольника с помощью формулы. Если треугольник прямоугольный или равнобедренный, высота может быть найдена с использованием соответствующих свойств треугольников. Если необходимо, можно также использовать методы измерения для нахождения высоты.
Как найти боковую сторону треугольника?

Для нахождения боковой стороны треугольника, необходимо знать длину его других сторон и углы между ними. В зависимости от известных данных, можно использовать различные методы:
- Метод синусов: Если известны длины двух сторон треугольника и угол между ними, можно воспользоваться следующей формулой: a = (b * sin(C)) / sin(A), где a — искомая боковая сторона, b — известная сторона, C — известный угол, A — угол, противолежащий известной стороне.
- Теорема косинусов: Если известны длины всех трех сторон треугольника, можно воспользоваться формулой: a = sqrt(b^2 + c^2 — 2 * b * c * cos(A)), где a — искомая боковая сторона, b и c — известные стороны, A — угол, противолежащий искомой стороне.
- Теорема Пифагора: Если треугольник является прямоугольным и известны длины двух его сторон, можно воспользоваться формулой: a = sqrt(b^2 + c^2), где a — искомая боковая сторона, b и c — известные стороны.
Важно помнить, что для применения этих методов нужно знать не менее чем одну известную сторону и угол треугольника.
Примеры вычисления площади треугольника
Давайте рассмотрим несколько примеров вычисления площади треугольника.
Пример 1:
У нас есть треугольник с основанием 5 см и высотой 3 см. Чтобы найти площадь треугольника, мы можем использовать формулу: Площадь = (Основание × Высота) ÷ 2.
Подставляем значения: Площадь = (5 см × 3 см) ÷ 2 = 15 см² ÷ 2 = 7.5 см².
Пример 2:
Предположим, что у нас есть треугольник, у которого длины сторон равны 4 см, 7 см и 9 см. Мы можем использовать формулу Герона для вычисления площади треугольника в этом случае: Площадь = √(p × (p — a) × (p — b) × (p — c)), где p — полупериметр треугольника, равный сумме длин всех сторон, деленной на 2.
Вычисляем полупериметр: p = (4 см + 7 см + 9 см) ÷ 2 = 20 см ÷ 2 = 10 см.
Подставляем значения в формулу: Площадь = √(10 см × (10 см — 4 см) × (10 см — 7 см) × (10 см — 9 см)) = √(10 см × 6 см × 3 см × 1 см) = √(180 см²) ≈ 13.42 см².
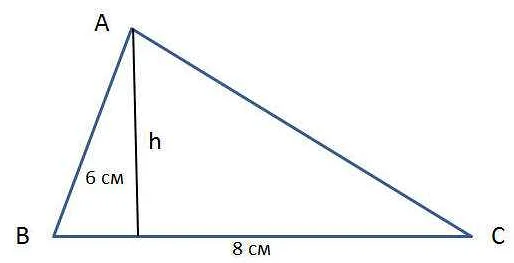
Пример 3:
Пусть у нас есть треугольник с основанием 10 см и высотой 8 см. Мы можем использовать формулу: Площадь = (Основание × Высота) ÷ 2.
Подставляем значения: Площадь = (10 см × 8 см) ÷ 2 = 80 см² ÷ 2 = 40 см².
Теперь вы знаете, как вычислять площадь треугольника на примере разных ситуаций. Помните, что площадь треугольника зависит от длины его основания и высоты или от длин всех его сторон.
Как проверить правильность вычислений?
После того, как мы вычислили площадь треугольника, мы можем проверить правильность наших вычислений. Вот несколько способов проверить правильность:
1. Проверка по формуле: Мы можем проверить, что наши вычисления соответствуют формуле для площади треугольника. Формула для площади треугольника: площадь = (основание * высота) / 2. Если мы правильно подставили значения основания и высоты в эту формулу, то полученное значение должно быть равно нашим вычислениям.
2. Проверка по геометрическим свойствам: Мы можем также проверить правильность наших вычислений, используя геометрические свойства треугольника. Например, если мы знаем, что площадь треугольника не может быть отрицательной или нулевой, то это может служить индикатором неправильного вычисления.
3. Проверка по результатам других методов: Если у нас есть возможность использовать другие методы для вычисления площади треугольника (например, разделение треугольника на два прямоугольных треугольника), мы можем проверить, совпадают ли результаты с нашими исходными вычислениями. Если результаты различаются, это может указывать на ошибку в вычислениях.
Важно помнить, что проверка правильности вычислений является важной частью математической работы. Проводя проверку, мы можем быть уверены в том, что наши результаты верны и достоверны.
Вопрос-ответ:
Как найти площадь треугольника в 4 классе?
В 4 классе можно найти площадь треугольника, зная его высоту и основание. Формула для расчета площади треугольника выглядит так: S = (h * a) / 2, где S — площадь треугольника, h — высота, a — основание.
Как найти площадь треугольника, если известны длины всех его сторон?
Если известны длины всех сторон треугольника, можно воспользоваться формулой Герона для расчета площади. Формула выглядит так: S = sqrt(p * (p — a) * (p — b) * (p — c)), где S — площадь треугольника, p — полупериметр треугольника, a, b, c — длины сторон треугольника.
Как найти площадь треугольника, если известны координаты его вершин?
Если известны координаты вершин треугольника, можно воспользоваться формулой для расчета площади по координатам. Формула выглядит так: S = 0.5 * |(x1 * (y2 — y3) + x2 * (y3 — y1) + x3 * (y1 — y2))|, где S — площадь треугольника, (x1, y1), (x2, y2), (x3, y3) — координаты вершин треугольника.
Как найти площадь треугольника, если известны его высота и основание?
Если известны высота и основание треугольника, можно воспользоваться формулой для расчета площади по высоте и основанию. Формула выглядит так: S = (h * a) / 2, где S — площадь треугольника, h — высота, a — основание.
Как найти площадь треугольника, если известны координаты его вершин?
Если известны координаты вершин треугольника, можно воспользоваться формулой для расчета площади по координатам. Формула выглядит так: S = 0.5 * |(x1 * (y2 — y3) + x2 * (y3 — y1) + x3 * (y1 — y2))|, где S — площадь треугольника, (x1, y1), (x2, y2), (x3, y3) — координаты вершин треугольника.


Статья на тему «Как найти площадь треугольника в 4 классе математики: подробное объяснение» оказалась очень полезной и понятной. Я всегда хотел понять, как рассчитывать площадь треугольника, но раньше это казалось мне сложным. Благодаря этой статье, я узнал, что есть несколько способов найти площадь треугольника, и все они очень простые. Автор начал с объяснения, что такое площадь и почему она важна. Затем он пошагово объяснил каждый способ нахождения площади треугольника. Например, один из способов — это умножить длину основания треугольника на его высоту и разделить полученное значение на 2. Я был приятно удивлен, как это просто и понятно объяснено. Также автор представил некоторые примеры и задачи, чтобы показать, как применять эти формулы на практике. Это очень помогло мне улучшить свои навыки решения задач. Я даже попробовал решить несколько задач самостоятельно и смог справиться с ними благодаря четкому объяснению в статье. Кроме того, автор предложил несколько дополнительных математических игр и задач, чтобы продолжить тренировку и развитие навыков решения задач. Я обязательно попробую их в ближайшее время. В целом, я доволен этой статьей. Она помогла мне понять, как найти площадь треугольника, и дала мне возможность применить полученные знания на практике. Спасибо автору за такое подробное и понятное объяснение!
Замечательная статья! Мне очень понравилось, как подробно и понятно объяснено, как найти площадь треугольника в 4 классе математики. Я всегда считал, что это сложная задача, но благодаря вашим пошаговым инструкциям я теперь понимаю, что это на самом деле не так уж и сложно. Особенно мне понравилось объяснение с использованием формулы «половина основания умножить на высоту». Такой метод подходит даже для самых маленьких школьников и помогает легко и быстро решить задачу. Теперь я с уверенностью могу помочь своему ребенку с домашними заданиями по математике. Спасибо за такое понятное объяснение и полезную информацию! Жду еще больше подобных статей.
Статья очень полезная и понятная. Я рада, что автор подробно объяснил, как найти площадь треугольника в 4 классе. Я всегда думала, что это сложно, но оказывается, все не так страшно. Теперь я поняла, что нужно умножить длину основания на высоту и разделить полученное значение пополам. Это легко запомнить, и я смогу применить эту формулу в следующий раз, когда буду решать задачи по математике. Большое спасибо автору за понятное объяснение!