Частное и разность в математике: понимание и применение основных понятий

Частное и разность — основные понятия математики, используемые в различных математических операциях. Частное — это результат деления двух чисел, а разность — разница между двумя числами. Узнайте больше о том, как эти понятия используются в математике и как совершать операции с ними.

Частное и разность являются одними из основных математических понятий. Они используются в различных областях математики, физики, экономики и других наук. Например, они помогают решать задачи на сравнение текущих и прошлых значений, вычисление процентной разницы, определение прироста или убыли.

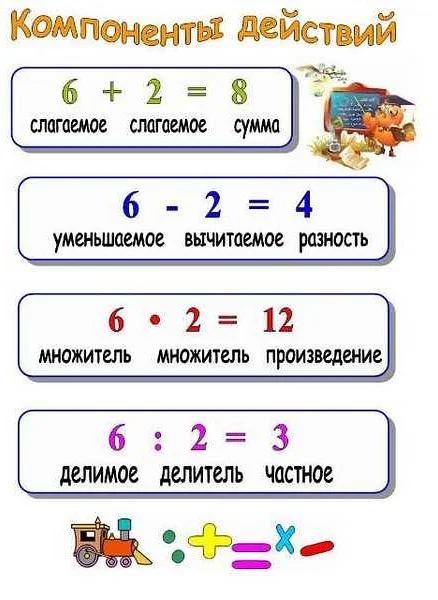
Частное обычно обозначается как результат деления одного числа на другое. Это показывает, сколько раз одно число входит в другое. Например, если имеется 9 яблок и 3 человека, которые хотят поделить их поровну, то каждый человек получит 3 яблока. Здесь 9 яблок являются делимым, 3 человека – делителем, а 3 яблока – частным.

Разность, в свою очередь, представляет собой результат вычитания одного числа из другого. Это показывает, насколько одно число отличается от другого. Например, если имеется 7 яблок и 3 человека, которые уже получили по 2 яблока, то осталось 1 яблоко. Здесь 7 яблок – уменьшаемое, 2 яблока – вычитаемое, 1 яблоко – разность.

Таким образом, частное и разность играют важную роль в математике и имеют практическое применение в повседневной жизни.

Для чего нужно знать частное и разность в математике

Частное и разность являются одними из основных операций в математике. Их знание необходимо для решения различных математических задач и ситуаций в повседневной жизни. Вот несколько примеров:

• Финансовые расчеты. В экономике и бизнесе необходимо уметь вычислять процентные ставки, расчеты по кредитам и другие финансовые операции. Частное и разность используются в таких задачах регулярно.
• Геометрия и физика. Реже, но также важно знать частное и разность в задачах, связанных с геометрией и физикой. Они понадобятся для вычисления длины или площади фигур, а также в процессе решения уравнений и законов физики.
• Повседневные задачи. В жизни неизбежно возникают разные ситуации, которые требуют знания частного и разности. Например, нужно распределить сладости между детьми поровну или вычислить разницу во времени между двумя городами.

Кроме того, знание частного и разности полезно для развития критического мышления и логического мышления. Они помогают людям анализировать и понимать информацию, решать задачи и принимать важные решения.

Таким образом, знание частного и разности в математике является важным навыком в повседневной жизни и помогает в решении различных задач и ситуаций.

Видео по теме:

Определение понятий «частное» и «разность»

Частное — это результат деления одного числа на другое. Например, если мы делим число 10 на число 2, то получаем частное равное 5.

Разность — это результат вычитания одного числа из другого. Например, если мы вычитаем число 7 из числа 15, то получаем разность равную 8.

Понятия частное и разность являются основными математическими операциями. Они используются в различных областях жизни, например, в экономике, физике, инженерии и др.

Частное и разность также используются для решения математических задач. Например, для вычисления скорости движения автомобиля используют формулу скорости, которая использует частное и разность.

В общем, понимание понятий частное и разность является важным в математике и на практике и поможет решать множество разнообразных задач.

Как правильно вычислять частное и разность

Частное и разность являются базовыми математическими понятиями, которые широко используются в различных областях науки и техники. В основном, частное и разность используются для расчетов, связанных с количественными характеристиками различных объектов.

Вычисление частного и разности производится с помощью математических операций деления и вычитания соответственно. Деление представляет собой операцию, при которой одно число делится на другое число, а результатом является частное от деления. А вычитание – это операция, при которой из одного числа вычитается другое число, и результатом является разность между ними.

Для вычисления частного нужно поделить одно число на другое число. Это можно сделать с помощью калькулятора или в ручную. В последнем случае вам нужно найти количество раз, сколько второе число умещается в первом, и записать результат в виде десятичной дроби.

Для вычисления разности нужно из большего числа вычесть меньшее число. Результатом является разность между этими числами. Если вам нужно вычислить разность между отрицательным и положительным числами или между двумя отрицательными числами, просто поменяйте знаки чисел местами и выполните вычитание.

Таким образом, вычисление частного и разности являются базовыми математическими операциями, которые используются в повседневной жизни и научных исследованиях. Важно уметь правильно выполнять данные операции, чтобы не допустить ошибок в расчетах и получить точный результат.

Практические применения частного и разности

Частное в математике находит применение во многих областях, таких как физика, экономика, статистика и т.д. Например, в экономике можно использовать понятие частного для расчета цены товара на единицу веса или объема. В физике понятие частного может применяться при расчетах скорости тела.

Разность также широко используется в различных областях науки и техники. В физике понятие разности может быть использовано для вычисления изменения скорости или ускорения тела. В химии разность может быть использована для расчета концентрации раствора. В математике понятие разности может применяться в арифметике для нахождения разницы между двумя числами.

В общем, понимание и использование понятий частного и разности имеет важное значение в различных областях науки и техники. Они позволяют решать проблемы, которые связаны с изменением величин и нахождением различий между ними.

Значение частного и разности в финансовой математике

В финансовой математике понятия частного и разности являются важными для решения задач связанных с инвестициями и финансовыми планированиями.

Частное в финансовой математике обозначает отношение между двумя величинами. Например, при расчете доходности инвестиций в акции частное выражается отношением прибыли к вложенным средствам. Частное также важно при расчете финансовых показателей, таких как коэффициент текущей ликвидности или коэффициент финансовой независимости.

Разность в финансовой математике обозначает разницу между двумя величинами. Это может быть например разница между ценой покупки и ценой продажи акций или разница между фактическим и плановым объемом продаж компании. Разность также используется для расчета изменений в финансовых показателях.

В обоих случаях, как при работе с частным, так и при работе с разностью, важно учитывать факторы, влияющие на данные величины. Например, в финансовых расчетах нередко необходимо учитывать инфляцию, валютный курс, налоговые отчисления и другие факторы, которые могут существенно изменить финансовые показатели.

Частное и разность в геометрии

В геометрии частное и разность могут быть применены для нахождения значений различных фигур и пространственных объектов.

Например, для расчета площади круга можно использовать формулу частного площади круга и квадрата со стороной радиуса: Sкруга = πr² / 4.

В случае трехмерных фигур, таких как параллелепипеды, можно использовать разность между объемом фигуры и объемом вписанного в нее тела. Например, объем пирамиды можно найти, вычислив разность между объемом пирамиды и объемом параллелепипеда, в который пирамида вписана.

Частное и разность также могут быть использованы для расчета расстояний и углов между объектами в пространстве. Например, можно вычислить расстояние между двумя точками на плоскости, используя формулу частного расстояния между точками.

В целом, частное и разность имеют широкое применение в геометрии и используются для решения различных задач и задач разной степени сложности.

Примеры использования частного и разности в криптографии

Криптография — это наука об обеспечении защиты информации. Частное и разность являются одними из основных математических концепций, используемых в криптографии. Рассмотрим некоторые примеры использования этих понятий:

1. Накопление ключей с помощью частного: В криптографии используется частное между двумя числами для создания криптографически стойкого ключа. Данный ключ используется для защиты данных и обеспечивает высокую степень их конфиденциальности.
2. Использование разности в шифровании: Шифрование данных с использованием разности производится путем выбора двух случайных чисел. Первое число является секретным ключом, а второе — сообщением пользователя. Затем секретный ключ вычитается из сообщения, и результатом является зашифрованное сообщение.
3. Решение криптографических проблем с помощью частного: Частное является ключевым понятием в криптографии и электронной подписи. Используя частное, можно решить криптографические проблемы, такие как построение криптосистем, вычисление хэш-функций, создание электронной подписи и т.д.

Таким образом, частное и разность являются важными понятиями в криптографии, которые обеспечивают защиту информации от несанкционированного доступа. Необходимость использования подобных математических концепций возникает в любой сфере, где требуется защита данных, так как они позволяют создать криптографически стойкие алгоритмы.

Особенности вычисления частного и разности в программировании

Частное и разность являются одними из основных математических операций, применяемых в программировании. Однако, вычисление этих операций в программировании имеет свои особенности.

Вычисление частного в программировании может быть осуществлено как с помощью оператора деления, так и с помощью умножения на обратное число. В первом случае, необходимо учитывать возможность деления на 0, которое может привести к ошибке выполнения программы. Во втором случае, необходимо уметь находить обратное число, что может быть нетривиальной задачей в случае больших чисел или чисел с плавающей точкой.

Вычисление разности в программировании просто осуществляется с помощью оператора вычитания. Однако, при работе с числами с плавающей точкой, могут возникнуть проблемы округления, которые могут привести к ошибкам в результате вычислений.

Также, стоит помнить, что в программировании могут использоваться различные алгоритмические методы, которые позволяют оптимизировать вычисления. Например, при работе с большими числами, может быть эффективнее использовать методы длинной арифметики вместо стандартных операций. Также, может быть полезно использовать библиотеки математических функций, которые содержат готовые реализации различных операций.

Как использовать частное и разность в химии

Частное и разность в математике могут оказаться полезными при решении задач в химии. Например, при подсчете массы реакционной смеси или вычислении процентного соотношения компонентов в растворе.

Одним из примеров использования частного и разности в химии является расчет концентрации раствора. Для этого необходимо знать массу растворителя и растворенного вещества, а также объем раствора. Массу растворенного вещества можно определить как разность массы смеси до и после растворения. Зная массу и объем растворителя, можно вычислить его плотность как частное массы на объем. И, наконец, определив плотность раствора и массу растворенного вещества, можно вычислить его концентрацию.

Еще одним примером использования частного и разности в химии является расчет массы продуктов реакции. Для этого нужно знать массу реагента и его молярную массу, а также коэффициенты стехиометрического уравнения реакции. Коэффициенты в стехиометрическом уравнении показывают, какие пропорции продуктов и реагентов участвуют в реакции. Вычислив количество молей реагента, можно вычислить количество молей продукта. Зная массу одного моля продукта, можно вычислить его массу.

Таким образом, понимание принципов частного и разности в математике может быть очень полезно для тех, кто занимается химией. Они помогают вычислять концентрацию растворов, массу реагентов и продуктов реакции, а также решать другие задачи в области химии.

Применение частного и разности на практике в медицине

Частное и разность — математические понятия, которые находят свое применение в медицине. Они позволяют обработать данные и провести точный анализ результатов.

Например, для определения эффективности лекарства применяется расчет частного. Если нужно выяснить, как быстро лекарство выводится из организма, то используется разность. Врачи также могут применять данные понятия при расчете дозировки лекарств или выявлении токсичности препаратов.

Более того, частное и разность помогают проводить исследования в медицине. Например, сравнивать эффективность различных методов лечения или выявлять статистические закономерности на основе данных о заболеваемости.

Медицина и математика имеют много общих точек контакта, и использование понятий частного и разности — только одна из них. Врачи не всегда являются математиками, но понимание основных математических концепций существенно помогает им в работе.

В целом, знание математики и умение применять ее на практике нужны не только в медицине, но и во многих других областях. Поэтому, не стоит недооценивать роль математики в нашей жизни.

Значение частного и разности в статистике

Чем полезны частное и разность в статистике? Они могут служить способом измерить разницу между значениями, например в двух разных выборках, а также определить, насколько сильно они отличаются друг от друга.

Частное может быть использовано для измерения того, как одна величина меняется относительно другой. Например, если мы исследуем среднее значение дохода в двух разных странах, мы можем использовать частное, чтобы вычислить, во сколько раз одна складывается с другой.

Разность может быть использована для измерения того, насколько близки две величины. Например, если мы сравниваем среднее значение зарплаты в двух компаниях, мы можем использовать разность, чтобы определить насколько одно значение отличается от другого.

Кроме этого, частное и разность могут быть использованы для вычисления статистических показателей, таких как коэффициент корреляции или коэффициент вариации. Они также могут помочь нам определить, насколько значимы различия в отдельных параметрах, что может быть полезно для принятия решений и определения стратегии.

В заключение, частное и разность являются важными инструментами для измерения различий между величинами и определения статистической значимости их различий. Их использование может помочь исследователям в области статистики и принимающим решения в различных сферах деятельности.

Как использовать частное и разность в повседневной жизни

Математические операции частное и разность используются не только в классе, но и в повседневной жизни. Они помогают решать множество задач, связанных с финансами, работой и домашними делами.

Финансы

• При покупке продуктов или других товаров необходимо рассчитать цену за единицу товара. Для этого нужно найти частное, поделив общую стоимость на количество единиц товара.
• При расчете процентов по кредиту или депозиту необходимо использовать разность между начальной и конечной суммой вклада.

Работа

• Для рассчета скорости движения или производительности работы необходимо найти частное между пройденным расстоянием или выполненной работой и временем, потраченным на это.
• При расчете зарплаты можно использовать разность между начисленной суммой и вычетами.

Домашние дела

• Для расчета количества необходимого материала для отделки стен или пола необходимо найти частное между площадью помещения и размерами материала.
• При расчете ежемесячных расходов на электроэнергию, газ и воду необходимо использовать разность между начальным и конечным показаниями счетчиков.

Использование частного и разности в повседневной жизни помогает не только быстро и правильно решать задачи, но и делать более обоснованные и экономически выгодные решения.

Вопрос-ответ:

Что такое частное в математике и как его вычислить?

Частное — это результат деления одного числа на другое. Для вычисления частного нужно поделить делимое на делитель. Например, частное чисел 12 и 3 равно 4 (12 / 3 = 4).

Как определить разность между двумя числами?

Разность — это результат вычитания одного числа из другого. Для определения разности нужно вычесть вычитаемое из уменьшаемого. Например, разность между числами 10 и 4 равна 6 (10 — 4 = 6).

Как связаны частное и разность в математике?

Частное и разность связаны друг с другом через умножение. Если из большего числа вычесть произведение меньшего числа и некоторого числа, то результатом будет остаток от деления большего числа на меньшее число (формула: делимое = делитель × частное + остаток). Например, 27 = 5 × 5 + 2, где 5 — это частное, 2 — это остаток.

В каких областях практически применяют частное и разность?

Частное и разность находят применение во многих областях, таких как финансы, экономика, инженерия и наука. Например, при расчете процентной ставки, при определении прибыли или убытка, при проектировании и строительстве зданий и сооружений.

Какие ошибки часто допускают при вычислении частного и разности?

Ошибки при вычислении частного и разности могут быть связаны с неправильным выбором делимого и делителя, ошибками в вычислениях и невнимательностью. Например, вместо вычитания из большего числа меньшего, можно по ошибке вычесть большее число из меньшего, что даст неправильный результат.

Можно ли использовать частное и разность для решения задач геометрии?

Да, частное и разность могут использоваться для решения задач геометрии. Например, для нахождения площади прямоугольника можно вычислить разность между длиной и шириной, а для нахождения периметра треугольника — сумму его сторон.

Как правильно округлять частное и разность?

Округление частного и разности зависит от заданной точности. Если требуется округлить до целого числа, то надо отбросить дробную часть. Если до определенного числа знаков после запятой, то нужно определить последнюю значащую цифру и округлить ее до нужного количества знаков. Например, при округлении числа 6.789 до двух знаков после запятой получится 6.79, так как третья цифра (9) больше 5.