Что такое разность и частное в математике

Разность и частное – основные понятия в математике. Разность двух чисел — это результат вычитания одного числа из другого. Частное — это результат деления одного числа на другое. Узнайте подробнее о понятиях разности и частного в математике и их применении в решении задач.

Разность и частное — две основные операции в математике, которые позволяют нам выполнять простые и сложные вычисления. Разность определяется как разница между двумя числами, а частное — результат деления одного числа на другое.

Понятие разности можно представить в виде вычитания. Например, если у нас есть два числа: 10 и 5, то разность между ними будет равна 5 (10 — 5 = 5). Разность может быть положительной или отрицательной в зависимости от того, какое число мы вычитаем из другого.

Частное, с другой стороны, определяется как результат деления одного числа на другое. Например, если у нас есть два числа: 10 и 2, то частное будет равно 5 (10 / 2 = 5). Частное также может быть положительным или отрицательным в зависимости от знаков чисел.

Важно отметить, что ноль не может быть использован в качестве делителя, так как результатом деления на ноль является неопределенность.

Разность и частное имеют множество применений в повседневной жизни и в различных областях науки, таких как физика, экономика и статистика. Они позволяют нам решать задачи, находить отклонения, проводить анализ и многое другое. Понимание этих операций является ключевым для успешного использования математических концепций и решения различных задач.

Что такое разность в математике?

Разность обозначается знаком минус (-) между вычитаемым и вычитателем. Например, если есть числа 8 и 5, то разность между ними будет равна 3 (8 — 5 = 3).

Разность можно интерпретировать как расстояние между двумя точками на числовой прямой. Если первое число больше второго, то разность будет положительной. Если первое число меньше второго, то разность будет отрицательной. Если числа равны, то разность будет равна нулю.

Разность может быть использована для решения различных задач, например, для вычисления изменения величины, измерения отклонения или нахождения расстояния между двумя точками. Она является важным инструментом в арифметике, алгебре и других областях математики.

Примеры использования разности:

• Вычисление изменения температуры: если температура утром была 10 градусов, а вечером стала 5 градусов, то разность температур будет равна -5 градусов.
• Измерение отклонения: если цель состояла в достижении 100 продаж в месяц, а фактическое количество продаж составило 80, то разность между целью и фактическим результатом будет равна -20 продаж.
• Нахождение расстояния: если точка A находится на координате 5, а точка B на координате 10, то разность между ними будет равна 5 единиц.

Понятие частного в математике

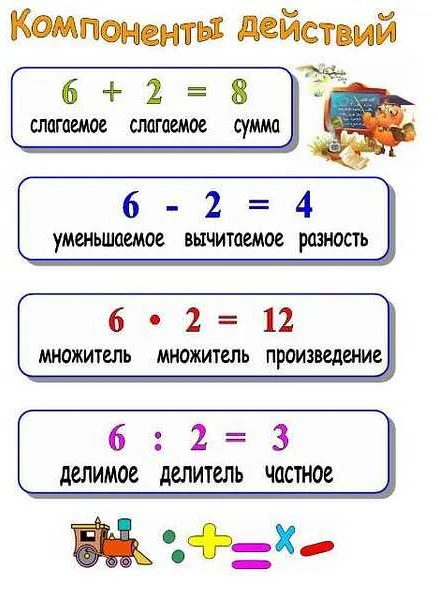
Частное может быть представлено в виде обыкновенной дроби, десятичной дроби или процента. Обычно частное округляется до определенного количества знаков после запятой.

Например, если мы разделим число 10 на число 2, то получим частное равное 5. Это означает, что число 2 содержится в числе 10 пять раз.

Частное также может быть представлено с помощью десятичной дроби. Например, если мы разделим число 1 на число 3, то получим частное равное 0.33333… (бесконечная десятичная дробь). Это означает, что число 3 содержится в числе 1 примерно 0.3333 раза.

Частное может быть положительным или отрицательным, в зависимости от знаков числителя и знаменателя. Если числитель и знаменатель имеют одинаковый знак, то частное будет положительным. Если числитель и знаменатель имеют разный знак, то частное будет отрицательным.

В математике, понятие частного используется во многих различных областях, таких как арифметика, алгебра, геометрия и т.д. Оно играет важную роль при решении задач и нахождении решений.

Разность и частное: основные отличия

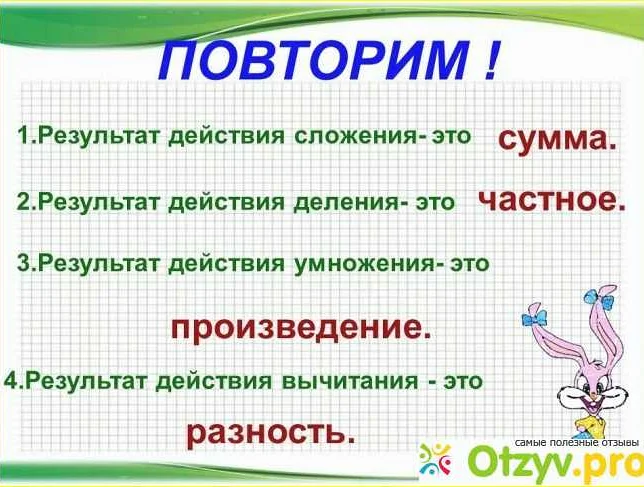
Разность относится к операции вычитания и показывает на сколько одно число отличается от другого. Например, если есть два числа — 8 и 3, то разность между ними будет равна 5. Разность может быть как положительной, так и отрицательной в зависимости от порядка чисел. Разность также может быть использована для нахождения промежуточных значений в задачах.

Частное относится к операции деления и показывает результат деления одного числа на другое. Например, если есть число 10 и его нужно разделить на число 2, то частное будет равно 5. Частное всегда положительное, если только не указано иное. Частное может быть использовано для нахождения среднего значения или расчета долей в процентах в задачах.

Таким образом, основное отличие между разностью и частным заключается в том, что разность показывает разницу между двумя числами, а частное показывает результат деления одного числа на другое. Оба понятия являются важными в математике и находят свое применение в различных сферах.

Вычисление разности: примеры

Ниже представлены примеры вычисления разности:

ПримерВычисление разности

Пример 1	7 — 3 = 4
Пример 2	15 — 9 = 6
Пример 3	23 — 12 = 11

Таким образом, разность между числами 7 и 3 равна 4, между числами 15 и 9 равна 6, а между числами 23 и 12 равна 11.

Вычисление частного: примеры

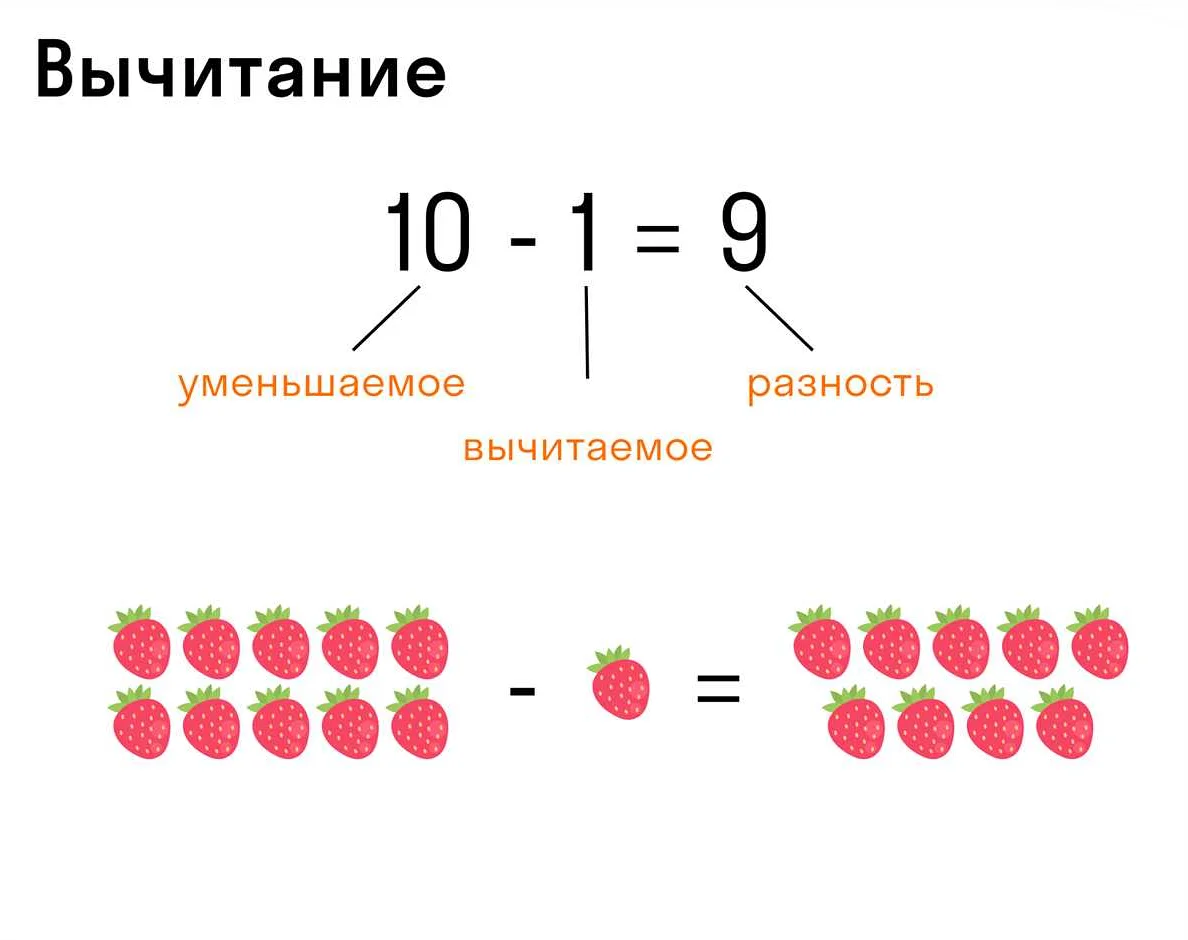
Пример 1:

Вычислить частное от деления числа 10 на число 2.

Делимое: 10

Делитель: 2

Частное: 10 / 2 = 5

Ответ: Частное равно 5.

Пример 2:

Вычислить частное от деления числа 15 на число 3.

Делимое: 15

Делитель: 3

Частное: 15 / 3 = 5

Ответ: Частное равно 5.

Пример 3:

Вычислить частное от деления числа -20 на число 4.

Делимое: -20

Делитель: 4

Частное: -20 / 4 = -5

Ответ: Частное равно -5.

Таким образом, вычисление частного является основной операцией в математике и позволяет нам делить числа на равные или неравные части.

Значение разности и частного в реальной жизни

В реальной жизни разность может быть полезна для определения изменений величин. Например, разность между текущим и предыдущим показателями температуры позволяет оценить изменение погоды. Также разность может использоваться для определения разницы во времени, расстоянии, стоимости товаров и т.д.

Частное же имеет применение во многих практических ситуациях. Например, при расчете скорости можно использовать частное между пройденным расстоянием и затраченным временем. Также частное может быть полезно при расчете среднего значения, например, среднего возраста в группе людей или среднего количества товаров, проданных за определенный период времени.

В обоих случаях разность и частное являются инструментами, которые помогают анализировать и оценивать различные величины и их изменения в реальной жизни. Они позволяют нам делать выводы, принимать решения и прогнозировать будущие события на основе математических расчетов.

Практическое применение разности в математике

Одним из практических применений разности является вычисление изменения величин, например, при анализе финансовых данных. Если у нас есть начальное значение и конечное значение некоторой величины, то разность между ними позволяет нам определить изменение этой величины за определенный период времени.

Другим примером использования разности является вычисление скорости или ускорения. Если мы знаем начальную и конечную позицию объекта, то разность между этими позициями позволяет нам определить его перемещение за определенное время. Это позволяет нам вычислить скорость, с которой объект двигается, или ускорение, с которым он меняет свою скорость.

Разность также применяется при решении задач, связанных с процентами. Например, если нам даны два значения в процентах, то разность между ними позволяет нам определить изменение величины в процентном отношении.

Кроме того, разность может использоваться для сравнения двух значений. Если у нас есть две величины, то разность между ними позволяет нам определить, насколько они отличаются друг от друга. Это может быть полезно, например, при анализе данных или при сравнении результатов экспериментов.

Таким образом, разность является важным математическим понятием, которое находит широкое применение в различных областях. Она позволяет нам вычислять изменения величин, определять скорость и ускорение, решать задачи с процентами и сравнивать значения. Знание и понимание этого понятия позволяет нам более глубоко анализировать и понимать мир вокруг нас.

Практическое применение частного в математике

Понятие частного, или деления, в математике имеет широкое практическое применение. Оно используется в различных областях науки и повседневной жизни.

В физике, например, частное применяется для расчета скорости. Если известно пройденное расстояние и время, то скорость можно найти, разделив пройденное расстояние на время.

В экономике частное используется при рассмотрении финансовых показателей. Например, при расчете прибыли предприятия используется отношение прибыли к затратам.

В медицине частное применяется при расчете дозы лекарственного препарата. Если известно общее количество препарата и необходимое количество для одной дозы, то можно найти количество доз, разделив общее количество препарата на количество для одной дозы.

Таким образом, понятие частного имеет практическое значение и находит применение в различных областях деятельности человека.

Вопрос-ответ:

Что такое разность в математике?

Разность в математике — это результат вычитания одного числа из другого. Например, разность чисел 7 и 3 равна 4.

Как вычислить разность двух чисел?

Для вычисления разности двух чисел нужно из большего числа вычесть меньшее число. Например, если у нас есть числа 10 и 5, то разность будет равна 5.

Что такое частное в математике?

Частное в математике — это результат деления одного числа на другое. Например, частное от деления числа 10 на 2 равно 5.

Как вычислить частное двух чисел?

Для вычисления частного двух чисел нужно разделить одно число на другое. Например, если у нас есть числа 12 и 3, то частное будет равно 4.

Можно ли вычислить разность или частное для дробей?

Да, можно вычислить разность или частное для дробей. Для вычисления разности дробей нужно вычесть числитель и знаменатель одной дроби из числителя и знаменателя другой дроби. А для вычисления частного дробей нужно поделить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби.

Что такое разность в математике?

Разность в математике — это результат вычитания одного числа из другого. Например, разность чисел 8 и 3 равна 5.

Видео по теме: