Что значит в математике частное

Частное в математике — это результат деления одного числа на другое. Изучение понятия частное позволяет понять, как разделять и распределять количество, а также решать задачи, связанные с долей и долевыми отношениями.

Частное — одна из основных операций в математике, которая позволяет вычислять результат деления одного числа на другое. Определение частного включает в себя два числа: делимое и делитель. Делимое — это число, которое будет делиться на другое число, называемое делителем. Результатом операции деления является частное, или quotiens, которое указывает, сколько раз делитель содержится в делимом.

Частное обладает несколькими важными свойствами. Во-первых, частное может быть положительным, отрицательным или нулевым числом, в зависимости от знаков делимого и делителя. Во-вторых, если делитель равен нулю, операция деления не определена и результатом будет бесконечность или «не число» (NaN). В-третьих, при делении нацело, когда делитель равен единице, частное равно делимому.

Частное имеет широкое применение в различных областях математики и науки. В арифметике и алгебре частное используется для решения уравнений, нахождения корней и факторизации чисел. В геометрии частное используется для вычисления площади и объемов фигур. В физике и экономике частное применяется для определения скорости, ускорения, коэффициента эффективности и других величин.

Определение частного в математике

Формально, частное двух чисел a и b определяется как число c, при котором выполняется следующее равенство:

c = a ÷ b

где a — делимое, b — делитель, c — частное.

Важно отметить, что деление на ноль запрещено в математике, поскольку не имеет смысла и приводит к неопределенности. Поэтому при выполнении деления необходимо убедиться, что делитель не равен нулю.

Частное может быть как целым числом, так и десятичной дробью, в зависимости от величины делимого и делителя. Если результат деления является целым числом, то говорят, что деление произошло без остатка.

Частное имеет ряд свойств, таких как коммутативность (порядок деления не важен), ассоциативность (результат деления не зависит от порядка скобок) и дистрибутивность (частное от суммы равно сумме частных).

Частное широко применяется в различных областях математики и науки, например, в физике, экономике, статистике и т.д. Оно позволяет решать задачи, связанные с распределением ресурсов, вычислением вероятности и многими другими.

Видео по теме:

Свойства частного в математике

СвойствоОписание

Существование	У любого действительного числа a и ненулевого числа b существует частное a/b.
Единственность	Если a/b = c/d и b и d не равны нулю, то a*d = b*c.
Ассоциативность	Для любых чисел a, b и c выполняется (a/b)/c = a/(b*c).
Коммутативность	Для любых чисел a и b выполняется a/b = b/a.
Распределительное свойство	Для любых чисел a, b и c выполняется a/(b+c) = a/b + a/c.
Отсутствие деления на ноль	Частное a/0 не определено, так как деление на ноль не имеет смысла.

Эти свойства делают частное важным понятием в математике и его применение распространено в различных областях, таких как алгебра, геометрия, физика и экономика.

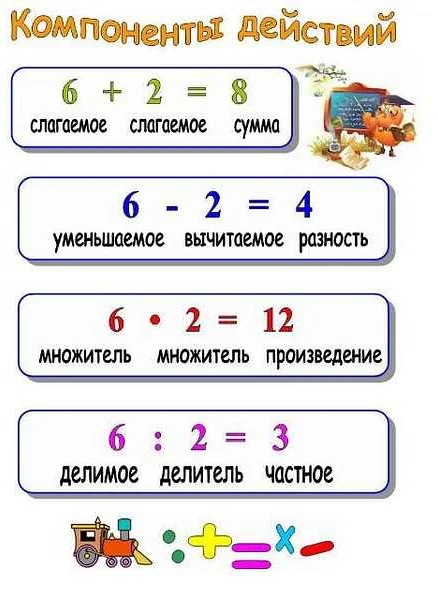
Арифметические операции с частным

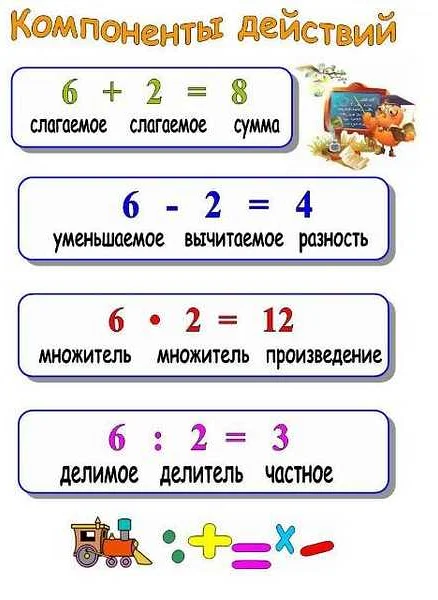
Сложение с частным — это операция, при которой к частному прибавляется другое число. Например, если имеется частное 5 и нужно прибавить 3, то результат будет равен 8.

Вычитание из частного — это операция, при которой из частного вычитается другое число. Например, если имеется частное 10 и нужно вычесть 4, то результат будет равен 6.

Умножение частного на число — это операция, при которой частное умножается на другое число. Например, если имеется частное 6 и нужно умножить его на 2, то результат будет равен 12.

Деление частного на число — это операция, при которой частное делится на другое число. Например, если имеется частное 8 и нужно разделить его на 4, то результат будет равен 2.

Арифметические операции с частным широко используются в различных областях, включая финансы, физику, статистику и программирование. Они позволяют выполнять различные вычисления и анализировать данные.

Частное и дроби

Частное представляет собой результат деления двух чисел. В математике, когда мы делим одно число на другое, получается дробь. Дробь состоит из двух чисел: числителя и знаменателя.

Числитель — это число, которое делим, а знаменатель — это число, на которое делим. Например, если мы делим число 6 на число 3, то числитель равен 6, а знаменатель равен 3.

Частное можно записать в виде десятичной дроби или обыкновенной дроби. Десятичная дробь представляет собой число с плавающей точкой, например 2.5. Обыкновенная дробь представляет собой дробное число, например 1/2.

Частное и дроби широко используются в различных областях математики и ежедневной жизни. Например, при решении задач на поиск среднего значения, при вычислении процентов, при делении денежных сумм и т.д.

Обыкновенная дробьДесятичная дробь

1/2	0.5
3/4	0.75
5/8	0.625

Изучение частного и дробей помогает нам лучше понять основы математики и применять их в реальных ситуациях. Понимая, как работает деление и как записывается его результат, мы можем решать сложные задачи и использовать математику в нашей повседневной жизни.

Применение частного в реальной жизни

1. Финансы: Частное может быть использовано для расчета процентных ставок, например, при расчете ежемесячных платежей по ипотеке или кредиту. Зная общую сумму займа и количество платежей, можно вычислить ежемесячный платеж, разделив общую сумму на количество платежей.
2. Торговля: Частное может использоваться для определения цены единицы товара. Например, расчет стоимости одного килограмма продукта или стоимости одной акции на фондовом рынке. Для этого нужно разделить общую стоимость товара на единицы, которые вы покупаете.
3. Инженерия: Частное может быть применено в различных технических расчетах, например, при определении скорости или ускорения. Разделив пройденное расстояние на время, можно найти скорость. Аналогично, разделив изменение скорости на время, можно найти ускорение.
4. Медицина: Частное может использоваться для расчета различных медицинских показателей, таких как скорость сердечных сокращений в минуту или давление крови. Разделив общее количество сердечных сокращений на время, можно найти скорость сердечных сокращений. Аналогично, разделив силу, с которой кровь давит на стенки сосудов, на площадь стенок, можно найти давление.

Все эти примеры показывают, что частное является важной математической операцией, которая находит свое применение в различных областях жизни.

Частное и производные

Частное — это результат деления одной функции на другую. Обычно обозначается как f(x)/g(x), где f(x) и g(x) — функции, а x — их аргументы. Частное позволяет определить, как меняется значение одной функции относительно значения другой функции.

Производная — это понятие, которое позволяет определить скорость изменения функции в определенной точке. Производная функции f(x) обозначается как f'(x) или df(x)/dx и определяется как предел отношения изменения функции к изменению ее аргумента при стремлении последнего к нулю.

Частное и производные тесно связаны между собой. В частности, производная частного функций f(x)/g(x) может быть выражена с помощью производных отдельных функций f'(x) и g'(x), а также с помощью самих функций f(x) и g(x).

Изучение частного и производных имеет большое значение в математическом анализе и его приложениях. Эти понятия используются для решения задач из различных областей, таких как физика, экономика, инженерия и другие. Они позволяют анализировать и предсказывать поведение функций и изучать их свойства.

ФункцияПроизводная

f(x) + g(x)	f'(x) + g'(x)
f(x) — g(x)	f'(x) — g'(x)
f(x) * g(x)	f'(x) * g(x) + f(x) * g'(x)
f(x) / g(x)	(f'(x) * g(x) — f(x) * g'(x)) / (g(x))^2

Таблица показывает связь между производными различных операций с функциями. Она позволяет находить производные сложных функций и использовать их для анализа их свойств.

Частное и статистика

Одним из примеров использования частного в статистике является расчет среднего значения или средней в статистическом наборе данных. Для этого необходимо найти сумму всех значений и поделить ее на количество значений. Таким образом, среднее значение можно рассматривать как частное суммы и количества значений.

Частное также может быть использовано для расчета других статистических показателей, таких как медиана, мода и стандартное отклонение. Например, при расчете медианы, необходимо упорядочить все значения по возрастанию или убыванию и найти значение, которое находится в середине. Если количество значений нечетное, то медиана будет являться значением в середине, если количество значений четное, то медиана будет равна среднему арифметическому двух значений в середине. Таким образом, медиана может быть рассмотрена как частное двух значений в середине.

Частное также может быть использовано для сравнения и оценки данных в статистическом исследовании. Например, если необходимо сравнить различные группы или выборки данных, можно вычислить частные показателей для каждой группы и сравнить их между собой. Это помогает определить различия и сходства между группами и сделать выводы на основе этих данных.

Таким образом, частное играет важную роль в статистике и позволяет проводить различные анализы и оценки данных. Оно является одним из основных математических понятий, которое помогает в понимании и измерении различных параметров в статистическом исследовании.

Примеры задач с частным

1. 1. Задача 1: Дано число 15. Разделите его на 3. Какое будет частное?

Решение: Для решения данной задачи нужно разделить число 15 на 3. Получаем частное равное 5.

1. 1. Задача 2: В магазине есть 24 яблока. Их нужно разложить поровну по 6 подарочным коробкам. Сколько яблок будет в каждой коробке?

Решение: Для решения данной задачи нужно разделить число 24 на 6. Получаем частное равное 4. В каждой коробке будет по 4 яблока.

1. 1. Задача 3: Вася собрал 54 шарика из разных цветов. Он хочет разделить их поровну между собой и своим другом Петей. Сколько шариков получит каждый ребенок?

Решение: Для решения данной задачи нужно разделить число 54 на 2. Получаем частное равное 27. Каждый ребенок получит по 27 шариков.

Таким образом, понимание понятия частного позволяет решать различные задачи, связанные с делением и распределением ресурсов.

Вопрос-ответ:

Что такое частное в математике?

Частное в математике — это результат деления одного числа на другое. В математической записи частное обозначается символом «/», например, 5/2. Частное показывает, сколько раз одно число содержится в другом.

Какие свойства имеет частное в математике?

Частное обладает несколькими важными свойствами. Во-первых, если число делится на 1, то частное будет равно самому числу. Во-вторых, частное от деления числа на само себя всегда равно 1. Также, если два числа делятся на одно и то же число, то их частные будут равны. Например, если 10 и 20 делятся на 5, то их частные 2 и 4 также будут равны.

Где применяют частное в математике?

Частное используется во многих областях математики и повседневной жизни. Например, в финансовых расчетах частное используется для определения процента или расчета доли. В геометрии частное используется для определения углов, площадей или объемов фигур. Также, частное может быть полезно для решения задач по пропорциям или нахождению среднего значения.

Как найти частное двух чисел?

Чтобы найти частное двух чисел, нужно разделить одно число на другое. Для этого можно использовать операцию деления или десятичную запись. Например, чтобы найти частное чисел 10 и 2, нужно разделить 10 на 2, что даст результат 5. Также можно записать это как 10/2 = 5.