Частное в математике что такое
Содержимое
- 1 Частное в математике что такое
- 1.1 Что такое частное в математике?
- 1.2 Определение и основные понятия
- 1.3 Примеры частного в математике
- 1.4 Роль частного в различных областях
- 1.5 Значение частного в науке и технике
- 1.6 Как вычислить частное чисел
- 1.7 Свойства частного в математике
- 1.8 Вопрос-ответ:
- 1.9 Применение частного в реальной жизни
- 1.10 Видео по теме:
Частное в математике — это результат деления одного числа на другое. В статье рассмотрены основные понятия и примеры вычисления частного чисел. Узнайте, как использовать частное в математических операциях и решении задач.
Частное — это одна из основных операций в математике, которая позволяет нам делить одно число на другое. Частное обозначается символом «/», и результат деления двух чисел называется также частным. Частное может быть как целым числом, так и десятичной дробью, в зависимости от чисел, которые мы делим.
Для понимания частного важно знать, что одно число делится на другое, если результат деления является целым числом без остатка. Например, если мы делим 10 на 2, то получаем частное 5, потому что 10 делится на 2 без остатка. В этом случае частное будет целым числом.
Однако, если результат деления числа на другое число не является целым числом, то мы получаем десятичную дробь в качестве частного. Например, если мы делим 10 на 3, то получаем частное около 3.33333 и так далее. В этом случае частное является десятичной дробью.
Примеры деления:
Пример 1: 12 / 4 = 3
Пример 2: 15 / 2 = 7.5
Пример 3: 20 / 3 = 6.66666…
Частное является важным понятием в математике и используется во многих областях, таких как физика, экономика, статистика и т.д. Понимание частного позволяет нам решать сложные задачи и анализировать данные, основываясь на результате деления чисел.
Что такое частное в математике?

Частное может быть представлено в виде десятичной дроби или десятичной разложения, а также в виде обыкновенной дроби. Обычно, при делении двух чисел, одно из них называется делимым, а другое — делителем.
В математике, частное часто используется для решения проблем, связанных с распределением и сравнением ресурсов, времени, длины и т.д. Например, если у вас есть 10 яблок и вы хотите равномерно поделить их между 2 детьми, вы можете использовать операцию деления, чтобы найти сколько яблок получит каждый ребенок.
Частное также может быть использовано для нахождения среднего значения (среднего арифметического) ряда чисел. В этом случае, сумма всех чисел делится на их количество.
ПримерВычисление
| 10 / 2 | 5 |
| 20 / 4 | 5 |
| 15 / 3 | 5 |
Таким образом, частное является важным понятием в математике, которое используется для деления чисел и решения различных задач.
Определение и основные понятия
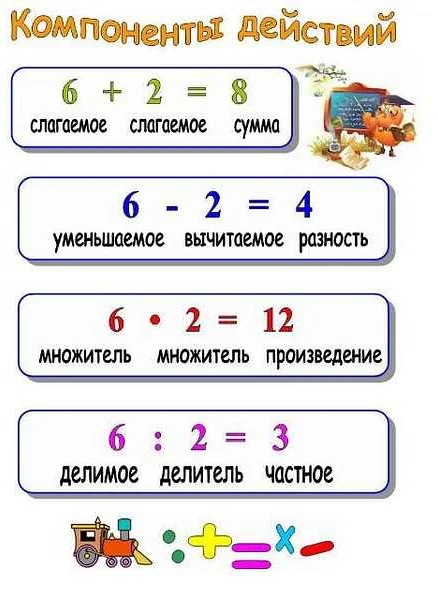
Делимое — это число, которое делится на другое число. Например, в выражении «10 ÷ 2», число 10 является делимым.
Делитель — это число, на которое делится другое число. В примере выше, число 2 является делителем.
Частное — это результат деления делимого на делитель. В примере «10 ÷ 2», результатом деления является число 5.
Частное может быть как целым числом, так и дробным. Например, «10 ÷ 3» равно 3.33333 и является дробным частным.
Одна из основных особенностей частного является то, что оно может быть равно бесконечности. Например, «1 ÷ 0» не имеет определенного значения и равно бесконечности.
Частное также может быть выражено в виде десятичной дроби или процента. Например, результат деления «3 ÷ 4» равен 0.75 или 75%.
Примеры частного в математике

Пример 1: Разделим число 10 на число 2.
Чтобы найти частное, мы делим делимое на делитель. В данном случае:
10 ÷ 2 = 5
Частное равно 5.
Пример 2: Разделим число 15 на число 3.
Также, чтобы найти частное, делим делимое на делитель:
15 ÷ 3 = 5
Частное равно 5.
Пример 3: Разделим число 25 на число 5.
Продолжая ту же логику, делим делимое на делитель:
25 ÷ 5 = 5
Частное равно 5.
Таким образом, во всех примерах частное равно 5. Это связано с тем, что в каждом случае делимое делится на делитель без остатка. Однако, в общем случае частное может быть и нецелым числом, если делимое не делится на делитель без остатка.
Роль частного в различных областях

1. Арифметика: В арифметике частное используется для деления одного числа на другое, что позволяет определить, сколько раз одно число содержится в другом. Это позволяет решать различные задачи, связанные с распределением ресурсов или определением долей величин.
2. Алгебра: В алгебре частное используется для решения уравнений и систем уравнений. Путем нахождения частного можно определить значения переменных и найти решение задачи.
3. Геометрия: В геометрии частное используется для определения отношений между различными геометрическими объектами. Например, отношение площадей двух фигур или отношение длин отрезков.
4. Вероятность и статистика: Вероятность и статистика тесно связаны с понятием частного. Частное позволяет определить вероятность наступления события, а также выполнить статистический анализ данных.
5. Физика и инженерия: В физике и инженерии частное используется для определения различных величин, таких как скорость, ускорение, сила и другие физические параметры. Также частное позволяет находить значения коэффициентов и проводить различные расчеты.
Таким образом, частное играет существенную роль в различных областях, позволяя решать задачи, определять отношения и находить значения различных величин.
Значение частного в науке и технике
Например, в физике частное может использоваться для вычисления скорости, ускорения или других характеристик движения объектов. Также, в электротехнике и электронике частное может быть применено для определения сопротивления, тока или напряжения в электрической цепи.
В инженерии и строительстве частное может быть использовано для вычисления прочности материалов, коэффициента сопротивления или других параметров конструкций. Благодаря частному можно определить оптимальные параметры для создания эффективных и надежных систем и механизмов.
Также, в экономике и финансовой сфере частное может использоваться для вычисления различных показателей, таких как доходность инвестиций, рентабельность предприятия или стоимость товаров и услуг.
В целом, частное имеет широкое применение в науке и технике, позволяя решать разнообразные задачи и делать количественные оценки. Без понимания и использования частного было бы сложно сделать точные измерения, провести анализ и принять взвешенные решения в различных областях деятельности.
Как вычислить частное чисел
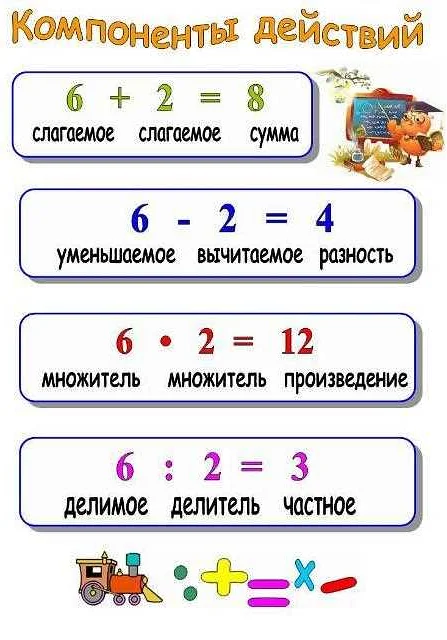
Для вычисления частного двух чисел нужно разделить делимое на делитель. Частное обозначается символом «/» или написанием делимого перед делителем.
Например, если нужно вычислить частное чисел 10 и 2, то необходимо разделить 10 на 2:
10 / 2 = 5
Таким образом, частное чисел 10 и 2 равно 5.
Если делитель равен нулю, то частное не существует, так как невозможно разделить на ноль. В таком случае говорят о «делении на ноль», что является математической ошибкой.
Также важно помнить о порядке операций при вычислении частного. Если в выражении есть другие операции, такие как умножение или сложение, то их нужно выполнить перед делением.
Например:
10 + 5 * 2 / 2 = 15
Сначала выполняется умножение 5 * 2, затем деление на 2 и, наконец, сложение с 10. Результат равен 15.
Использование скобок позволяет управлять порядком операций и вычислять частное согласно заданным правилам.
Например:
(10 + 5) * 2 / 2 = 15
В данном случае скобки указывают, что сначала нужно выполнить сложение 10 + 5, затем умножить на 2, а затем разделить на 2. Результат также равен 15.
Свойства частного в математике
Вот основные свойства частного:
| Свойство | Описание |
| Закон ассоциативности | Порядок скобок в выражении не влияет на результат деления. Другими словами, результат деления скобочного выражения не зависит от того, в каком порядке производятся операции деления. |
| Закон коммутативности | Порядок чисел в выражении также не влияет на результат деления. То есть, частное от деления одного числа на другое будет таким же, как и частное от деления другого числа на первое. |
| Закон дистрибутивности | Частное от деления суммы двух чисел на третье число будет равно сумме частного от деления каждого из этих чисел на третье число. То есть, можно разделить каждое слагаемое на третье число и затем сложить результаты. |
| Закон единицы | Частное от деления числа на единицу равно самому числу. Это свойство следует из определения частного как результат деления одного числа на другое. |
| Закон нуля | Частное от деления нуля на любое число равно нулю. Деление на ноль неопределено, поэтому нельзя выполнить это действие. |
Знание этих свойств поможет упростить вычисления и решить различные задачи, связанные с частным в математике.
Вопрос-ответ:
Что такое частное в математике?
Частное в математике — это результат деления одного числа на другое. Оно показывает, сколько раз одно число содержится в другом.
Как определить частное?
Чтобы определить частное, нужно разделить одно число на другое. Деление производится путем вычитания множителя из делимого до тех пор, пока результат вычитания не станет меньше делителя. Частное будет равно количеству вычитаний, а остаток — разнице между последним вычитанием и делителем.
Какие примеры частного можно привести?
Примеры частного можно привести из разных областей математики. Например, при делении 10 на 2, частное будет равно 5. При делении 16 на 4, частное будет равно 4. Также, можно рассмотреть примеры из области алгебры, геометрии и других разделов математики.
В каких задачах можно использовать понятие частного?
Понятие частного используется в различных типах задач. Например, в задачах на деление целых чисел, задачах на распределение предметов поровну между людьми, задачах на нахождение среднего значения и во многих других. Частное позволяет получить точные результаты и решить множество математических задач.
Применение частного в реальной жизни
Одним из примеров применения частного может быть расчет среднего значения. Например, если у нас есть набор данных, представляющих средний ежемесячный доход нескольких сотрудников, мы можем найти среднее значение этого набора, разделив сумму всех доходов на количество сотрудников.
Еще одним примером применения частного является расчет скорости движения. Например, если мы знаем расстояние, которое проехал автомобиль, и время, потраченное на это, мы можем найти скорость, разделив расстояние на время.
Частное также может использоваться для расчета долей. Например, если у нас есть некоторое количество продуктов разных видов, мы можем найти долю каждого вида, разделив количество этого вида на общее количество продуктов.
Таким образом, частное является полезным понятием, которое помогает нам решать практические задачи и делать выводы на основе числовых данных. Оно позволяет нам измерять, сравнивать и делить ресурсы и количества, что делает его неотъемлемой частью реальной жизни.




Частное в математике – это результат деления одного числа на другое. Оно позволяет нам определить, сколько раз одно число содержится в другом. Например, если у нас есть 12 яблок и мы хотим разделить их поровну между 4 детьми, то частное будет равно 3. Частное может быть как целым числом, так и десятичной дробью. В первом случае оно показывает, сколько целых частей содержит делитель в делимом числе. Во втором случае оно показывает, сколько единиц делителя содержится в делимом числе. Например, если мы делим 9 на 4, получаем 2 с остатком 1. В этом случае частное равно 2, а остаток – 1. То есть, 4 умещается в 9 два раза целым числом и еще один раз с остатком. Частное играет важную роль в различных областях математики и науки. В экономике, например, частное используется для расчета среднего дохода на человека или средней стоимости товара. В физике оно помогает определить скорость или плотность объекта. Все это делает понятие частного очень полезным и широко применяемым в нашей повседневной жизни.
Частное — это одно из основных понятий в математике, которое используется для описания отношения между двумя числами. В основном, это отношение выражается в виде деления одного числа на другое. Частное можно интерпретировать как результат деления или как долю, которую одно число составляет от другого. В математике частное часто используется для решения различных задач. Например, если нам нужно разделить 10 яблок между 2 друзьями, мы можем использовать понятие частного, чтобы найти сколько яблок достанется каждому другу. В этом случае, число 10 будет делимым, а число 2 — делителем. Чтобы найти результат, достаточно разделить 10 на 2, что дает нам частное, равное 5. Таким образом, каждому другу достанется по 5 яблок. Частное также может быть представлено в виде десятичной дроби или в виде процента. Например, если мы разделим 1 на 3, то получим десятичную дробь 0,3333… или 33,33…% в виде процента. Однако, стоит помнить, что частное не всегда является точным числом. Например, если мы разделим 7 на 2, то получим число 3,5. В этом случае, числа 7 и 2 не делятся нацело, поэтому результат будет представлен в виде десятичной дроби. Таким образом, частное — это важное понятие в математике, которое помогает нам решать задачи деления и находить доли относительно других чисел. Без частного было бы трудно представить себе мир математики и его практическое применение в повседневной жизни.
Статья очень понравилась! Я всегда увлекалась математикой, и разделение чисел на частные и общие всегда вызывало у меня интерес. Автор очень хорошо объяснил понятие «частное» и его значение в математике. Примеры, приведенные в статье, помогли мне лучше понять, как работает деление и как находить частное. Теперь я точно знаю, что частное — это результат деления одного числа на другое. Но самое интересное, что автор показал, как частное может быть использовано в реальной жизни. Например, при делении 10 пирожков между 2 друзьями, каждый получит по 5 пирожков. Это простой, но очень наглядный пример, который помогает понять, как использовать частное в повседневных ситуациях. Статья отлично дополняет мои знания о математике и помогает лучше понять это интересное и важное разделение чисел. Благодарю автора за простое и понятное объяснение!