Чем отличается математика от геометрии

Математика и геометрия являются разными отраслями науки, хотя и тесно связаны между собой. Математика изучает абстрактные структуры, законы и отношения чисел и символов, в то время как геометрия фокусируется на изучении фигур, их размеров, форм и взаимодействий. В отличие от математики, геометрия включает визуальные представления и использует понятия пространства и геометрических фигур для решения задач и построения доказательств. Обе науки важны и широко применяются в различных областях знания и практической деятельности.

Математика и геометрия являются двумя основными разделами науки, которые изучают отношения и свойства чисел и форм. Однако, несмотря на то, что математика и геометрия тесно связаны, они имеют свои специфические особенности и принципы.

Математика — это наука, изучающая структуру, пространство, количества и изменения. Она включает в себя такие разделы, как алгебра, арифметика, геометрия, математический анализ и теория вероятностей. Математика используется для анализа и объяснения явлений в различных областях науки, техники и экономики. Она основывается на строгих математических доказательствах и логических рассуждениях.

Геометрия, с другой стороны, фокусируется на изучении форм, размеров, отношений и свойств фигур и пространства. Она изучает геометрические фигуры, такие как точки, линии, плоскости, углы, многоугольники, окружности и тела. Геометрия используется для решения задач, связанных с расстояниями, площадями, объемами и другими характеристиками геометрических объектов.

Основное отличие между математикой и геометрией состоит в том, что математика является более общей наукой, которая изучает различные аспекты количественных и структурных свойств, в то время как геометрия сосредоточена на изучении форм и пространственных отношений.

Основные различия между математикой и геометрией

МатематикаГеометрия

Изучает абстрактные объекты, такие как числа, символы и операции над ними.	Изучает геометрические фигуры, пространства и взаимоотношения между ними.
Основана на формальных логических системах и аксиоматических методах.	Основана на геометрических принципах, аксиомах и доказательствах.
Изучает различные области математики, такие как алгебра, геометрия, анализ и теория вероятностей.	Изучает различные области геометрии, такие как евклидова геометрия, аналитическая геометрия и топология.
Используется для решения различных проблем и моделирования реальных ситуаций.	Используется для изучения форм и пространственных отношений в реальном мире.

Хотя математика и геометрия имеют свои отличия, они также взаимосвязаны и взаимозависимы. Математика является широкой дисциплиной, включающей в себя геометрию, в то время как геометрия является одной из важных областей математики.

Объекты изучения

Математика и геометрия имеют разные объекты изучения. В математике исследуются абстрактные объекты, такие как числа, операции, уравнения, функции и теории. Она занимается анализом и формализацией различных структур и законов, которые применяются во многих областях науки и техники.

С другой стороны, геометрия изучает пространственные объекты, такие как точки, линии, плоскости, углы, фигуры и тела. Она исследует их свойства, взаимное расположение и возможные преобразования. Геометрия развивается вокруг пространственного воображения и способности визуально представлять объекты и их отношения.

Математика и геометрия тесно взаимосвязаны, и многие математические концепции могут быть применены и в геометрии, и в других областях науки. Например, алгебраические методы могут использоваться для решения геометрических задач, а геометрические преобразования могут быть представлены и анализированы с помощью математических моделей.

Таким образом, основной разницей между математикой и геометрией является объект изучения. Математика является более абстрактной наукой, исследующей общие математические законы, тогда как геометрия фокусируется на изучении пространственных объектов и их взаимоотношений.

Методы и подходы

В математике используются различные методы, такие как анализ, алгебра, теория вероятностей и т.д. Математики решают проблемы, используя логическое мышление, формализацию и доказательства. Они стремятся к общности и точности в своих результатах и изучают различные структуры и законы, которые могут быть применены в разных областях.

Геометрия, с другой стороны, использует геометрические методы и подходы для изучения пространства, форм и отношений. Геометры обращают внимание на связи между фигурами и свойствами пространства. Они изучают геометрические формы, такие как линии, точки, плоскости и тела, и исследуют их свойства и взаимодействия.

Однако, несмотря на различия в методах и подходах, математика и геометрия тесно связаны друг с другом. Геометрия часто использует математические методы и концепты для решения своих задач, а математика использует геометрию как одну из своих областей исследования. Обе науки взаимно дополняют друг друга и способствуют более глубокому пониманию математических и геометрических проблем.

МатематикаГеометрия

Абстрактная и общая наука	Изучение форм и пространства
Использует методы анализа, алгебры и теории вероятностей	Использует геометрические методы и подходы
Логическое мышление, формализация и доказательства	Изучение связей между фигурами и свойствами пространства
Стремится к общности и точности	Изучает геометрические формы и их свойства
Изучает различные структуры и законы	Исследует геометрические свойства и взаимодействия

Принципы построения

Математика и геометрия имеют свои основные принципы построения, которые отличают их друг от друга:

1. Математика:

Математика строится на абстрактных концепциях и символах. Её принципы построения включают:

— Аксиомы и определения: математические объекты и отношения формализуются с помощью аксиом и определений.

— Логическое рассуждение: математика использует логические операции, чтобы извлекать новые знания из аксиом.

— Доказательства: математические утверждения должны быть доказаны с использованием формальных логических методов.

— Абстракция: математика стремится обобщать и абстрагировать конкретные примеры, чтобы найти общие закономерности.

2. Геометрия:

Геометрия, с другой стороны, основана на изучении форм, размеров и отношений физических объектов. Принципы построения геометрии включают:

— Изображения: геометрия использует изображения и диаграммы для визуализации геометрических объектов.

— Меры и размеры: геометрия изучает длины, углы и другие меры для определения отношений между объектами.

— Пространство: геометрия основана на понятии пространства и его свойствах, таких как симметрия и параллельность.

— Геометрические преобразования: геометрия исследует преобразования фигур, такие как повороты, сжатия и отражения.

Таким образом, математика и геометрия имеют разные принципы построения, связанные с абстрактными концепциями и символами в математике и изучением форм и размеров в геометрии.

Основные дисциплины

Математика — это наука, изучающая структуру, свойства и взаимоотношения чисел и величин. Основные дисциплины математики включают алгебру, геометрию, математический анализ, теорию вероятностей и математическую логику.

Алгебра — это раздел математики, который изучает арифметические операции над символами и их свойства. Она является основой для многих других математических дисциплин и применяется в различных областях, включая физику, экономику и информатику.

Геометрия — это наука, изучающая свойства и отношения пространственных фигур. Основные дисциплины геометрии включают евклидову геометрию, аналитическую геометрию, проективную геометрию и дифференциальную геометрию.

Евклидова геометрия — это классическая геометрия, основанная на принципах Евклида. Она изучает свойства точек, линий, плоскостей и пространственных фигур, таких как треугольники и окружности.

Аналитическая геометрия — это раздел геометрии, который использует алгебраические методы для изучения геометрических объектов. Она связывает геометрию и алгебру, позволяя решать геометрические задачи с помощью алгебраических уравнений и координат.

Проективная геометрия — это раздел геометрии, который изучает преобразования и свойства фигур, сохраняющие прямые и отношения между точками. Она имеет широкое применение в графике, компьютерном зрении и проективной геометрии.

Дифференциальная геометрия — это раздел геометрии, который изучает гладкие многообразия и свойства, определяемые на них. Она является основой для теории относительности и других областей математики и физики.

Таким образом, математика и геометрия имеют много общих принципов и взаимосвязей, но каждая из них имеет свои уникальные особенности и области применения.

Практическое применение

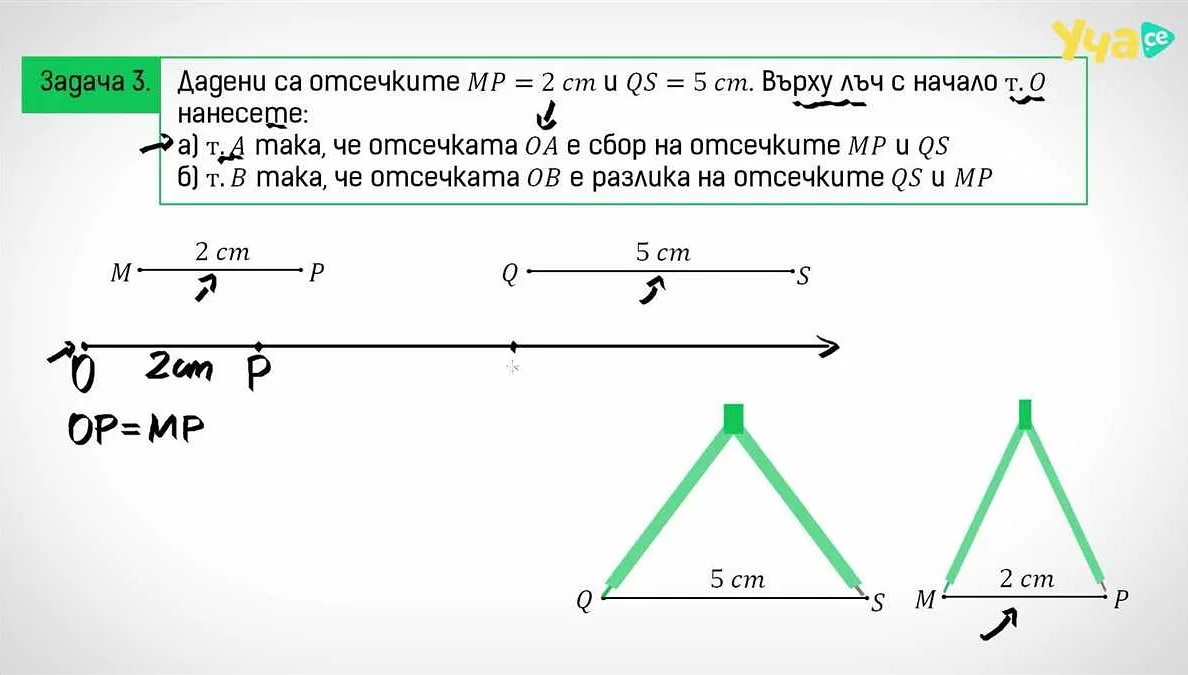
Математика и геометрия имеют широкое практическое применение в различных областях науки, техники и повседневной жизни.

• Математика применяется в физике для моделирования и решения различных физических задач. Например, с помощью математических методов можно предсказать траекторию движения тела, рассчитать скорость и ускорение.
• Геометрия используется в архитектуре для создания и проектирования зданий. С ее помощью можно рассчитать прочность конструкций, определить оптимальные размеры и форму объектов.
• Математика применяется в экономике для анализа данных, прогнозирования тенденций и оптимизации бизнес-процессов. Например, с помощью математических моделей можно определить оптимальное распределение ресурсов или рассчитать стоимость товара.
• Геометрия находит применение в компьютерной графике и визуализации данных. С ее помощью можно создавать трехмерные модели объектов, а также рассчитывать освещение и тени.
• Математика используется в медицине для анализа медицинских данных, моделирования распространения болезней и оптимизации лечения. Например, с помощью математических моделей можно определить оптимальную дозировку лекарств.

Это лишь некоторые примеры практического применения математики и геометрии. Обе дисциплины являются неотъемлемой частью нашей жизни и позволяют нам более глубоко понимать и описывать окружающий мир.

Абстрактность и конкретность

В отличие от геометрии, которая изучает пространственные фигуры и их свойства, математика более абстрактна и универсальна.

Она исследует числа, структуры, операции и отношения между ними, не ограничиваясь только геометрическими объектами.

Математика стремится к обобщенным выводам, формулам и законам, которые могут применяться в различных сферах знания и решении разнообразных проблем.

Геометрия, в свою очередь, более конкретна и ориентирована на пространственные представления.

Она изучает фигуры, их формы, размеры, свойства и взаимные отношения.

Геометрия рассматривает конкретные объекты и строит на их основе доказательства и теории.

Несмотря на отличия, математика и геометрия тесно взаимосвязаны и взаимодополняют друг друга, обеспечивая широкий спектр знаний и инструментов для научных исследований и прикладных задач.

Область применимости

Математика позволяет выражать и формализовывать различные концепции и идеи. Она помогает в анализе данных, моделировании явлений, прогнозировании и принятии решений. Математические методы используются для решения сложных проблем и оптимизации процессов.

Геометрия имеет свою уникальную область применения. Она изучает форму, размеры, относительное положение и свойства геометрических фигур и пространственных объектов. Геометрические знания и навыки применяются в архитектуре, инженерии, картографии, компьютерной графике, дизайне и других областях, где важно визуальное представление и конструктивная точность.

Геометрия позволяет строить и анализировать модели движения тел, оптимизировать конструкции, рассчитывать площади и объемы объектов, создавать точные карты и диаграммы. Она дает возможность визуализировать и понимать пространственную структуру предметов и явлений.

Таким образом, математика и геометрия имеют различные области применения, но вместе они обогащают наше понимание мира и помогают решать сложные задачи в различных сферах деятельности.

Взаимосвязь с другими науками

Математика является языком, на котором формулируются законы физики. Она позволяет описывать и объяснять различные физические явления с помощью уравнений и моделей. Без математики невозможно было бы разработать теорию относительности или квантовую механику.

Геометрия также играет важную роль в физике, особенно в теории относительности. Она помогает описывать геометрические свойства пространства и времени, а также предсказывать и объяснять гравитационные явления.

В инженерных науках математика используется для проектирования и анализа различных технических систем. Она позволяет оптимизировать параметры системы, предсказывать ее поведение и решать различные технические задачи.

Информатика и компьютерные науки также не обходятся без математики. Она является основой для разработки алгоритмов и структур данных, а также для анализа сложности алгоритмов. Математика также используется в криптографии, искусственном интеллекте и других областях информатики.

Наконец, экономика тесно связана с математикой и статистикой. Математические модели позволяют анализировать экономические процессы, прогнозировать их развитие и принимать обоснованные экономические решения. Особенно важным инструментом в экономике является теория игр, которая изучает стратегии и принятие решений в конкурентной среде.

Таким образом, математика и геометрия имеют широкую область применения и играют важную роль во многих научных и практических областях. Они являются неотъемлемой частью современного мира и являются основой для развития других наук и технологий.

Вопрос-ответ:

В чем основные различия между математикой и геометрией?

Основное различие между математикой и геометрией заключается в том, что математика является более общей наукой, которая изучает абстрактные объекты и их отношения, в то время как геометрия фокусируется на изучении пространственных форм и их свойств.

В чем состоит основной принцип математики?

Основной принцип математики заключается в строгой логической построенности и доказательности. Математика строится на основе аксиоматической системы, где каждое утверждение должно быть доказано с помощью логических рассуждений.

Какие основные принципы лежат в основе геометрии?

В основе геометрии лежат такие принципы, как понятие пространства, отношения между точками, прямыми и плоскостью, а также аксиомы, на основе которых строятся доказательства геометрических теорем. Геометрия также использует методы визуализации и доказательства с помощью рисунков и графиков.

Какие области математики могут быть связаны с геометрией?

Геометрия может быть связана с различными областями математики, такими как алгебра, теория чисел, анализ и топология. Например, алгебраическая геометрия изучает геометрические объекты, определяемые алгебраическими уравнениями, а дифференциальная геометрия изучает гладкие поверхности и кривые с помощью методов дифференциального исчисления.

Каковы практические применения математики и геометрии в реальной жизни?

Математика и геометрия имеют широкий спектр практических применений в реальной жизни. Они используются в инженерии, архитектуре, компьютерной графике, физике, экономике, биологии и других областях науки и техники. Например, геометрия позволяет строить точные планы и чертежи зданий, а математические модели используются для прогнозирования и оптимизации процессов.

Чем отличается математика от геометрии?

Математика и геометрия — это две взаимосвязанные науки, однако у них есть свои отличия. Математика изучает абстрактные структуры, формулы и законы, которые применяются в различных областях науки. Геометрия же фокусируется на изучении фигур, пространства и их свойств. Основное отличие между математикой и геометрией заключается в том, что математика более широкая наука, включающая в себя геометрию как одну из своих ветвей.

Какие основные различия и принципы есть у математики и геометрии?

Основное различие между математикой и геометрией заключается в том, что математика это широкая наука, включающая в себя различные области, включая геометрию. Геометрия же фокусируется на изучении фигур, пространства и их свойств. Принципы математики включают в себя логическую аксиому и доказательство теорем, которые строятся на основе уже известных утверждений. Принципы геометрии включают аксиомы Евклида, которые определяют основные свойства пространства и фигур.

Видео по теме: