Что такое абстрактность в математике
Содержимое
- 1 Что такое абстрактность в математике
- 1.1 Важность абстрактности в математике
- 1.2 Определение абстрактности в математике
- 1.3 Примеры абстрактных концепций в математике
- 1.4 Взаимосвязь абстрактности с другими математическими понятиями
- 1.5 Роль абстрактности в развитии математической мысли
- 1.6 Применение абстрактности в реальных задачах и науке
- 1.7 Критика и противоречия в использовании абстрактных концепций
- 1.8 Вопрос-ответ:
- 1.8.0.1 Как можно определить понятие абстрактности в математике?
- 1.8.0.2 Какие основные концепции связаны с абстрактностью в математике?
- 1.8.0.3 Какие примеры абстрактности можно привести в математике?
- 1.8.0.4 Что такое абстрактность в математике?
- 1.8.0.5 Какие основные концепции связаны с абстрактностью в математике?
- 1.8.0.6 Можете привести примеры абстрактных концепций в математике?
- 1.9 Различия в понимании абстрактности в разных математических школах и направлениях
- 1.10 Видео по теме:
Абстрактность в математике — это понятие, которое описывает способность математической абстракции моделировать реальные явления и объекты. Она позволяет ученым создавать универсальные правила и законы, которые применимы к различным областям знания и исследования. Абстрактность является одной из основных характеристик математики и является неотъемлемой частью ее развития и применения.
Абстрактность — одно из важнейших понятий в математике. Это концепция, которая позволяет упрощать и обобщать сложные явления и объекты, а также выделять общие свойства и закономерности. Благодаря абстрактности математики создают модели и теории, которые затем применяются в различных областях науки и техники.
В математике абстрактность проявляется в образовании понятий, которые не имеют прямого отношения к конкретным объектам реального мира. Например, понятие числа – это абстрактный объект, который используется для измерения и сравнения количества. Числа могут быть положительными или отрицательными, целыми или дробными, натуральными или иррациональными. Все эти различные виды чисел абстрактны, потому что они не имеют прямого соответствия с какими-либо конкретными объектами в реальном мире.
Абстракция – это процесс выделения существенных характеристик объекта и отбрасывания несущественных деталей. Например, если мы рассматриваем множество разных геометрических фигур, мы можем абстрагироваться от их формы и цвета, и сосредоточиться только на их геометрических свойствах, таких как площадь, периметр и радиус. Таким образом, абстракция позволяет нам сосредоточиться на существенных аспектах объекта и разрабатывать общие принципы и теории, которые применимы ко многим объектам.
Примером абстрактности в математике может служить концепция вектора. Вектор – это абстрактный объект, который имеет определенное направление и длину, но не имеет начала или конца. Векторы могут быть представлены числами или символами, но они не имеют непосредственного соответствия с конкретными геометрическими объектами в пространстве. Тем не менее, векторы являются мощным инструментом для решения различных математических и физических задач, таких как определение направления движения тела, расчет силы и скорости.
Важность абстрактности в математике
Абстрактность позволяет математикам увидеть общие закономерности и связи между различными математическими объектами. Она помогает в создании абстрактных моделей, которые могут быть использованы для решения конкретных проблем и задач. Благодаря абстрактности математические концепции и теории могут быть обобщены и применены в различных областях науки и техники.
Абстракция также позволяет математикам строить формальные системы, в которых все определения и правила являются четкими и точными. Это обеспечивает строгую логическую базу для развития математического знания и позволяет изучать его внутреннюю структуру и свойства.
Общность и универсальность абстрактных математических концепций позволяют использовать их не только в математике самой по себе, но и в других науках. Математические абстракции находят применение в физике, экономике, компьютерных науках и других областях, где они позволяют описывать и анализировать сложные системы и явления.
Таким образом, абстрактность играет фундаментальную роль в математике, обеспечивая точность, обобщение и применимость математических концепций в различных областях знания.
Определение абстрактности в математике
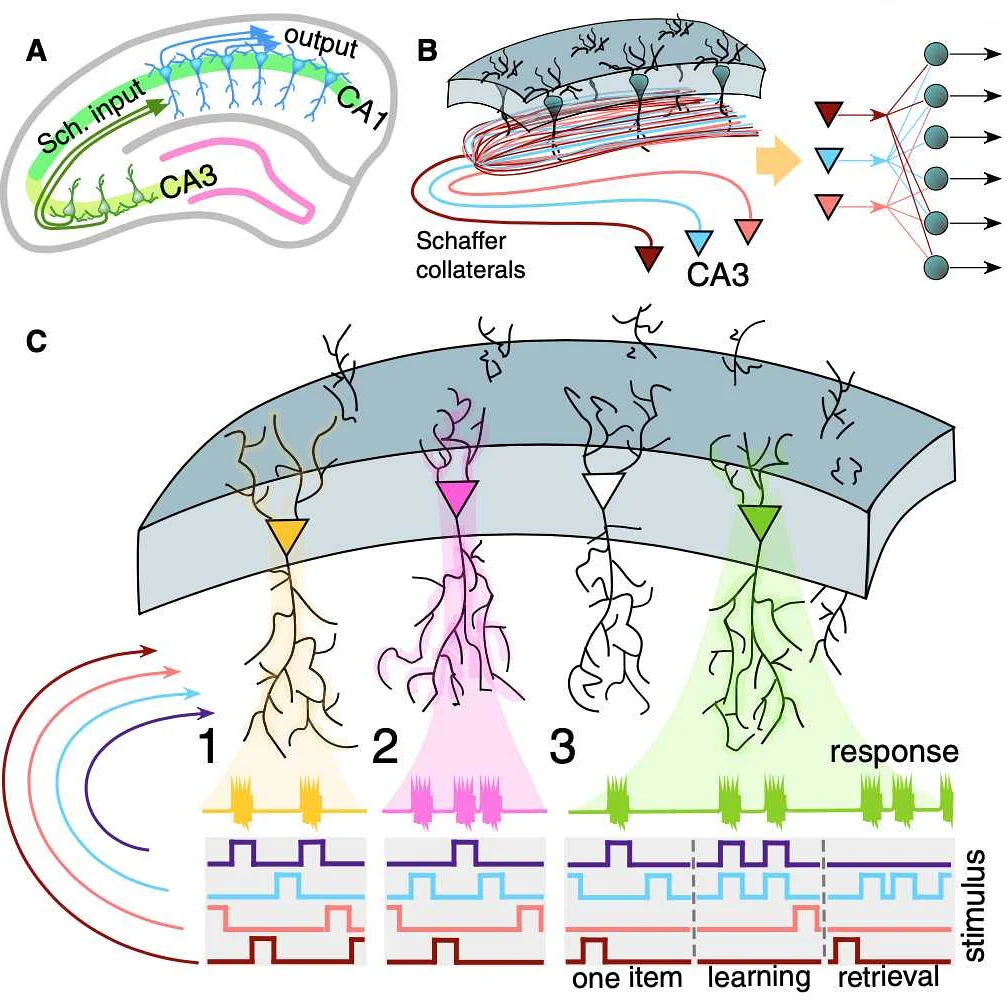
Абстрактные объекты в математике могут быть понятиями, такими как числа, функции, отношения или геометрические фигуры, которые не имеют прямого аналога в реальном мире. Они являются результатом абстракции — процесса, при котором отделяются общие свойства и характеристики объектов от их конкретных вариаций и проявлений. Абстрактные объекты представлены символами, формулами и определениями, которые позволяют работать с ними и проводить различные операции и доказательства.
Абстрактность в математике играет важную роль, поскольку позволяет упрощать и обобщать сложные и конкретные понятия, создавая формальные системы и теории, которые могут быть применены в различных областях знаний. Она позволяет математикам работать с абстрактными объектами и решать сложные задачи, используя логические рассуждения, доказательства и математические методы. Таким образом, абстрактность в математике является ключевым элементом для развития и прогресса этой науки.
Примеры абстрактных концепций в математике:
— Комплексные числа: комплексные числа — это абстрактное расширение обычных вещественных чисел, которое включает в себя мнимую единицу. Они используются, например, в электрических и электронных инженерных расчетах.
— Векторы: векторы — это абстрактные математические объекты, которые имеют направление и величину. Они используются в физике, геометрии, механике и других науках для описания и анализа движения и сил.
— Матрицы: матрицы — это абстрактные структуры, представляющие собой прямоугольные таблицы чисел. Они используются в линейной алгебре, теории вероятностей, компьютерной графике и других областях для представления и решения систем уравнений и преобразований.
Абстрактность в математике позволяет ученым и исследователям создавать формализованные системы и модели, которые могут быть использованы для анализа и понимания сложных явлений и процессов в различных областях знания. Она является одним из фундаментальных принципов математики и важным инструментом для развития научного мышления и исследования.
Примеры абстрактных концепций в математике
- Множество: в математике множество представляет собой абстрактный объект, который состоит из элементов без учета их порядка и повторений. Множества используются для описания и классификации различных объектов и явлений в математике.
- Функция: функция является абстрактным понятием, которое описывает зависимость между двумя множествами. Функция принимает значения из одного множества (область определения) и сопоставляет им значения из другого множества (область значений).
- Группа: группа представляет собой абстрактную структуру, которая состоит из множества элементов и операции, определенной на этом множестве. Группы используются для описания и изучения различных алгебраических структур и их свойств.
- Топология: топология является абстрактной областью математики, которая изучает свойства пространств и отношения между ними. Топология используется для описания и анализа различных геометрических объектов и их свойств.
- Алгоритм: алгоритм представляет собой абстрактное понятие, которое описывает последовательность шагов или операций, выполняемых для решения конкретной задачи. Алгоритмы используются для решения различных математических и вычислительных задач.
Это лишь некоторые из множества абстрактных концепций, которые применяются в математике. Каждая из этих концепций позволяет абстрагироваться от конкретных объектов и рассматривать их общие свойства и отношения, что является основой для дальнейшего развития математики и применения ее в различных областях науки и техники.
Взаимосвязь абстрактности с другими математическими понятиями

Абстрактность в математике тесно связана с другими понятиями и концепциями. Вот несколько примеров:
- Аксиомы и определения: Абстрактность в математике проявляется через аксиомы и определения. Аксиомы являются базовыми истинами, на которых строится математическая теория. Определения задают понятия и объекты, с которыми работает математика. Оба эти элемента являются абстрактными, так как они отделяются от конкретных явлений и фокусируются на общих свойствах и отношениях.
- Теоремы и доказательства: Абстрактность также проявляется в теоремах и доказательствах. Теоремы являются формальными утверждениями, которые могут быть доказаны с использованием логических рассуждений и ранее установленных фактов. Доказательства представляют собой логические цепочки рассуждений, которые подтверждают или опровергают данную теорему. Оба эти элемента математики абстрактны, так как они оперируют с абстрактными понятиями и символами.
- Математические структуры: Абстрактность также связана с математическими структурами, такими как группы, кольца, поля и т.д. Эти структуры определены абстрактными свойствами и операциями, которые должны быть выполнены для их классификации. Например, группа определяется набором аксиом, которые должны выполняться, чтобы объект мог быть назван группой. Математические структуры позволяют абстрактно рассматривать различные объекты и находить общие закономерности между ними.
- Абстрактные пространства: Абстрактность также проявляется в абстрактных пространствах, таких как векторные пространства, метрические пространства и функциональные пространства. Эти пространства определяются абстрактными свойствами и аксиомами, которые должны быть выполнены для их классификации. Абстрактные пространства позволяют обобщить и абстрагировать конкретные примеры и рассмотреть их в более общем контексте.
Таким образом, абстрактность в математике тесно связана с другими математическими понятиями и концепциями, и помогает нам обобщать и абстрагировать различные явления и объекты для изучения и понимания их общих свойств и закономерностей.
Роль абстрактности в развитии математической мысли
Абстрактность играет важную роль в развитии математической мысли. Она позволяет математикам обращаться с проблемами и концепциями на более общем уровне, выделяя основные идеи и законы, которые могут быть применены в различных ситуациях.
Абстрактные понятия и структуры предоставляют математикам мощный инструментарий для решения разнообразных задач и создания новых математических теорий. Например, абстрактные алгебраические структуры, такие как группы, кольца и поля, позволяют описывать и изучать общие законы и свойства чисел и операций над ними, не привязываясь к конкретным числам или операциям.
Абстракция также помогает в разработке формальных доказательств и построении строгих математических моделей. Она позволяет устранить излишние детали и фокусироваться на существенных аспектах проблемы. Благодаря этому, математики могут обобщать результаты и применять их к различным областям знания.
Кроме того, абстрактность способствует развитию математической интуиции и творческого мышления. Она позволяет видеть глубинные связи между различными концепциями и находить новые способы решения проблем. Математики часто используют абстрактные модели и идеи для создания новых математических теорий и подходов, которые впоследствии могут оказаться полезными в других областях науки и техники.
| Примеры абстрактных концепций в математике: |
| • Множества и отношения |
| • Логические операции и символы |
| • Топология и геометрические пространства |
| • Алгебраические структуры (группы, кольца, поля) |
| • Матрицы и векторы |
| • Функции и операции |
Применение абстрактности в реальных задачах и науке

Применение абстрактности в реальных задачах позволяет нам обобщать и выявлять общие закономерности, которые могут быть применимы во многих различных контекстах. Например, в физике абстрактные математические модели позволяют нам предсказывать поведение физических систем, их взаимодействие и эволюцию во времени. Без абстрактных концепций, физика была бы гораздо менее развитой и неспособной создавать новые теории и предсказывать результаты экспериментов.
Абстрактность также играет важную роль в компьютерных науках. Здесь абстрактные структуры данных и алгоритмы позволяют нам эффективно организовывать и обрабатывать большие объемы информации. Например, абстрактные структуры данных, такие как списки, деревья и графы, используются для представления информации и решения различных задач, таких как сортировка, поиск и управление ресурсами.
Абстракция также находит применение в экономике и социальных науках. Абстрактные модели позволяют нам изучать экономику и социальные системы, анализировать их поведение и предсказывать их развитие. Абстрактные концепции, такие как спрос, предложение, равновесие и оптимальность, позволяют нам анализировать сложные экономические и социальные явления и принимать обоснованные решения на основе этого анализа.
Таким образом, абстрактность играет важную роль в реальных задачах и науке, позволяя нам описывать, анализировать и предсказывать сложные явления и связи между ними. Она помогает нам обобщать и выявлять общие закономерности, что является фундаментальным для развития научного знания и решения реальных проблем.
Критика и противоречия в использовании абстрактных концепций
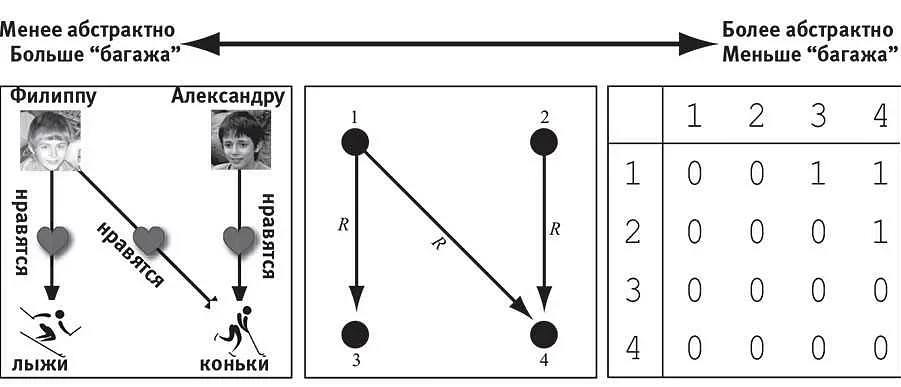
Другим аспектом критики абстрактных концепций является их недостаточная конкретность. Абстрактные понятия и определения в математике обычно являются обобщенными и несопоставимыми с конкретными объектами или явлениями. Это может вызывать затруднения при попытках применить абстрактные концепции к решению практических задач.
Также, использование абстрактных концепций в математике может приводить к противоречиям и парадоксам. Например, в теории множеств возникают парадоксы, такие как парадокс Рассела или парадокс Берри. Эти парадоксы могут подвергать сомнению саму консистентность математических систем и вызывать дискуссии в научном сообществе.
Тем не менее, несмотря на критику и противоречия, абстрактные концепции являются неотъемлемой частью математики и играют важную роль в развитии науки. Они позволяют обобщать знания, создавать новые теории и методы, а также решать сложные задачи. Без использования абстрактных концепций математика не смогла бы достичь своих современных достижений и приложений в различных областях науки и техники.
Вопрос-ответ:
Как можно определить понятие абстрактности в математике?
Абстрактность в математике означает способность выделить общие характеристики из конкретных объектов или явлений и строить на их основе общие понятия, принципы и теории. Это позволяет упростить и обобщить знания, а также создавать новые математические структуры и модели.
Какие основные концепции связаны с абстрактностью в математике?
Основные концепции, связанные с абстрактностью в математике, включают общность, формализацию, абстрактные структуры, моделирование и обратное доказательство. Общность подразумевает выделение общих свойств и отношений из множества конкретных объектов. Формализация представляет собой процесс математического описания абстрактных объектов и отношений с помощью формальных символов и правил. Абстрактные структуры включают в себя группы, кольца, поля и другие математические объекты, у которых определены операции и аксиомы. Моделирование позволяет использовать абстрактные концепции для описания и понимания реальных явлений. Обратное доказательство представляет собой метод, при котором сначала формулируется утверждение, а затем доказывается его истинность на основе абстрактных математических концепций и логических рассуждений.
Какие примеры абстрактности можно привести в математике?
В математике существует множество примеров абстрактных концепций. Например, группы являются абстрактными структурами, которые описывают свойства и операции над множествами. Матрицы и векторы также являются абстрактными объектами, которые обобщают понятия чисел и операций над ними. Понятие функции является абстрактным, так как оно описывает зависимость одной величины от другой. Теория множеств, дифференциальные уравнения, топология и другие разделы математики также полны абстрактных концепций.
Что такое абстрактность в математике?
Абстрактность в математике — это концепция, позволяющая создавать общие модели и теории, которые могут применяться к различным конкретным ситуациям. Она позволяет упростить сложные понятия и явления, выделить их основные свойства и применять их на более широком спектре проблем. Абстрактность позволяет математикам создавать абстрактные объекты, такие как числа, функции, графы и т. д., и изучать их свойства независимо от конкретных предметов или явлений.
Какие основные концепции связаны с абстрактностью в математике?
Основными концепциями, связанными с абстрактностью в математике, являются абстрактные объекты, абстрактные структуры и абстрактные системы. Абстрактные объекты — это объекты, которые представляют некоторые общие свойства и характеристики, не зависимо от конкретной реализации или предмета. Абстрактные структуры — это наборы взаимосвязанных абстрактных объектов, на которых определены некоторые операции и свойства. Абстрактные системы — это совокупности абстрактных структур, которые могут быть связаны определенными отношениями и правилами.
Можете привести примеры абстрактных концепций в математике?
Конечные и бесконечные множества — это пример абстрактной концепции в математике. Мы можем рассматривать различные множества, такие как множество всех натуральных чисел, множество всех целых чисел или множество всех действительных чисел, не обращая внимание на конкретные элементы этих множеств. Мы можем изучать их свойства, операции и отношения, независимо от конкретных чисел. Другой пример — функции. Мы можем определять функции, которые сопоставляют каждому элементу из одного множества элемент из другого множества, не уточняя конкретные значения. Мы можем изучать их свойства, графики и применять их на разных множествах.
Различия в понимании абстрактности в разных математических школах и направлениях

Понятие абстрактности в математике может различаться в разных математических школах и направлениях и зависит от контекста и целей исследования.
В классической математике абстрактность обычно связана с понятием общности. Здесь абстрактные объекты рассматриваются как представления классов или множеств, которые объединяют конкретные объекты, обладающие определенными общими свойствами. Например, множество всех натуральных чисел можно рассматривать как абстрактное понятие, объединяющее все конкретные натуральные числа.
В алгебре абстрактность связана с рассмотрением абстрактных структур и операций над ними. Например, группа — это абстрактная алгебраическая структура, в которой определены операции умножения и обратного элемента, удовлетворяющие определенным аксиомам.
В теории множеств абстрактность может быть связана с рассмотрением абстрактных множеств и операций над ними. Например, теория множеств позволяет рассматривать абстрактные конструкции, такие как бесконечные множества или множества мощности континуума.
В теории категорий абстрактность связана с рассмотрением абстрактных категорий и их морфизмов. Категория — это абстрактная математическая структура, которая позволяет рассматривать отношения и связи между различными математическими объектами.
Различия в понимании абстрактности между разными математическими школами и направлениями могут быть связаны с разными акцентами, целями и методами исследования. Однако, несмотря на различия, абстрактность является одним из фундаментальных понятий в математике и играет важную роль в развитии и применении математических теорий и методов.
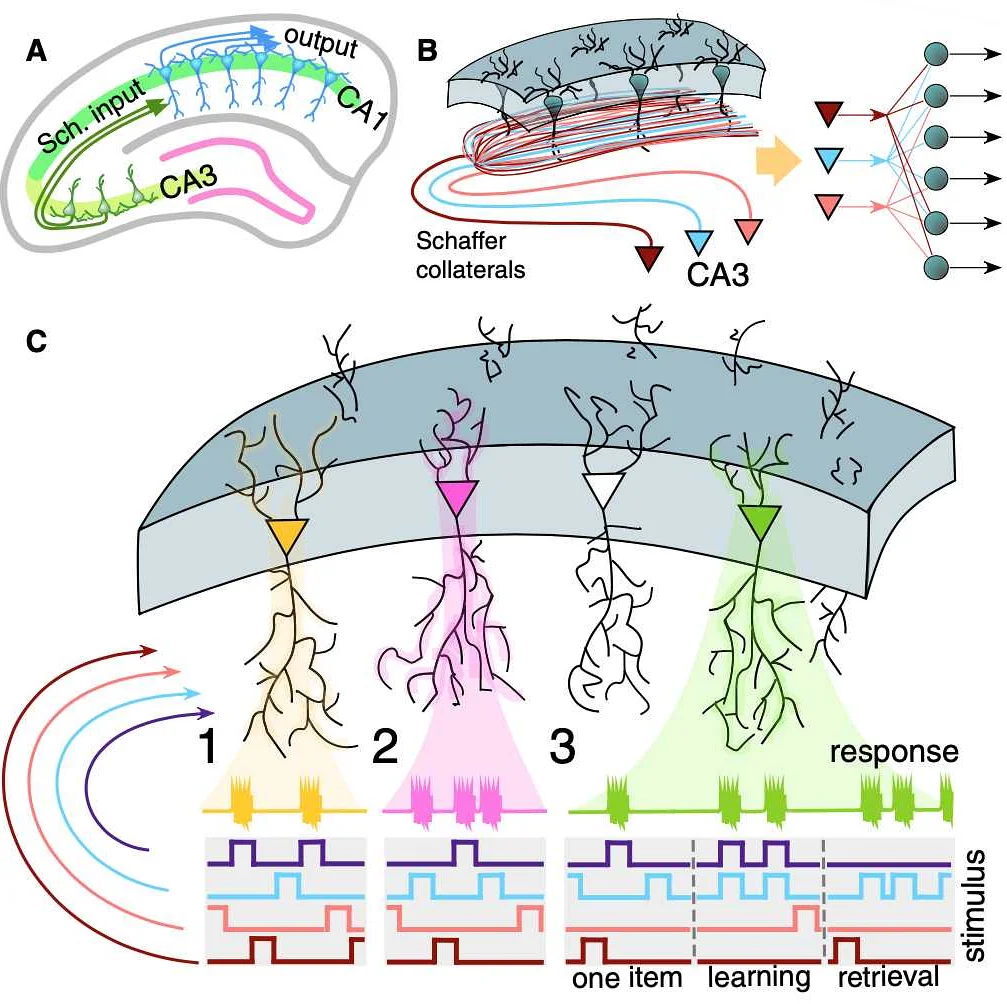

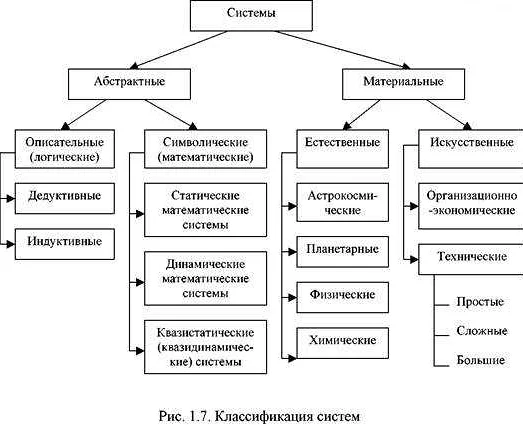

Очень интересная статья! Я всегда задавалась вопросом, что такое абстрактность в математике и как она применяется. Чтение этой статьи помогло мне разобраться в основных концепциях и примерах. Абстрактность — это способность математических объектов и понятий быть независимыми от конкретных физических или геометрических объектов. Это позволяет математикам рассматривать общие свойства и законы, которые могут быть применены в различных областях. Например, понятие функции может быть применимо как в экономике, так и в физике. Интересно, что абстрактные объекты могут быть представлены не только числами, но и графами, множествами и другими символами. Благодаря абстрактности математика имеет широкий спектр применений в реальном мире. Эта статья очень понятно объясняет сложные концепции и приводит интересные примеры. Теперь я лучше понимаю, как математика может быть абстрактной и как это связано с решением реальных проблем. Спасибо за такую информативную статью!