Что такое четная функция в математике

Четная функция в математике — это функция, которая симметрична относительно оси ординат. Значения функции для аргументов симметричных относительно нуля равны. В данной статье рассмотрим определение и свойства четных функций, а также приведем примеры их графиков.

В математике существует множество функций, которые имеют свои специфические свойства и особенности. Одной из таких функций является четная функция. Четность функции — это специальное свойство, которое характеризует ее график и определяет четность значений функции для различных аргументов.

Определение четной функции — это функция, которая обладает свойством симметрии относительно оси ординат. Другими словами, если для некоторого значения аргумента x функция f(x) равна y, то для значения аргумента -x она будет равна -y. Это означает, что график четной функции симметричен относительно оси ординат.

Четные функции обладают рядом важных свойств, которые делают их полезными для решения различных математических задач. Например, если функция f(x) является четной, то интеграл от функции f(x) на интервале [-a, a] будет равен нулю. Это свойство позволяет значительно упростить вычисления и сделать решение задачи более эффективным.

Примером четной функции может служить функция f(x) = x^2. Для любого значения аргумента x, f(x) будет равно x^2. Если же рассмотреть значение аргумента -x, то f(-x) будет равно (-x)^2, что также равно x^2. Таким образом, функция f(x) = x^2 является четной.

Определение четной функции

f(x) = f(-x)

То есть, значение функции при аргументе x равно значению функции при аргументе -x. График четной функции симметричен относительно оси ординат.

Четные функции являются важной концепцией в математике и широко применяются в различных областях, таких как алгебра, анализ и физика. Некоторые примеры четных функций включают косинус, экспоненту и параболу.

Что такое четная функция

f(x) = f(-x) для любого x в области определения функции.

Иными словами, значение функции при аргументе x равно значению функции при аргументе -x. Это означает, что график четной функции симметричен относительно оси ординат.

Примеры четных функций включают функцию y = x^2, y = |x| и y = cos(x). Все эти функции удовлетворяют условию f(x) = f(-x) и обладают симметрией относительно оси ординат.

Свойства четных функций обеспечивают некоторые удобства при их анализе и использовании. Например, если задана четная функция f(x), то значение функции в точке x можно вычислить, зная значение функции в точке -x. Это свойство симметрии позволяет сократить объем вычислений и упростить алгебраические преобразования.

Свойства четной функции

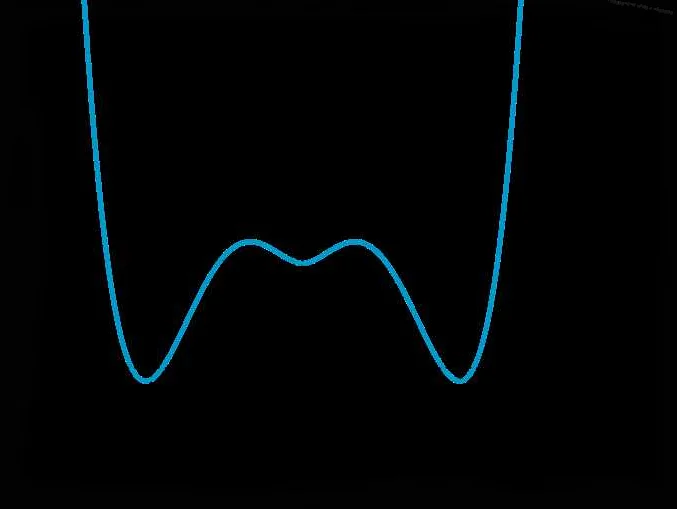
1. Значение функции симметрично относительно оси ординат. Это означает, что если (x, y) является точкой графика функции, то точка (-x, y) также будет находиться на графике.
2. Функция сохраняет свойство четности при операциях сложения и вычитания. Если f(x) — четная функция, то f(x) + f(-x) и f(x) — f(-x) также будут четными функциями.
3. Если функция f(x) — четная функция, то для любого числа a f(a) = f(-a). Это свойство позволяет найти значения функции для положительных и отрицательных аргументов.
4. График четной функции симметричен относительно оси ординат (y-оси). Это означает, что при отражении графика относительно оси ординат мы получим исходный график.
5. Четная функция может быть раскрыта в ряд Тейлора, содержащий только четные степени x. Это свойство позволяет приближенно вычислить значение функции в окрестности нуля.

Примером четной функции является функция f(x) = x^2. Ее график симметричен относительно оси ординат, и для любого числа a f(a) = f(-a).

Симметрия относительно оси OY

График четной функции симметричен относительно оси OY, что означает, что если точка (x, f(x)) принадлежит графику функции, то точка (-x, f(-x)) также принадлежит графику. Другими словами, если отразить график функции относительно оси OY, то получим исходный график.

Примером четной функции является функция f(x) = x2. Для любого значения x выполняется условие f(x) = f(-x). Например, при x = 2 мы имеем f(2) = 22 = 4, а при x = -2 также получаем f(-2) = (-2)2 = 4.

Четность всех степеней

Для доказательства этого свойства можно воспользоваться определением четности функции. По определению, функция f(x) является четной, если для любого x выполняется условие f(-x) = f(x). То есть, значение функции для отрицательного аргумента равно значению функции для соответствующего положительного аргумента.

Пусть f(x) — четная функция. Тогда для любого целого числа n выполняется:

f((-x)n) = f((-1)n * xn) = f((-1)n) * f(xn)

Так как (-1)n равно 1 при четном n и -1 при нечетном n, получаем:

f((-x)n) = f(xn)

Таким образом, четная функция сохраняет четность всех степеней, что является еще одним важным свойством таких функций.

Примеры четных функций

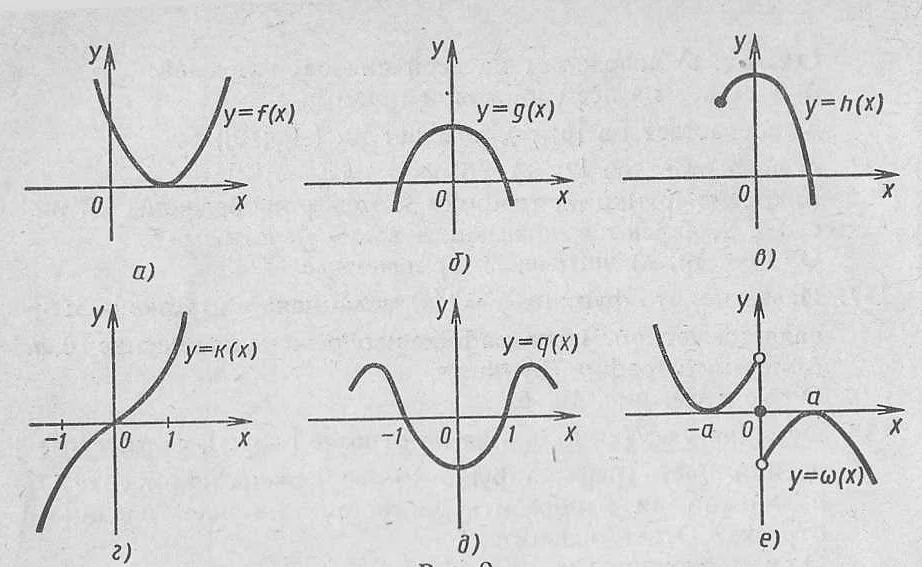
Приведем некоторые примеры четных функций:

ФункцияОпределение

Квадратичная функция	f(x) = x2
Косинус	f(x) = cos(x)
Арккосинус	f(x) = arccos(x)
Модуль	f(x) = |x|

Это лишь некоторые примеры из множества четных функций. Важно знать, что если функция f(x) является четной, то для любого значения x функция f(x) будет равна f(-x).

Квадратная функция

Основными свойствами квадратной функции являются:

1. График квадратной функции представляет собой параболу в форме «U». Вершина параболы находится в точке (-b/2a, f(-b/2a)).
2. Если a > 0, то парабола открывается вверх, и функция имеет минимум. Если a < 0, то парабола открывается вниз, и функция имеет максимум.
3. Если a = 0, то функция становится линейной, и график представляет собой прямую линию.
4. Корни квадратного уравнения ax^2 + bx + c = 0 можно найти с помощью формулы дискриминанта: x = (-b ± √(b^2 — 4ac))/(2a).
5. Квадратная функция может принимать как положительные, так и отрицательные значения в зависимости от значений a, b и c.

Примеры квадратных функций:

• f(x) = x^2 — функция, график которой открывается вверх, вершина параболы находится в точке (0, 0).
• f(x) = -2x^2 + 3x + 1 — функция, график которой открывается вниз, вершина параболы находится в точке (3/4, 7/8).
• f(x) = 4x^2 — 8x + 3 — функция, график которой открывается вверх, вершина параболы находится в точке (1, -1).

Косинусная функция

Косинусная функция определена для всех действительных чисел и имеет период 2π. Ее график представляет собой колебания между значениями -1 и 1 на оси ординат в зависимости от значения аргумента на оси абсцисс.

Основные свойства косинусной функции:

1. Косинусная функция является четной функцией, то есть cos(x) = cos(-x) для любого x.
2. Максимальное значение косинусной функции равно 1, достигается при аргументе, равном 0.
3. Минимальное значение косинусной функции равно -1, достигается при аргументе, равном π или -π.
4. Косинусная функция является периодической с периодом 2π, то есть cos(x + 2π) = cos(x) для любого x.

Примеры применения косинусной функции:

• В геометрии косинус используется для решения треугольников и нахождения длин сторон и углов.
• В физике косинусная функция используется для описания колебаний и волн, например, в гармоническом движении.
• В математическом анализе косинусная функция используется для нахождения производной и интеграла от других функций.

Применение четных функций

Четные функции находят широкое применение в математике и других науках. Их свойства позволяют упростить многие расчеты и анализы.

Одно из важных применений четных функций — нахождение симметричных точек на графике. Поскольку четная функция симметрична относительно оси ординат, можно сразу знать значение функции в точке (x, y) по значению в точке (-x, y). Это позволяет существенно сократить количество вычислений и упростить анализ графика.

Кроме того, четные функции часто используются для моделирования симметричных явлений. Например, в физике часто возникают физические процессы, которые проявляются симметрично относительно некоторой оси, и для их описания и анализа используются именно четные функции.

Еще одно применение четных функций связано с интегралами. Если функция является четной, то ее определенный интеграл на симметричном отрезке [-a, a] равен удвоенному интегралу на положительном отрезке [0, a]. Это свойство может быть использовано для упрощения вычислений.

Таким образом, четные функции играют важную роль в математике и науках, позволяя упростить анализ, моделирование и вычисления симметричных явлений.

Симметрия графиков

Симметрия графиков четных функций проявляется в том, что симметричные относительно оси ординат точки имеют одинаковые ординаты. Другими словами, если для некоторого значения аргумента функции f(x) равно у, то для значения аргумента -а функция принимает такое же значение y.

Например, рассмотрим функцию f(x) = x^2. Ее график является четным и симметричен относительно оси ординат. Если для аргумента x = 2 значение функции равно y = 4, то для аргумента x = -2 значение функции также будет равно y = 4. График функции представляет собой параболу, которая отражается от оси ординат.

Симметрия графиков четных функций является важным свойством, которое позволяет упростить анализ и построение графиков таких функций. Она позволяет сделать выводы о поведении функции в одной части графика, на основании данных из другой симметричной части.

Видео по теме:

Что такое четная функция в математике?

Четная функция в математике — это функция, которая обладает свойством симметрии относительно оси ординат. То есть, если для некоторого значения x функция f(x) определена, то значение f(-x) также определено и равно f(x).

Как можно определить, является ли функция четной?

Чтобы определить, является ли функция четной, необходимо проверить выполнение условия симметрии относительно оси ординат. Для этого достаточно проверить, что f(-x) = f(x) для всех значения x, для которых функция определена.

Какую пользу можно извлечь из изучения четных функций?

Изучение четных функций имеет немало применений. Например, знание того, что функция является четной, может помочь в упрощении выражений и решении уравнений. Также, свойства четных функций широко используются в физике и инженерии для моделирования и анализа различных процессов.

Что такое четная функция?

Четная функция — это функция, значение которой для аргумента x равно значению функции для аргумента -x. Другими словами, она обладает симметрией относительно оси OY.