Симметрия в математике 3 класс что такое
Содержимое
- 1 Симметрия в математике 3 класс что такое
- 1.1 Изучаем симметрию в математике для 3 класса
- 1.2 Видео по теме:
- 1.3 Что такое симметрия?
- 1.4 Как определить симметричную фигуру?
- 1.5 Вопрос-ответ:
- 1.6 Какие виды симметрии существуют?
- 1.7 Как использовать зеркальную симметрию в задачах?
- 1.8 Почему симметрия важна в математике?
- 1.9 Какие другие области науки используют понятие симметрии?
- 1.10 Как развивать навыки работы с симметрией?
- 1.11 Задачи и упражнения по симметрии для третьего класса
Симметрия в математике для учеников 3 класса: что это такое и как она применяется в учебе. Узнайте об основных понятиях симметрии и методах ее изучения, чтобы развить логическое мышление и умение решать задачи.
В мире математики симметрия – это одно из самых интересных и захватывающих понятий. Она встречается повсюду – в природе, искусстве, архитектуре и, конечно же, в математике. Симметрия – это свойство объекта или фигуры сохранять свою форму или структуру при определенных преобразованиях. В этой статье мы рассмотрим, что такое симметрия и как ее понять для учеников 3 класса.
Основные типы симметрии – это осевая и плоскостная симметрии. Осевая симметрия – это свойство фигуры иметь ось, относительно которой она симметрична. Это значит, что при отражении фигуры относительно этой оси она сохраняет свою форму. Например, буква «А» имеет осевую симметрию – ее верхняя часть симметрична нижней. Плоскостная симметрия – это свойство фигуры быть симметричной относительно плоскости. Например, круг является фигурой с плоскостной симметрией – любая его часть сохраняет свою форму при отражении относительно плоскости.
Математика не только помогает нам понять мир вокруг нас, но и развивает логическое мышление, воображение и способность анализировать. Изучение симметрии позволяет детям визуально воспринимать и анализировать фигуры, развивает их внимание и умение находить решения задач. Более того, понятие симметрии имеет практическое применение в жизни – благодаря нему создаются красивые и гармоничные изделия и постройки.
Понимание симметрии может быть сложным для учеников 3 класса, поэтому важно использовать подходящие методы и примеры, чтобы помочь им осознать это понятие. Рекомендуется начать с простых упражнений, где дети будут отражать изображения относительно оси или плоскости, размещать фигуры таким образом, чтобы создавалась симметричная композиция, и отмечать симметричные элементы в различных объектах. Это позволит им на практике прочувствовать и увидеть, что такое симметрия, и как она проявляется в реальном мире.
Изучаем симметрию в математике для 3 класса
В третьем классе дети начинают изучать симметрию и узнают о различных видам симметрии. Главное, что нужно понять, это то, что симметричные фигуры могут быть одинаковыми, если их развернуть или отразить.
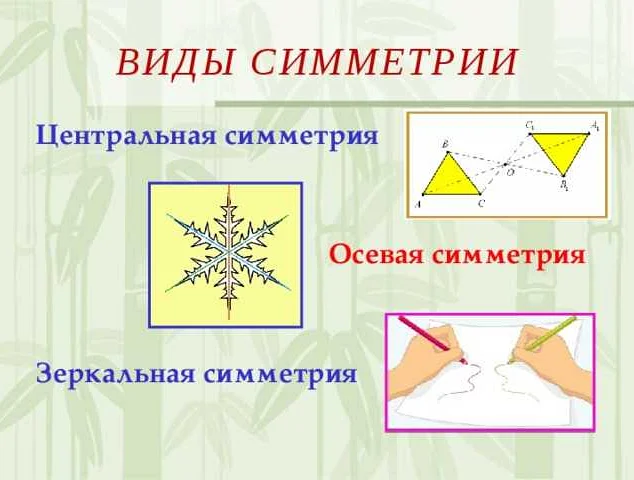
Симметрия бывает осевой и центральной. Осевая симметрия имеет ось отражения, которая делит фигуру на две равные части. Центральная симметрия имеет точку отражения, относительно которой фигура симметрична.
Важно научить детей различать симметричные и несимметричные фигуры. Для этого можно использовать зеркало и проверять, может ли фигура быть отражена в нем так, чтобы получить исходную фигуру.
Изучение симметрии помогает детям развивать логическое мышление, улучшает пространственное восприятие и способствует развитию художественных навыков. Дети могут создавать свои собственные симметричные рисунки и фигуры, что развивает их творческий потенциал.
Запомните:
- Симметрия — это равенство частей относительно оси или точки.
- Симметрия бывает осевой и центральной.
- Изучение симметрии развивает логическое мышление и художественные навыки.
Исследуйте и изучайте симметрию вместе с детьми, чтобы они могли лучше понять мир форм и изображений!
Видео по теме:
Что такое симметрия?
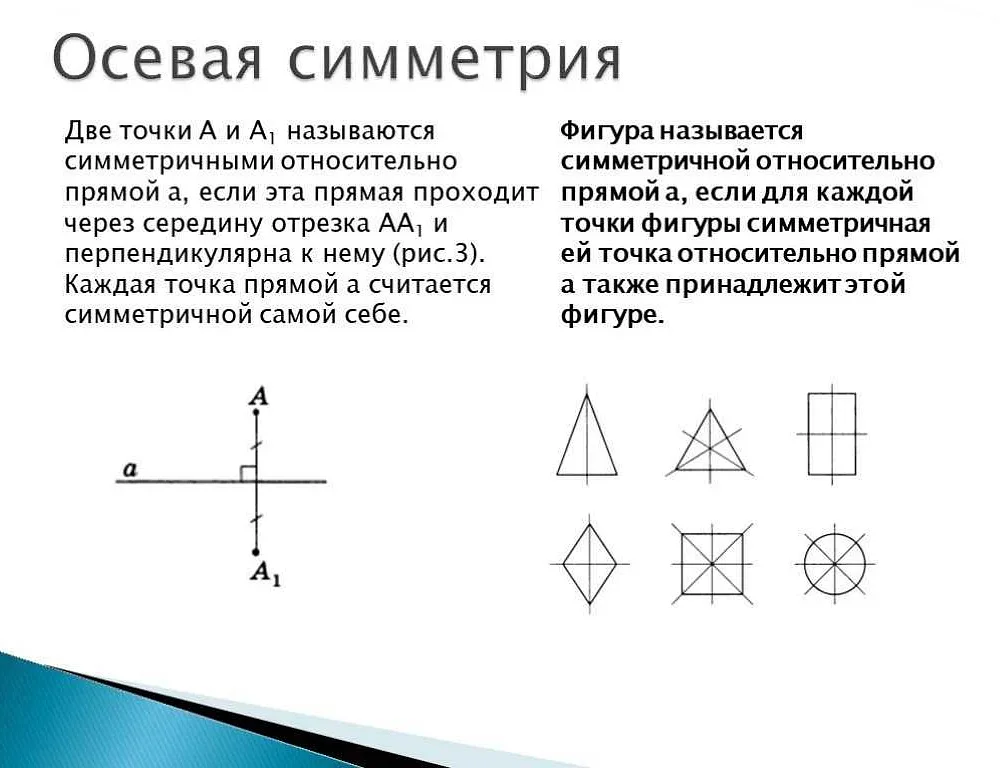
В математике выделяют несколько видов симметрии:
Вид симметрииОписание
| Осевая симметрия | Объекты, которые имеют осевую симметрию, могут быть разделены на две равные части путем отражения относительно оси. |
| Центральная симметрия | Объекты, которые имеют центральную симметрию, могут быть разделены на две равные части путем отражения относительно центральной точки. |
| Поворотная симметрия | Объекты, которые имеют поворотную симметрию, могут быть повернуты на определенный угол вокруг некоторой точки, чтобы совместиться с самими собой. |
Симметрия широко используется в геометрии, искусстве, архитектуре и других областях. Понимание симметрии помогает нам анализировать и создавать изображения, находить закономерности и решать задачи.
Как определить симметричную фигуру?
Чтобы определить, является ли фигура симметричной, можно использовать несколько способов:
- Использование зеркальной оси: можно провести воображаемую линию, такую как зеркало, через фигуру. Если обе части фигуры выглядят одинаково, то фигура симметрична по отношению к этой оси.
- Сверление фигуры: можно сверить фигуру на прозрачной бумаге и сложить ее с самой собой. Если фигура полностью совпадает, то она симметрична.
- Использование симметричных поворотов: можно повернуть фигуру на 180 градусов вокруг центра и проверить, совпадают ли она с исходной фигурой. Если да, то фигура симметрична.
Изучение симметрии помогает развивать визуальное восприятие и логическое мышление у детей. Они могут использовать эту концепцию для решения задач в геометрии и других областях математики.
Вопрос-ответ:
Что такое симметрия?
Симметрия — это особое свойство геометрических фигур, при котором они могут разделяться на две половины, которые являются зеркальными отражениями друг друга. То есть, если мы проведем прямую линию (ось симметрии) через фигуру, то каждая половина будет симметрична другой относительно этой оси.
Как понять, что фигура симметрична?
Для того чтобы понять, что фигура симметрична, нужно провести ось симметрии через нее. Если обе половины фигуры выглядят одинаково, как в зеркале, то фигура симметрична.
Какие бывают виды симметрии?
В математике существует несколько видов симметрии. Одним из наиболее распространенных видов является осевая симметрия, когда фигура делится на две симметричные относительно оси части. Также есть центральная симметрия, когда фигура симметрична относительно центральной точки.
Где используется симметрия в жизни?
Симметрия используется в различных областях нашей жизни. Например, в архитектуре, где симметричные элементы фасадов зданий придают им гармоничный и красивый вид. Также симметрия применяется в дизайне, создании узоров, в образовании и науке, в технике и многих других областях.
Как можно использовать знания о симметрии в математике в повседневной жизни?
Знание о симметрии в математике может быть полезным в повседневной жизни. Например, при создании и оценке дизайна одежды или интерьера, при решении головоломок и задач по логике, при планировании и строительстве различных объектов. Также понимание симметрии помогает улучшить визуальное восприятие и развивает логическое мышление.
Что такое симметрия?
Симметрия — это свойство фигур и объектов, которые могут быть разделены на две равные части, симметричные друг другу относительно некоторой оси.
Какие виды симметрии существуют?
В математике существует несколько видов симметрии:
| По отношению к прямой | Симметрия относительно прямой является самым простым видом симметрии. Если фигуру можно сложить пополам так, что одна ее половина станет зеркальным отражением другой половины, то эта фигура обладает симметрией относительно прямой. |
| По отношению к точке | Симметрия относительно точки означает, что фигура может быть повернута так, что каждая точка на фигуре будет совпадать с точкой, находящейся на той же расстоянии от центральной точки, но с противоположным направлением. |
| По отношению к центру | Симметрия относительно центра подразумевает, что фигура может быть повернута на 180 градусов вокруг центральной точки без изменения своей формы. |
Эти виды симметрии играют важную роль в геометрии и помогают нам лучше понять и классифицировать различные фигуры и объекты.
Как использовать зеркальную симметрию в задачах?

Одним из способов использования зеркальной симметрии в задачах является определение отсутствующих элементов фигуры. Если известна только половина фигуры, то можно использовать зеркальную симметрию для определения остальной части. Например, если известна половина симметричной фигуры, то можно отразить ее по зеркальной оси и получить полную фигуру.
Другим способом использования зеркальной симметрии является решение задач на нахождение симметричных элементов. Если известны координаты одного элемента относительно зеркальной оси, то можно использовать зеркальность для нахождения координат симметричного элемента. Например, если известны координаты точки (3, 4) относительно зеркальной оси, то симметричная точка будет иметь координаты (-3, 4).
Зеркальная симметрия также может использоваться для решения задач на определение симметричности фигур. Если фигура имеет зеркальную симметрию, то можно использовать ее свойства для определения симметричности других фигур. Например, если одна фигура имеет зеркальную симметрию относительно горизонтальной оси, то другая фигура, которая совпадает с первой после отражения, также будет иметь зеркальную симметрию.
Важно помнить, что для использования зеркальной симметрии в задачах необходимо понимание основных понятий и свойств. Зеркальная симметрия может быть применена для решения различных задач на определение формы фигур, нахождение недостающих элементов и определение симметричности. Практика и тренировка помогут лучше понять и использовать зеркальную симметрию в математических задачах.
Почему симметрия важна в математике?
Симметрия помогает нам в решении задач и построении геометрических фигур. Она позволяет нам видеть отражение и вращение объектов, а также анализировать их характеристики, такие как количество сторон и углов.
Кроме того, симметрия является одним из основных принципов визуального искусства. Понимание симметрии позволяет нам создавать гармоничные и сбалансированные композиции, которые приятно воспринимать глазу.
Таким образом, понимание и использование симметрии в математике помогает нам развивать логическое мышление, улучшать наблюдательность и креативность, а также применять математические принципы в различных областях нашей жизни.
Какие другие области науки используют понятие симметрии?
Еще одной областью, где применяется понятие симметрии, является химия. В химических соединениях симметрия молекул определяет их свойства и взаимодействия. Изучение симметрии молекул позволяет предсказывать и объяснять химические реакции и физические свойства веществ.
Биология также использует понятие симметрии при изучении организмов. Многие животные и растения обладают симметричным строением тела, что облегчает их адаптацию к окружающей среде и взаимодействие с другими организмами.
Искусство и дизайн также часто используют симметрию в своем творчестве. Симметричные формы и композиции создают гармоничный и эстетически привлекательный образ.
Таким образом, понятие симметрии применяется во множестве научных и творческих областей, помогая понять особенности объектов и явлений, а также создать гармонию и красоту.
Как развивать навыки работы с симметрией?

Одним из способов развивать навыки работы с симметрией является проведение различных упражнений и заданий, которые основаны на принципе симметрии. Например, ребенку можно предложить нарисовать половину фигуры, а затем симметрично дополнить ее, чтобы получить полную фигуру. Также можно предлагать ребенку находить симметричные элементы в различных геометрических фигурах и рисунках.
Важно обратить внимание на то, что развитие навыков работы с симметрией не только способствует развитию математических способностей, но и развивает воображение, творческое мышление, а также улучшает координацию движений.
При проведении упражнений по работе с симметрией можно использовать различные материалы, такие как цветные карандаши, фломастеры, ножницы и бумага. Кроме того, существуют также специальные задания и игры, разработанные для развития навыков работы с симметрией, которые можно использовать вместе с учебником.
Важно помнить, что развитие навыков работы с симметрией должно быть постепенным и систематичным. Поэтому, регулярная практика и повторение играют важную роль в процессе освоения этого математического понятия.
Таким образом, развитие навыков работы с симметрией является важной частью математического образования для 3 класса. Проведение упражнений и заданий, использование различных материалов и игр, а также регулярная практика позволят детям лучше понять и применять понятие симметрии.
Задачи и упражнения по симметрии для третьего класса
Задачи и упражнения по симметрии помогают детям развить визуальное восприятие, логическое мышление и творческие способности. Вот несколько задач, которые помогут третьеклассникам лучше понять симметрию:
1. Распознавание симметричных фигур:
Задача:
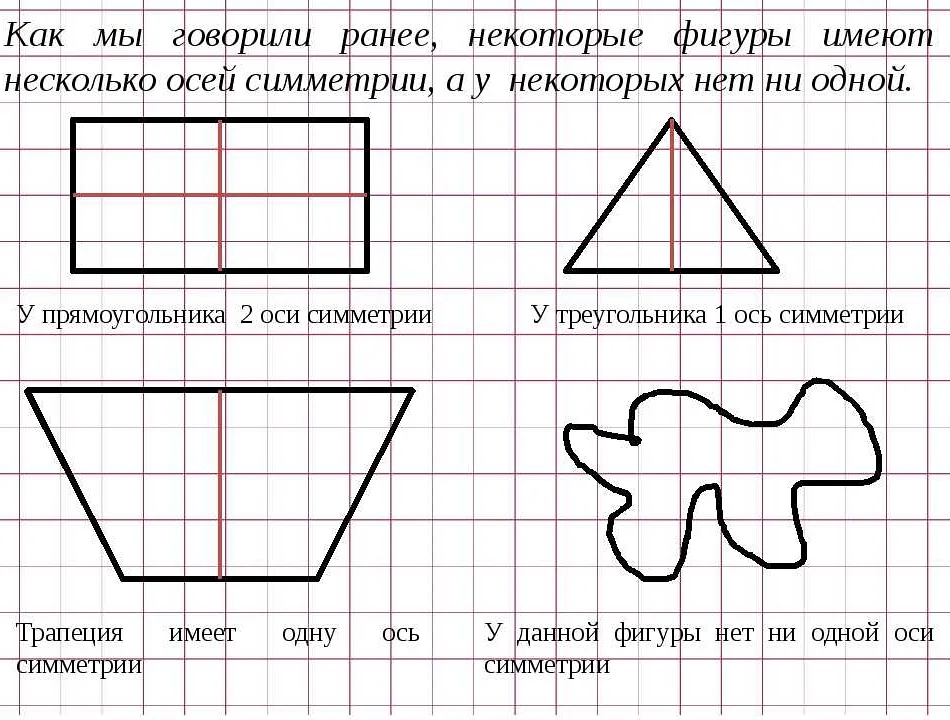
Посмотри на каждую фигуру и определи, является ли она симметричной. Если да, найди ось симметрии.

Ответ: Фигура 1 — несимметричная. Фигура 2 — симметричная, ось симметрии — вертикальная линия, проходящая посередине. Фигура 3 — симметричная, ось симметрии — горизонтальная линия, проходящая посередине.
2. Построение симметричных фигур:
Задача:
Используя линейку и цветные карандаши, нарисуй симметричную фигуру к каждой из предложенных:

Ответ: Нарисуй симметричную фигуру относительно оси симметрии. Пример: для фигуры 1, проведи вертикальную линию посередине и нарисуй зеркальное отражение справа от нее.
3. Угадай симметричную фигуру:
Задача:
Разгляди фигуру на левой стороне и выбери правильную симметричную фигуру из вариантов:

Ответ: Правильная симметричная фигура — B.
Задачи и упражнения по симметрии помогают третьеклассникам лучше понять основы геометрии и развивают их математические навыки. Они также способствуют развитию визуального восприятия и творческого мышления. Работая с симметрией, дети учатся находить равенство и гармонию в окружающем мире.
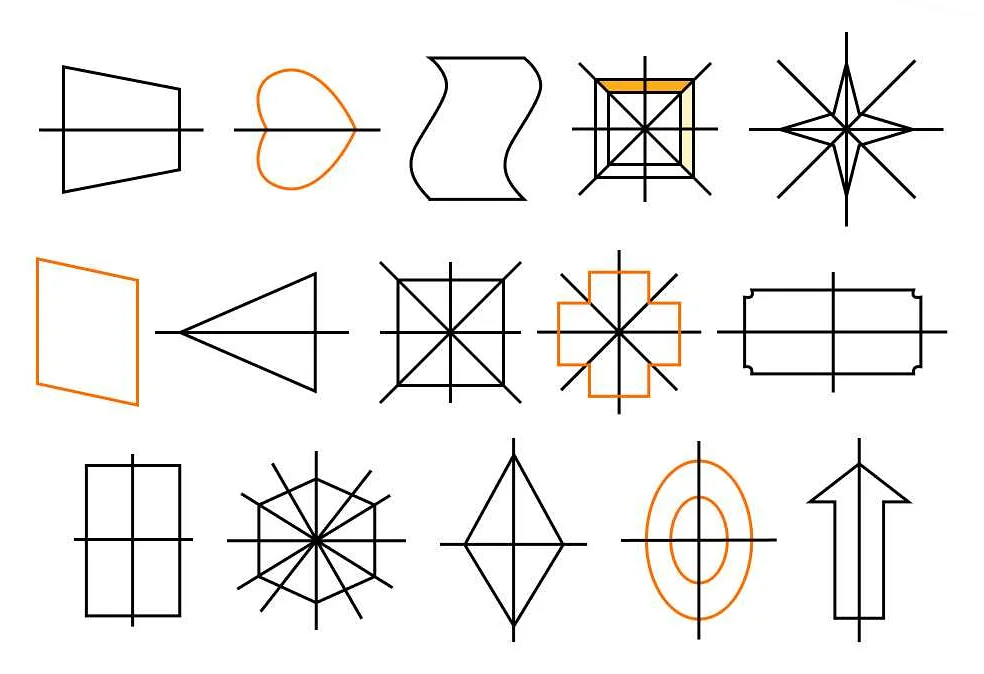
Статья очень интересная! Я узнала много нового о симметрии в математике. Теперь мне понятно, что такое ось симметрии и как ее определить. Было интересно узнать, что в природе и окружающем нас мире тоже есть много примеров симметрии. Теперь я смогу обращать внимание на симметричные фигуры и объекты вокруг меня. Статья написана понятным языком, что очень важно для детей третьего класса. Я с нетерпением жду новых статей на эту тему, чтобы продолжить изучать симметрию в математике. Спасибо автору за такую интересную и полезную информацию!