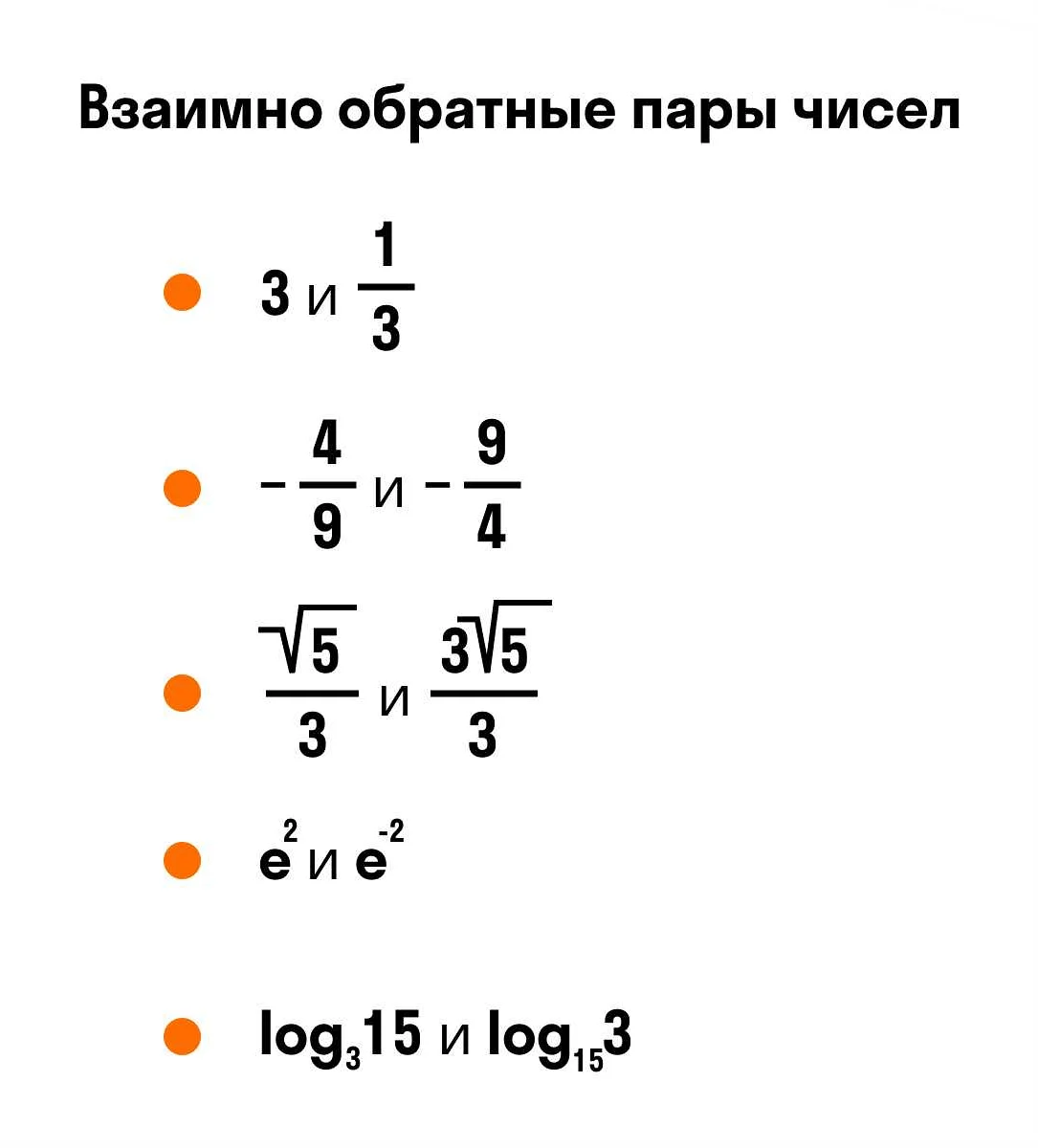
Что такое число обратное данному в математике
Содержимое
- 1 Что такое число обратное данному в математике
- 1.1 Что такое число обратное данному: определение и примеры в математике
- 1.2 Число обратное: определение и понятие
- 1.3 Обратное число: основные свойства и характеристики
- 1.4 Как найти число, обратное данному
- 1.5 Обратное число: примеры из практики
- 1.6 Обратное число и операции
- 1.7 Обратное число и дроби
- 1.8 Вопрос-ответ:
- 1.9 Обратное число и проценты
- 1.10 Видео по теме:
Обратное число в математике — это число, при умножении на которое данное число дает единицу. Обратное число можно найти путем деления единицы на данное число. Например, обратное число для числа 5 равно 1/5 или 0.2. Обратные числа играют важную роль в алгебре и арифметике, и используются при решении уравнений и выполнении других математических операций.
В математике существует понятие «обратное число», которое играет важную роль в различных операциях и вычислениях. Обратное число — это число, при умножении на которое получается единица. Например, обратным числом к 5 является 1/5, так как 5 * (1/5) = 1. Обратное число можно найти для любого числа, за исключением нуля, так как умножение на ноль не определено.
Обратные числа имеют свойства, которые помогают в вычислениях. Например, если у нас есть два числа a и b, и их произведение равно единице, то a и b являются обратными числами друг к другу. Это свойство позволяет нам находить обратные числа с помощью деления. Например, обратным числом к 3 будет 1/3, так как 3 * (1/3) = 1.
Примеры обратных чисел в математике включают обратные числа к целым числам, десятичным дробям и дробям. Обратным числом к 2 является 1/2, так как 2 * (1/2) = 1. Обратным числом к 0.5 будет 2, так как 0.5 * 2 = 1. Обратным числом к 1/4 будет 4, так как (1/4) * 4 = 1. Таким образом, обратные числа помогают нам выполнять различные операции и решать математические задачи.
Обратные числа играют важную роль в различных областях математики, таких как алгебра, геометрия, теория вероятностей и других. Они используются для решения уравнений, вычисления вероятностей, нахождения обратных функций и многих других задач. Понимание понятия обратного числа и его свойств помогает нам лучше понять и применять математические концепции и методы в решении различных задач и проблем.
Что такое число обратное данному: определение и примеры в математике

Чтобы найти число обратное данному, необходимо разделить единицу на исходное число. Формула для нахождения обратного числа выглядит следующим образом:
Обратное число = 1 / исходное число
Например, для числа 2, обратное число будет равно 1/2 или 0.5. Для числа -5, обратное число будет равно 1/(-5) или -0.2. Обратное число всегда имеет противоположный знак по сравнению с исходным числом.
Обратные числа имеют важное значение в различных областях математики и физики. Они используются, например, при решении уравнений, векторных операциях, в теории вероятности и др. Обратные числа также участвуют в определении обратных функций.
Число обратное: определение и понятие

Обратные числа существуют для всех ненулевых чисел. Например, обратным числом для числа 2 является 0.5, так как 2 * 0.5 = 1.
Обратные числа часто используются в математических операциях, таких как деление. Если нужно разделить число на другое число, то можно умножить его на обратное число. Например, чтобы разделить 8 на 4, можно умножить 8 на обратное число для 4, то есть 0.25. Таким образом, 8 / 4 = 8 * 0.25 = 2.
Обратные числа также важны в алгебре и при решении уравнений. Они позволяют нам решать уравнения с помощью умножения и деления, а не только с помощью сложения и вычитания.
Итак, обратное число — это число, которое при умножении на данное число дает единицу. Они играют важную роль в математике и позволяют нам выполнять различные операции, такие как деление и решение уравнений.
Обратное число: основные свойства и характеристики
Существует несколько свойств обратного числа:
1. Сумма числа и его обратного равна нулю:
Если данное число равно a, то сумма числа a и его обратного числа равна нулю:
a + a⁻¹ = 0
2. Произведение числа и его обратного равно единице:
Если данное число равно a, то произведение числа a и его обратного числа равно единице:
a * a⁻¹ = 1
3. Обратное число нуля не существует:
Ноль не имеет обратного числа, так как умножение нуля на любое число дает ноль, а не единицу.
Обратное число играет важную роль в решении уравнений и в математических операциях, таких как деление и вычисление обратной матрицы. Без понимания обратного числа невозможно успешно изучать алгебру и другие разделы математики.
Поэтому, знание основных свойств и характеристик обратного числа является важным для понимания и применения математических концепций и операций.
Как найти число, обратное данному

Чтобы найти число, обратное данному числу, нужно выполнить несколько простых шагов.
1. Возьмите данное число и запишите его в виде десятичной дроби с числителем 1. Например, если данное число равно 5, то запишите его как 1/5.
2. Переверните дробь, поменяв местами числитель и знаменатель. В нашем примере получим 5/1.
3. Полученная дробь является числом, обратным данному числу. В нашем примере число обратное 5 равно 5/1 или просто 5.
Таким образом, чтобы найти число, обратное данному числу, нужно записать его в виде десятичной дроби с числителем 1, перевернуть дробь и полученная дробь станет числом, обратным данному числу.
Примеры:
Число 2 обратное числу 2 равно 1/2 или 0.5.
Число 10 обратное числу 10 равно 1/10 или 0.1.
Число -3 обратное числу -3 равно 1/-3 или -1/3.
Обратное число: примеры из практики
Исходное числоОбратное число
| 2 | 0.5 |
| 5 | 0.2 |
| 0.25 | 4 |
| 10 | 0.1 |
В первом примере исходное число равно 2, а его обратное число равно 0.5. Это означает, что если умножить 2 на 0.5, то получим 1. Аналогично, для числа 5 его обратное число равно 0.2, что означает, что если умножить 5 на 0.2, то получим 1.
Во втором примере число 0.25 имеет обратное число 4. Это значит, что если умножить 0.25 на 4, то получим 1.
В третьем примере число 10 имеет обратное число 0.1. Если умножить 10 на 0.1, то получим 1.
Таким образом, обратное число является числом, умножение на которое дает результат равный 1. В приведенных примерах можно видеть, что обратное число всегда обратно пропорционально исходному числу.
Обратное число и операции
Операции с обратными числами выполняются следующим образом:
ОперацияОбратная операция
| Сложение | Вычитание |
| Вычитание | Сложение |
| Умножение | Деление |
| Деление | Умножение |
Например, обратное число к 2 равно 0.5, так как 2 * 0.5 = 1. Обратное число к -3 равно -0.3333, так как -3 * -0.3333 ≈ 1.
Обратное число и дроби
Для примера, обратное число для 2 будет 1/2, так как 2 * 1/2 = 1. Аналогично, обратное число для 3/4 будет 4/3, так как (3/4) * (4/3) = 1.
Обратные числа особенно полезны при выполнении операций деления и умножения с дробями. Например, если нужно разделить одну дробь на другую, можно просто умножить первую дробь на обратное второй дроби число.
Определение обратного числа в математике играет важную роль и используется в различных областях, таких как алгебра, геометрия и физика.
Вопрос-ответ:
Что такое число обратное данному?
Число обратное данному – это число, при умножении на которое исходное число будет равно единице.
Как найти число обратное данному числу?
Чтобы найти число обратное данному числу, нужно взять единицу и разделить ее на исходное число. Например, если дано число 5, то обратное ему число будет 1/5.
Какие свойства имеют числа обратные друг другу?
Числа, обратные друг другу, обладают следующими свойствами: их произведение равно единице, они отличаются знаком и имеют одинаковую абсолютную величину.
Может ли число обратное быть дробным?
Да, число обратное может быть дробным. Например, если дано число 2, то его обратное число будет 1/2, что является дробью.
Какие примеры чисел обратных можно привести?
Примеры чисел обратных: 2 и -2, 1/3 и -1/3, 5 и -5. Все эти числа при умножении на свои обратные дают результат равный единице.
Обратное число и проценты
Обратное число можно использовать при решении задач, связанных с процентами. Например, если нам известно, что какое-то число составляет определенный процент от другого числа, то мы можем найти это другое число, используя обратное число.
Для нахождения числа, которое составляет определенный процент от другого числа, мы делим это число на процент. Например, если мы знаем, что 25% от числа равно 50, то мы можем найти это число, разделив 50 на 25%, что равно 200.
Также, обратное число можно использовать при решении задач на находение процента от числа. Например, если нам известно, что какое-то число составляет определенный процент от другого числа, то мы можем найти этот процент, используя обратное число.
Для нахождения процента от числа, мы делим это число на само число и умножаем на 100%. Например, если мы знаем, что число 50 составляет 25% от другого числа, то мы можем найти этот процент, разделив 50 на число, и умножив на 100%, что равно 200.


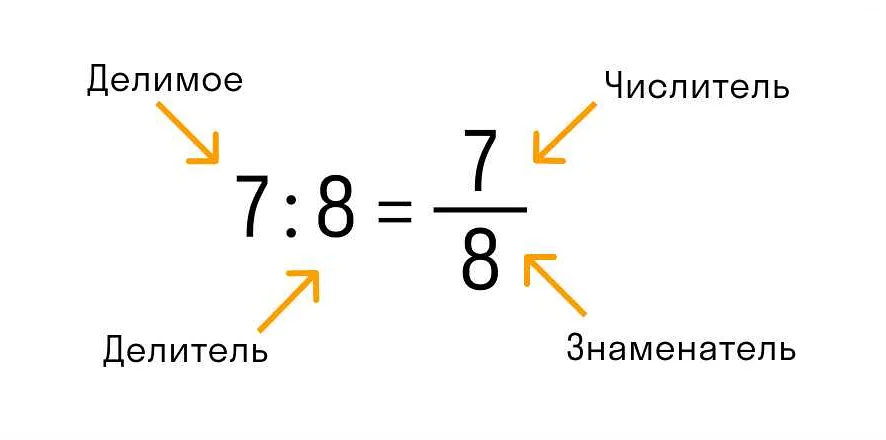
Статья очень интересная и познавательная! Благодаря ей я лучше понял, что такое число обратное. Теперь я знаю, что обратное число получается, если инвертировать данное число и разделить единицу на полученное число. Примеры, которые приведены в статье, помогли мне лучше усвоить материал. Теперь я понимаю, что обратное число для 5, например, будет 0,2, так как 1 разделить на 5 равно 0,2. Большое спасибо автору за ясное объяснение! Теперь я гораздо увереннее в своих знаниях по математике. Буду ждать новых интересных статей!
Отличная статья! Я всегда интересовалась математикой, но понятие обратного числа мне еще не совсем понятно. Благодаря этой статье я наконец-то освоила эту тему. Теперь я знаю, что обратное число — это число, которое при умножении на исходное дает единицу. Я ознакомилась с примерами, которые приведены в статье, и они помогли мне лучше понять это понятие. Теперь я смогу применять его в решении математических задач. Спасибо за доступное объяснение! Я буду рекомендовать эту статью своим друзьям, которые тоже интересуются математикой.