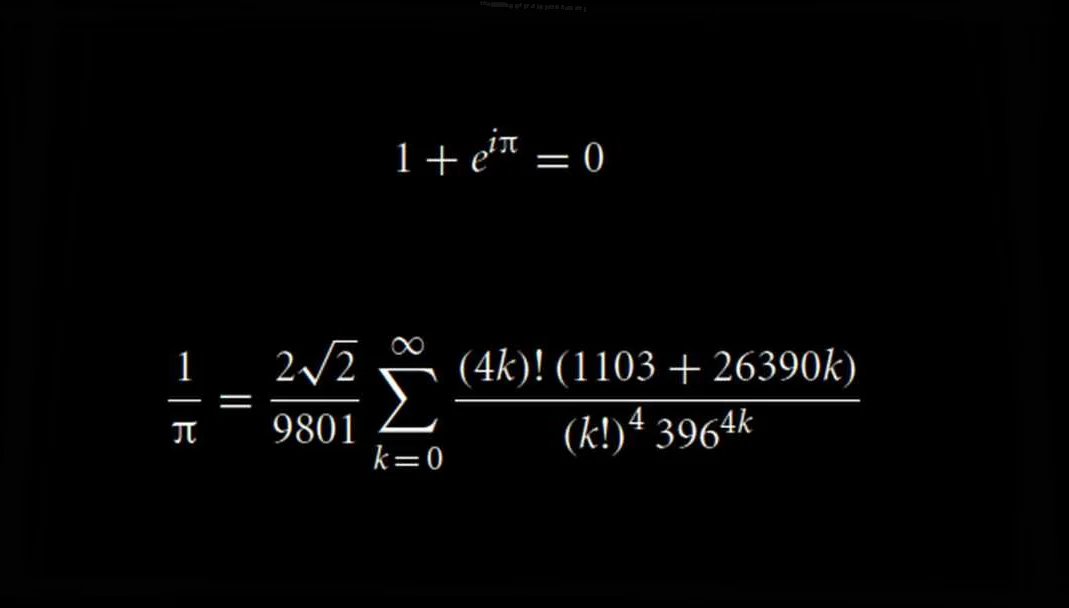Что значит буква «е» в математике наоборот: объяснение и примеры

Узнайте, что означает э в математике наоборот и как его можно использовать в решении задач. Понятное объяснение и примеры из реальной жизни.

В математике существует множество чисел, которые имеют различные свойства и связи с другими числами. Одно из таких чисел — ‘e’, является иррациональным числом, примерно равным 2,71828.

Одним из самых интересных свойств числа ‘e’ является его обратное число, которое обозначается как ‘1/e’. Обратное число ‘e’ — это число, у которого произведение с числом ‘e’ дает единицу. То есть, ‘e’ * ‘1/e’ = 1.

Обратное число ‘e’ широко используется в математике, науке и инженерии. Например, оно используется в экономике для вычисления процентной ставки и в физике для определения периода колебаний электрических цепей.

Обратное число ‘e’ имеет также много интересных свойств, связанных с числами Фибоначчи, функциями и производными. В данной статье мы более подробно рассмотрим это число и его свойства, чтобы более полно понять его значение в математике и научных приложениях.

Обратное число ‘e’ в математике: полное объяснение

Число ‘e’ в математике является одним из наиболее естественных и важных констант. А ее обратное число, обозначаемое как 1/e, также играет важную роль в различных математических задачах и приложениях.

Чтобы понять значение обратного числа ‘e’, нужно сначала разобраться, что представляет собой число ‘e’. ‘e’ является математической константой, которая равна примерно 2,71828. Это число встречается во многих областях науки, включая статистику, физику и экономику.

В математике, число ‘e’ используется, чтобы выразить экспоненциальный рост. Другими словами, если рассмотреть функцию f(x) = e^x, то значение f(x) увеличивается очень быстро с ростом x. Эта функция встречается во многих приложениях, включая решение дифференциальных уравнений и описания процессов роста или распада.

Теперь, когда мы понимаем значение числа ‘e’, мы можем обсудить его обратное значение, 1/e. Это значение также играет важную роль в математике, особенно в тех случаях, когда нужно решить задачи, связанные с вероятностными распределениями и статистикой.

Одно из наиболее известных применений числа 1/e в статистике — это число Эйлера-Маскерони. Оно вычисляется как разность между серии гармонических чисел и натурального логарифма от n, а затем деленного на число ‘e’. Это значение встречается во многих формулах статистики, таких как при оценке дисперсии выборки или при работе с тестами на нормальность распределения.

Также стоит отметить, что число 1/e является приблизительно равным вероятности того, что случайно выбранный объект не попадет в определенный диапазон значений. Это свойство важно при работе с экспоненциальными распределениями и имеет большое практическое применение в экономике и финансах.

Видео по теме:

Что такое число ‘e’?

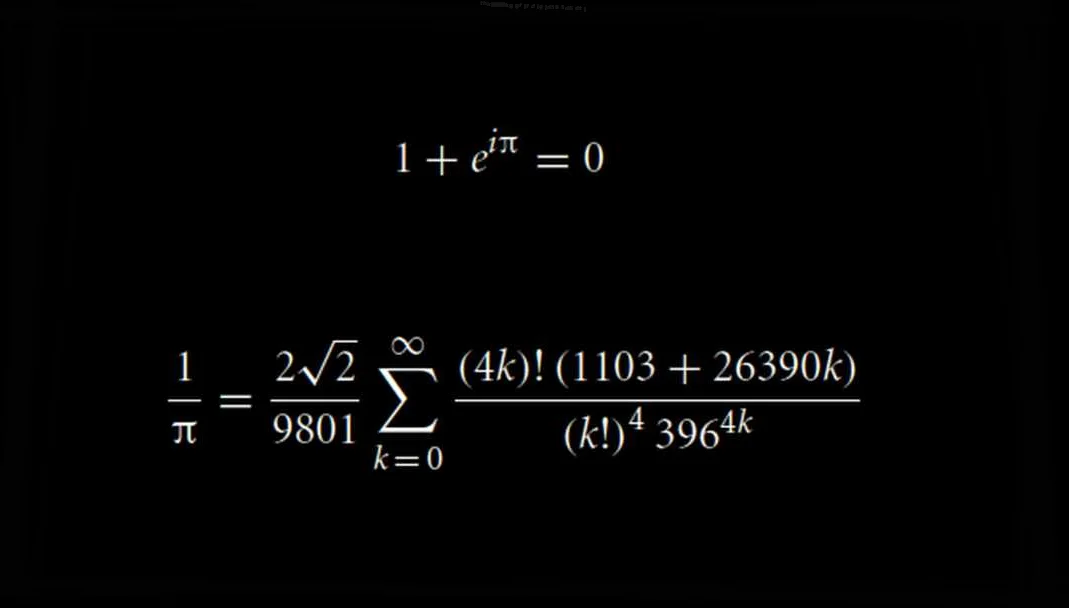
Число ‘e’ является одним из основных математических констант. Оно примерно равно 2,71828.

Число ‘e’ возникает в различных областях математики, физики, экономики и техники. Оно является основой натурального логарифма и экспоненциальной функции.

Константа ‘e’ определяется следующим образом: единица сложенная с бесконечной суммой 1/1!, 1/2!, 1/3!, 1/4!, …

Число ‘e’ имеет много интересных свойств и приложений. Например, оно позволяет описывать процессы экспоненциального роста или убывания.

Также, число ‘e’ является базовым параметром в формулах, описывающих финансовые процессы (например, сложный процент).

Обратно число ‘e’ определяется как 1/e и используется для преобразования логарифма основания ‘e’ к логарифму по основанию 10 или любому другому, разумному основанию.

Очень часто число ‘e’ появляется в приложениях, связанных с вероятностью и статистикой.

Константа ‘e’ является важным элементом в многих областях математики и физики. Понимание ее свойств и возможностей может значительно облегчить решение различных задач и задерживается на курсах математики и других дисциплин.

Какие свойства у числа ‘e’?

Число ‘e’ имеет ряд уникальных свойств, которые делают его важным математическим константой. Одно из наиболее заметных свойств ‘e’ — это то, что оно является базисом натурального логарифма. Это означает, что экспонента ‘e’ — единственная константа, которая имеет производную, равную самому себе, то есть производную e^x является еще одна e^x.

Кроме того, число ‘e’ является нерациональным числом, и его десятичное представление не имеет периодической последовательности. Как таковое, ‘e’ является неразрешимой константой, но его можно приблизительно вычислить с помощью ряда Тейлора.

Число ‘e’ также появляется в множестве других математических формул и уравнений, включая формулу для продольной волны на струне и формулу для расчета скорости при свободном падении. Оно также служит базисом для выведения других геометрических фигур, таких как жгутик Рамануджана и числовые спирали.

Число ‘e’ имеет также множество свойств, которые делают его полезным для различных областей науки и инженерии. Использование ‘e’ в финансовой математике и теории вероятности является общепринятым, а он также играет важную роль в квантовой механике, электротехнике и других дисциплинах.

• Базис натурального логарифма
• Нерациональное число с непериодической последовательностью
• Появляется в множестве математических формул и уравнений
• Полезен для различных областей науки и инженерии

В чем заключается обратное число ‘e’?

Число ‘e’ – это математическая постоянная, которая является основанием натурального логарифма. Ее значение приблизительно равно 2,71828. Обратное число ‘e’ – это число, которое при умножении на ‘e’ дает единицу. Иными словами, обратное число ‘e’ – это 1/’e’.

В многочисленных приложениях математики, физики и инженерии число ‘e’ и его обратное имеют важное значение. Например, при вычислении процентных ставок в финансовой математике используется формула для расчета сложных процентов, в которую входит постоянная ‘e’. Кроме того, число ‘e’ часто встречается в задачах, связанных с теорией вероятностей и статистикой.

Обратное число ‘e’ также имеет интересные свойства. Например, оно является собственным числом для матрицы, образующей множество операторов, непрерывных на бесконечности. Кроме того, обратное число ‘e’ является решением многих дифференциальных уравнений, что делает его важным инструментом в области прикладной математики.

В целом, числа ‘e’ и 1/’e’ – это важные константы, которые имеют широкое применение в различных областях. Понимание их свойств и возможностей позволяет более эффективно использовать их в практических задачах.

Как вычисляется обратное число ‘e’?

Обратное число ‘e’ вычисляется путем взятия обратного значения константы ‘e’, то есть 1/e. Эта операция может быть выполнена с помощью калькулятора или программного обеспечения, имеющего функцию вычисления обратного значения.

Для вычисления обратного числа ‘e’ вручную, необходимо использовать формулу:

1/e = 0.36787944117…

Это значение является бесконечной дробью и может быть представлено с разной точностью, в зависимости от требований задачи.

Также можно использовать таблицы обратных значений, которые содержат заранее вычисленные значения обратных чисел для различных констант, в том числе и для числа ‘e’.

Где используется обратное число ‘e’ в математике?

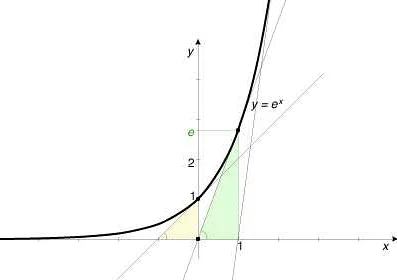
Число ‘e’ — это единица из базовых математических констант, используемых в науке и технике. Оно появляется в различных областях математики, включая анализ, дифференциальные уравнения, теорию вероятностей и многие другие.

Но где именно используется обратное число ‘e’? Ответ на этот вопрос достаточно прост: обратное число ‘e’ — это $1/e$, и оно встречается в тех же областях математики, что и само число ‘e’.

Приложения обратного числа ‘e’:

1. Функция экспоненциального затухания: в общем случае, ее формула выглядит как y = Ae^(-t/RC), где A — амплитуда, t — время, RC — время постоянной зарядки. Обратное число ‘e’ используется в этой формуле как уровень затухания за фиксированный промежуток времени.
2. Формула Самарского-Куранта для численного решения уравнений распространения волн: эта формула используется для решения дифференциальных уравнений в частных производных. В ней обратное число ‘e’ играет роль критического значения для шага по времени при решении уравнения.
3. Процентная функция и бесконечность: когда количество инкрементов стремится к бесконечности, обратное число ‘e’ появляется как коэффициент, определяющий предел процентной функции.

Таким образом, обратное число ‘e’ встречается в различных областях математики, и его применение может иметь многие разнообразные приложения.

Как работает обратное число ‘e’ в финансовой математике?

Обратное число ‘e’ имеет важное значение в финансовой математике. Он используется для расчета накопительного процента, чтобы определить, сколько нужно вложить денег сегодня, чтобы получить определенную сумму в будущем.

Для использования обратного числа ‘e’ в финансовой математике необходимо знать основные формулы, такие как формула сложного процента, формула накопительного процента и формула дисконтирования денежных потоков.

Обратное число ‘e’ также используется для расчета эффективной процентной ставки, которая включает не только проценты, но и другие составляющие, такие как комиссии и другие расходы. Это позволяет получить более точный результат, который учитывает все затраты при инвестировании.

• Пример расчета:

Период	Вложение
1 год	1000 рублей
2 года	? рублей
3 года	3000 рублей

Для расчета суммы на второй год можно воспользоваться формулой накопительного процента:

An = P(1 + r)n

где:

• An — сумма на конец периода;
• P — начальная сумма;
• r — процентная ставка;
• n — количество периодов.

В данном случае начальная сумма — 1000 рублей, количество периодов — 2 года, процентная ставка — 10%, тогда:

A2 = 1000(1 + 0.1)2 = 1210 рублей

Таким образом, для достижения 1210 рублей за два года нужно вложить 1000 рублей по процентной ставке 10%. При расчете использовалось обратное число ‘e’, которое позволяет получить наиболее точный результат.

Какое отношение имеет обратное число ‘e’ к статистике?

Обратное число ‘e’ является константой в математике и распространенно в статистике. Например, оно используется при описании распределения Пуассона и экспоненциального распределения.

В статистике, обратное число ‘e’ может быть использовано для вычисления вероятности того, что некоторое событие произойдет в заданный момент времени, при условии, что вероятность того, что событие произойдет в каждом моменте времени постоянна и независима от предыдущих событий.

Также, константа ‘e’ может также быть использована в качестве базы логарифма при рассмотрении некоторых статистических свойств. Например, при анализе коэффициента корреляции.

Как влияет обратное число ‘e’ на экономику?

Обратное число ‘e’ достаточно распространено в математике и имеет свои применения в экономике. Оно используется для рассчета сложных процентных ставок, что позволяет оценить эффективность инвестиционных проектов и оптимизировать инвестиционные портфели.

Кроме того, обратное число ‘e’ часто используется в экономической теории и при оценке рисков. Например, оно помогает определить оптимальную стратегию игры на фондовом рынке и прогнозировать изменения цен на товары и услуги.

Однако, необходимо понимать, что использование обратного числа ‘e’ в экономике требует знаний и специальных навыков. Неправильные расчеты могут привести к серьезным ошибкам и неэффективным инвестициям.

Таким образом, обратное число ‘e’ является важным инструментом для экономического анализа и принятия решений. Однако, его использование требует профессиональных навыков и знаний, чтобы избежать неправильных расчетов и ошибок.

Как понять значение обратного числа ‘e’ в контексте науки?

Число ‘e’ является одним из фундаментальных математических констант и используется в различных областях науки и техники. Обратное число ‘e’ обозначается как ‘1/e’ и также имеет своё место в научных расчётах.

В математике обратное число ‘e’ используется, например, для нахождения предела функций в бесконечности. Также оно возникает в радиотехнике, где используется для расчёта частотных характеристик фильтров. В физике обратное число ‘e’ используется для расчёта временных констант различных процессов.

Одним из наиболее известных примеров использования обратного числа ‘e’ являются так называемые экспоненциальные функции. Функции этого типа имеют вид ‘f(x) = a^x’, где ‘a’ является постоянной и может принимать значения различных чисел. Когда значение ‘a’ равно ‘e’, функция называется экспоненциальной функцией с основанием ‘e’.

Таким образом, обратное число ‘e’ является важным математическим объектом, используемым в различных областях науки. Понимание его значения и свойств позволяет более точно проводить различные научные расчёты и применять их в практических целях.

Какие примеры существуют для применения обратного числа ‘e’?

Финансы и экономика: Обратное число ‘e’ имеет важное значение в финансовых и экономических расчетах. Например, при расчете процентных ставок по кредитам или инвестициям, обратное число ‘e’ используется для определения того, как быстро инвестиция увеличится в два раза. Также, обратное число ‘e’ может использоваться для измерения времени, необходимого для удвоения начального инвестиционного вклада.

Статистика: Обратное число ‘e’ также играет важную роль в статистике. Например, в экспоненциальном распределении, обратное число ‘e’ используется для определения среднего времени между событиями. Также, обратное число ‘e’ используется при анализе зависимостей в случайных процессах.

Физика: Обратное число ‘e’ используется при расчетах в физике. Например, обратное число ‘e’ используется при расчетах радиоактивного распада и распространения звука в пространстве.

Криптография: Обратное число ‘e’ является одним из параметров при шифровке данных с помощью алгоритма RSA. Например, в RSA-шифровании, обратное число ‘e’ используется для определения открытого ключа, который может использоваться для расшифровки сообщений.

Биология: Обратное число ‘e’ также может использоваться в биологических расчетах. Например, в модели Джима Кроу, которая описывает, как изменяется частота генов в популяции, обратное число ‘e’ используется для определения скорости изменения частот генов.

Таким образом, обратное число ‘e’ находит применение в различных областях знаний и является важным математическим понятием для многих расчетов и моделей.

Как использовать обратное число ‘e’ для решения задач?

Обратное число ‘e’ может быть использовано для решения различных математических задач в науке и инженерии. Оно часто используется в задачах экономики, статистики и физики. Одним из наиболее распространенных применений обратного числа ‘e’ является вычисление процентного роста или уменьшения прироста численности в различных процессах.

Для примера, рассмотрим следующую задачу: «Если население некоторого города увеличивается на 2% ежегодно, то через сколько лет численность населения увеличится вдвое?» Для решения этой задачи мы можем использовать обратное число ‘e’.

Для начала, необходимо выразить увеличение населения в терминах процентов. Для этого мы можем использовать формулу процентного роста:

r = (100 + p) / 100

где r — коэффициент роста, а p — процентный прирост. Для данной задачи, p = 2, поэтому r = 1.02.

Далее, мы можем использовать обратное число ‘e’ для вычисления времени, за которое население города увеличится вдвое:

t = ln(2) / ln(r)

где t — количество лет, необходимых для удвоения численности населения.

Здесь, ln — это натуральный логарифм, обозначенный как loge, и используется для вычисления степени, в которую необходимо возложить число ‘e’, чтобы получить данный аргумент. Для данной задачи, логарифм числа ‘e’ равен 1, а логарифм коэффициента роста равен 0.0198. Подставив эти значения в формулу, мы получим t = 35 лет (округленно до целого числа).

Таким образом, использование обратного числа ‘e’ может значительно упростить решение математических задач, связанных с процентным ростом или уменьшением, и позволить получить точные результаты с минимальным количеством вычислений.

Вопрос-ответ:

Что такое обратное число ‘e’?

Обратное число ‘e’ — это число, при умножении на которое число ‘e’ равно единице. Формально это обозначается как e^(-1) и равно примерно 0,36. Обратное число ‘e’ является особенно важным в математическом анализе, теории вероятностей и других областях, так как оно связано с натуральным логарифмом и экспонентой.

Можно ли представить обратное число ‘e’ в виде бесконечной десятичной дроби точно?

Нет, так как обратное число ‘e’ является иррациональным числом, то есть его десятичное представление является бесконечной десятичной дробью, которая никогда не повторяется и не может быть записана как отношение двух целых чисел.

Как связано обратное число ‘e’ с натуральным логарифмом?

Обратное число ‘e’ связано с натуральным логарифмом следующим образом: натуральный логарифм числа x обозначается как ln x, и определяется как интеграл от 1 до x функции 1/t dt. Натуральный логарифм числа ‘e’ равен единице, то есть ln e = 1. Обратно, для любого числа y, e в степени ln y равно y, то есть e^(ln y) = y. Эта связь между натуральным логарифмом и обратным числом ‘e’ является основой многих вычислительных и аналитических методов в математике и статистике.

Как вычислить обратное число ‘e’ на калькуляторе?

Обратное число ‘e’ может быть вычислено на большинстве научных калькуляторов посредством нажатия кнопки ‘e^x’, затем ввода ‘-1’ и нажатия кнопки равно. Результатом будет приблизительно 0,36.

Можно ли использовать обратное число ‘e’ в повседневной жизни?

Обратное число ‘e’ не имеет прямого применения в повседневной жизни, однако его свойства и применения могут быть полезными при изучении математики, физики, статистики и других научных дисциплин.