Что означает две скобки в математике

Две скобки в математике используются для обозначения операции умножения или для обозначения приоритета выполнения операций в выражении. Узнайте, как использовать скобки в математике и как правильно интерпретировать их значение.

Математика является одной из основных наук, которая изучает числа, структуры, пространства и изменения. В математике часто используются различные символы и обозначения, имеющие свои уникальные значения и правила использования. Одним из таких символов являются скобки.

Скобки в математике используются для группировки выражений, указания приоритета операций, задания интервалов и множеств, а также для обозначения функций. В математике существует несколько типов скобок, но наиболее распространены и широко используются круглые скобки – ( ).

Круглые скобки в математике обозначают группировку выражений и указывают на то, что выражение, находящееся внутри скобок, должно быть выполнено первым. Они также используются для обозначения аргументов функций. Например, выражение (2+3) означает, что сначала нужно выполнить сложение чисел 2 и 3, а затем полученный результат можно использовать в дальнейших вычислениях.

Использование скобок в математике имеет свои строгие правила и соглашения, которые необходимо соблюдать для корректного выполнения математических операций. Неправильное использование скобок может привести к неправильным результатам и недопониманию в математических выражениях и формулах.

В заключение, скобки являются важным инструментом в математике, позволяющим указывать порядок выполнения операций, группировать выражения и обозначать аргументы функций. Правильное использование скобок является неотъемлемой частью математического анализа и решения задач в различных областях. Поэтому знание основных принципов использования скобок позволяет более точно и четко формулировать и решать математические задачи.

Значение двух скобок в математике: основные принципы и применение

В математике скобки используются для группировки и упорядочивания операций. Приоритет операций и порядок их выполнения могут быть изменены с помощью скобок, что позволяет получать различные значения и результаты выражений.

Две скобки, обычно представленные как пара символов «(» и «)», называются круглыми скобками. Они являются самым распространенным типом скобок в математике и имеют ряд основных принципов использования.

Основной принцип использования круглых скобок состоит в том, что все выражение, заключенное внутри скобок, считается единым целым и выполняется в первую очередь. Это позволяет указать порядок выполнения операций и явно указать, какие значения должны быть вычислены и группированы вместе.

Применение круглых скобок в математике может быть разнообразным. Они могут использоваться для определения порядка операций, для управления приоритетом вычислений и для создания более сложных выражений. Например, выражение (2 + 3) * 4 означает, что сначала выполняется операция сложения 2 и 3, а затем полученное значение умножается на 4.

Круглые скобки также могут использоваться для группировки переменных и значений, что облегчает чтение и понимание математических выражений. Например, выражение (a + b) * c означает, что сначала значения a и b складываются, а затем полученная сумма умножается на значение c. Без скобок это выражение может быть непонятным и приводить к неправильному результату.

Круглые скобки также используются в математике для обозначения функций и аргументов. Например, функция f(x) означает, что значение x подставляется в функцию f для вычисления результата. Скобки здесь указывают на то, что значение x является аргументом функции и должно быть передано для вычисления.

В заключение, круглые скобки в математике играют важную роль в определении порядка выполнения операций и группировке значений. Они позволяют создавать более сложные выражения, указывать приоритеты и управлять вычислениями. Правильное использование скобок помогает избежать путаницы и получить точные и корректные результаты вычислений.

Определение и назначение скобок в математике

Существуют различные типы скобок, такие как круглые скобки ( ), квадратные скобки [ ], фигурные скобки { }, и ангулярные скобки < >. Каждый тип скобок имеет свое назначение и правила использования в математике.

Одной из главных функций скобок является изменение приоритета операций в математических выражениях. Выражения, заключенные в скобки, выполняются в первую очередь, а затем результат используется для выполнения остальной части выражения.

Скобки также используются для обозначения интервалов в математике. Например, круглые скобки могут использоваться для обозначения открытого интервала, а квадратные скобки — для обозначения закрытого интервала. Это позволяет более точно определить множество значений переменной.

Кроме того, скобки используются для обозначения математических функций и операций. Например, круглые скобки вокруг аргумента функции обозначают, что этот аргумент является входным значением функции. Также скобки используются для обозначения операций сложения, вычитания, умножения и деления.

Использование скобок в математике является важным элементом для обеспечения правильности и ясности математических выражений и формул. Правильное использование скобок помогает избежать двусмысленности и ошибок при выполнении математических операций.

Круглые скобки: основные правила использования

В математике круглые скобки используются для обозначения группировки выражений и приоритета операций. Они позволяют указать порядок выполнения действий в выражении.

Основные правила использования круглых скобок:

ПравилоПримерРезультат

Группировка выражений	(2 + 3) * 4	20
Изменение приоритета операций	2 * (3 + 4)	14
Создание функций и вызовов функций	sin(0)	0
Обозначение аргументов в математических функциях	log(10, 100)	2
Указание интервалов	[1, 5]	множество всех чисел от 1 до 5

Круглые скобки могут быть использованы вместе с другими скобками для создания более сложных выражений. Например, можно использовать круглые скобки внутри квадратных скобок для указания элементов массива или внутри фигурных скобок для создания объектов.

Правильное использование круглых скобок позволяет избежать неоднозначностей и уточнить смысл математического выражения.

Квадратные скобки: принципы применения

В математике квадратные скобки [ ] имеют различные принципы применения в зависимости от контекста. Они могут использоваться для обозначения множеств, матриц, индексов, степеней и др.

Одним из основных принципов использования квадратных скобок является обозначение множества. Квадратные скобки могут использоваться для указания конкретных элементов, принадлежащих множеству. Например, [1, 2, 3] обозначает множество, содержащее числа 1, 2 и 3.

Квадратные скобки также могут использоваться для обозначения матриц. В этом случае элементы матрицы разделяются запятыми и заключаются в квадратные скобки. Например:

[1, 2]

[3, 4]

Квадратные скобки могут также использоваться для обозначения индексов. Индекс обозначает положение элемента в последовательности или массиве. Например, А[2] обозначает элемент с индексом 2 в массиве А.

Кроме того, квадратные скобки могут использоваться для обозначения степени. Например, 2[3] означает число 2, возведенное в степень 3.

Таким образом, квадратные скобки в математике имеют различные принципы применения и используются для обозначения множеств, матриц, индексов, степеней и других математических операций.

Фигурные скобки: особенности и область применения

Основная особенность фигурных скобок заключается в их гибкости и многофункциональности. Они могут использоваться для обозначения множеств, состоящих из различных элементов, а также для описания групп элементов, которые имеют общие свойства или характеристики.

Фигурные скобки также часто применяются для указания условий, при которых выполняется определенное действие или применяется определенное правило. Например, в математической нотации фигурные скобки могут использоваться для обозначения условий в определении функций или для указания диапазонов значений переменных.

В программировании фигурные скобки используются для обозначения блоков кода, которые должны быть выполнены вместе. Они служат для группировки инструкций или операций и упрощают чтение и понимание программного кода.

Итак, фигурные скобки являются важным инструментом в математике и программировании, позволяя группировать элементы, указывать условия и структурировать информацию. Их использование помогает создавать логические конструкции и облегчает понимание и анализ сложных систем и данных.

Угловые скобки: роль в математике и преимущества

Угловые скобки, которые выглядят как символы «», играют важную роль в математике и имеют несколько применений.

Во-первых, угловые скобки могут использоваться для обозначения углов. Например, если у нас есть угол ABC, то его можно записать как ∠ABC. Это помогает нам лучше понимать геометрические фигуры и связанные с ними понятия.

Во-вторых, угловые скобки используются в математических выражениях для обозначения неравенства. Например, выражение 2 < 3 означает, что 2 меньше 3. Также угловые скобки могут использоваться для обозначения неравенства в другом направлении, например, 5 > 2 означает, что 5 больше 2.

Использование угловых скобок в математике имеет свои преимущества. Во-первых, они помогают нам лучше визуализировать и понять геометрические фигуры и объекты. Во-вторых, они помогают упростить запись математических выражений и неравенств, делая их более компактными и понятными.

В заключение, угловые скобки играют важную роль в математике, помогая нам лучше понять геометрические фигуры и записывать математические выражения и неравенства более компактно и понятно.

Скобки в уравнениях: правила и примеры использования

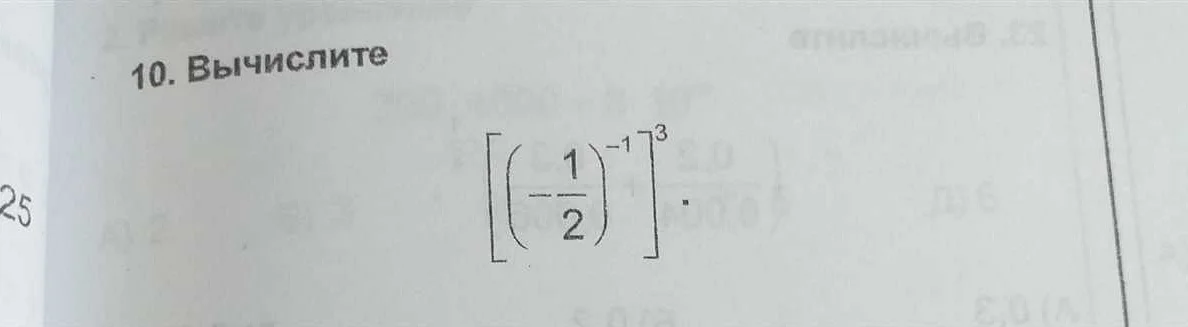
Правила использования скобок:

1. Круглые скобки ( )

Круглые скобки используются для группировки операций и изменения порядка их выполнения. Выражения, заключенные в круглые скобки, вычисляются прежде всего. Например:

2 * (3 + 4) будет равно 14, так как сначала выполняется операция внутри скобок (3 + 4), а затем происходит умножение.

2. Квадратные скобки [ ]

Квадратные скобки также используются для группировки операций, но их основное применение связано с обозначением индексов и массивов. Например:

[2 + 3] * 4 будет равно 20, так как сначала выполняется операция внутри квадратных скобок (2 + 3), а затем происходит умножение.

3. Фигурные скобки { }

Фигурные скобки обычно используются для обозначения множеств или наборов элементов. Например:

{1, 2, 3} обозначает множество чисел 1, 2 и 3.

Примеры использования скобок в уравнениях:

5 * (2 + 3) — 4

В этом уравнении сначала выполняется операция внутри круглых скобок (2 + 3), затем происходит умножение (5 * 5), а затем вычитание (25 — 4). Результат будет равен 21.

3 + [2 * (4 — 1)]

Здесь сначала выполняется операция внутри круглых скобок (4 — 1), затем умножение (2 * 3), а затем сложение (3 + 6). Результат будет равен 9.

Правильное использование скобок в уравнениях важно для получения правильных результатов и понимания математических выражений. Знание правил и примеров использования скобок поможет вам более точно и эффективно решать уравнения и задачи.

Скобки в функциях: значение и влияние на результат

В математике скобки играют важную роль в определении порядка операций и приоритета выполнения функций. Скобки позволяют группировать операции и указывают компьютеру, какие действия следует выполнять в первую очередь.

Одна из основных функций скобок в математике — задать порядок действий в выражении. Например, в выражении (2 + 3) * 4 скобки вокруг суммы указывают, что сначала нужно выполнить операцию сложения, а затем умножение. Без скобок результат был бы другим: 2 + 3 * 4 = 14.

Скобки также используются для указания аргументов функций. В математике функция представляет собой набор инструкций, которые принимают один или несколько аргументов и возвращают результат. Например, функция sqrt(x) используется для нахождения квадратного корня числа x. Аргумент функции указывается в скобках: sqrt(9) = 3.

Важно помнить, что неправильное использование скобок в функциях может привести к некорректным результатам. Например, если забыть закрыть скобки, то компьютер будет воспринимать все, что следует за открывающей скобкой, как аргумент функции. Также следует обратить внимание на правильность расстановки скобок при группировке операций, чтобы избежать двусмысленности и получить корректный результат.

Вопрос-ответ:

Зачем в математике используются две скобки?

Две скобки в математике используются для обозначения приоритетов операций и для группировки частей выражения.

Какие основные принципы применяются при использовании двух скобок в математике?

Основные принципы при использовании двух скобок в математике включают правила приоритетов операций и правила расстановки скобок для правильного выполнения математических выражений.

Какие операции имеют более высокий приоритет в математике при использовании двух скобок?

В математике операции с более высоким приоритетом при использовании двух скобок включают умножение, деление и возведение в степень.

Какие примеры применения двух скобок в математике можно привести?

Примеры применения двух скобок в математике включают вычисление арифметических выражений, решение уравнений, построение графиков функций и проведение математических операций с векторами и матрицами.

Скобки в выражениях: полезные советы и рекомендации

Вот несколько полезных советов и рекомендаций, которые помогут вам использовать скобки в выражениях:

1. Используйте скобки для управления порядком выполнения операций. Если вы хотите, чтобы определенные операции выполнены первыми, заключите их в скобки. Например, выражение (2 + 3) * 4 будет иметь разный результат от выражения 2 + 3 * 4.
2. При использовании нескольких пар скобок, обратите внимание на их правильное расположение. В случае, когда скобки вложены друг в друга, вычисление должно быть проведено с внутренних к внешним скобкам. Например, в выражении (2 + (3 * 4)) сначала выполнится операция во внутренних скобках (3 * 4), а затем результат будет сложен с 2.
3. Избегайте лишних скобок. Иногда можно упростить выражение, убрав ненужные скобки. Например, выражение (x + y) + z можно записать как x + y + z без изменения результата вычислений.
4. Не забывайте использовать скобки в дробях. При записи дробных чисел или выражений с дробными числами, необходимо использовать скобки для явного указания числителя и знаменателя. Например, запись (3/4) * 2 будет иметь разный результат от 3/4 * 2.

Скобки в выражениях играют важную роль в математике, и правильное их использование является ключевым для получения верного результата. Помните эти советы и рекомендации при работе с математическими выражениями, чтобы избежать ошибок и получить правильные ответы.

Видео по теме: