Когда в математике ставятся квадратные скобки а когда круглые

Узнайте, когда в математике необходимо использовать квадратные скобки и когда предпочтительнее использовать круглые. Понимание этих правил поможет вам правильно интерпретировать и записывать математические выражения.

В математике квадратные и круглые скобки являются одними из основных символов, которые используются для обозначения и объединения числовых выражений. Они играют важную роль в математических формулах, уравнениях и выражениях, помогая определить порядок операций и группировать числа и переменные.

Квадратные скобки, обозначаемые символами «[ ]», часто используются для указания интервалов или диапазонов чисел, а также для обозначения матриц и векторов. Они также могут использоваться для выделения отдельных элементов в формулах и уравнениях. Например, [a, b] обозначает интервал чисел от a до b, а [1 2 3] представляет вектор из трех элементов.

Круглые скобки, обозначаемые символами «( )», используются для обозначения приоритета операций и группировки выражений. Они помогают определить порядок выполнения операций в математических выражениях. Например, в выражении (2 + 3) × 4, сначала выполняется операция внутри круглых скобок, а затем умножение. Круглые скобки также могут использоваться для обозначения аргументов функций и выражений в алгебре и анализе.

Важно понимать, что правильное использование квадратных и круглых скобок является неотъемлемой частью математического понимания и коммуникации. Неправильное расположение или пропуск скобок может привести к неверным результатам и непониманию выражений. Поэтому важно быть внимательным и следовать правилам использования скобок в математике.

Итак, квадратные и круглые скобки в математике играют важную роль в определении порядка операций и группировки чисел и переменных. Правильное использование скобок является ключевым для понимания и правильного решения математических задач и уравнений.

Разбираемся в правилах использования квадратных и круглых скобок в математике

В математике квадратные и круглые скобки используются для обозначения определенных операций и приоритетности вычислений. Правильное использование скобок в математических выражениях позволяет более точно определить порядок действий и избежать недоразумений.

Круглые скобки ( ) часто используются для группировки операций и указания приоритета вычислений. Внутри круглых скобок вычисления выполняются в первую очередь. Например, в выражении (2 + 3) * 4 сначала выполняется операция внутри скобок, а затем результат умножается на 4, что дает общий результат равный 20.

Квадратные скобки [ ] часто используются для обозначения интервалов или массивов. Например, [1, 2, 3] обозначает массив из трех элементов, а [0, 10] обозначает интервал чисел от 0 до 10 включительно.

Кроме того, квадратные скобки могут использоваться для обозначения округления числа или дробной части. Например, [x] обозначает округление числа x до ближайшего целого числа, а [x] обозначает наибольшее целое число, не превышающее x.

Правильное использование квадратных и круглых скобок в математике является важной частью вычислений и позволяет более точно определить порядок действий. При использовании скобок следует обратить внимание на их расположение и правильное закрытие каждой пары скобок.

Видео по теме:

Какие скобки используются в математике и зачем?

В математике используются два вида скобок: квадратные и круглые. Оба вида скобок имеют свои особенности и используются для разных целей.

Квадратные скобки [ ] используются в математике для обозначения массивов, векторов и матриц. Они также могут использоваться для обозначения интервалов на числовой прямой. Квадратные скобки могут добавлять ясность и уточнение к математическому выражению.

Круглые скобки ( ) являются наиболее распространенным видом скобок в математике. Они используются для группировки операций и задания порядка выполнения вычислений. Круглые скобки также могут использоваться для обозначения аргументов функций и выражений в алгебраических выражениях.

Использование скобок в математике помогает уточнить и структурировать выражения, делает их более понятными и позволяет корректно выполнять вычисления.

Как правильно использовать круглые скобки в выражениях?

Круглые скобки в математике используются для группировки операций и задания приоритета выполнения действий. Они помогают определить порядок действий и улучшить читаемость выражений.

Основные правила использования круглых скобок:

ПравилоПример

Группировка операций	(2 + 3) * 4 = 20
Задание приоритета	2 + (3 * 4) = 14
Изменение направления операции	8 / (2 + 2) = 2

Важно помнить, что круглыми скобками можно группировать любые операции и выражения, в том числе выражения с использованием других видов скобок.

Правильное использование круглых скобок позволяет избежать неоднозначностей и ошибок при вычислении выражений. Важно придерживаться правил математической нотации и четко указывать порядок выполнения операций.

Как использовать квадратные скобки в математических формулах?

Квадратные скобки в математических формулах используются для обозначения различных математических операций и конструкций. Вот некоторые основные способы использования квадратных скобок в математике:

1. Индексы и степени

Квадратные скобки часто используются для обозначения индексов и степеней. Например, если есть переменная x и её индексом является число 2, то можно записать это как x2. А если переменная x возводится в квадрат, то можно записать это как x2.

2. Массивы и векторы

Квадратные скобки также используются для обозначения массивов и векторов. Например, если есть массив чисел a, то можно записать это как a[1], a[2], a[3], …. А если есть вектор v с координатами x и y, то можно записать это как v = [x, y].

3. Интервалы

Квадратные скобки используются для обозначения интервалов. Например, если нужно записать интервал чисел от 1 до 10 включительно, то можно записать это как [1, 10]. Если нужно записать интервал от 1 до 10, не включая границы, то можно записать это как (1, 10) или 1 < x < 10.

Таким образом, квадратные скобки в математических формулах используются для различных целей, таких как обозначение индексов и степеней, массивов и векторов, а также интервалов.

Правила расстановки скобок в комплексных выражениях

В математике при работе с комплексными выражениями существуют определенные правила по расстановке скобок. Важно соблюдать эти правила, чтобы избежать неправильных результатов и сделать выражение более понятным.

Основное правило заключается в том, что скобки должны быть расставлены в соответствии с приоритетом операций. Например, если в выражении присутствуют операции сложения и умножения, то умножение имеет более высокий приоритет и должно быть выполнено первым. В данном случае, скобки следует расставить вокруг операции умножения.

Другое важное правило — скобки следует расставлять вокруг операндов, которые выступают в качестве аргументов для различных функций. Например, при вычислении тригонометрических функций (синус, косинус и т.д.) необходимо заключать аргументы в круглые скобки.

Если в выражении присутствуют несколько различных операций, то необходимо использовать квадратные скобки для явной указания порядка выполнения операций. Например, если выражение содержит операции сложения, вычитания и умножения, то необходимо расставить скобки вокруг операции умножения, чтобы она была выполнена первой.

Правильная расстановка скобок в комплексных выражениях позволяет избежать неоднозначностей и упрощает понимание выражения. Следуя данным правилам, можно получить корректный результат и избежать ошибок при выполнении математических операций.

Важность точной последовательности скобок в выражениях

В математике точная последовательность скобок в выражениях имеет важное значение. Она определяет порядок выполнения операций, а следовательно, и результат вычисления.

Квадратные и круглые скобки используются для группировки чисел и операций, чтобы указать, какие операции должны быть выполнены в первую очередь. Правильное расположение скобок может изменить результат вычисления.

Квадратные скобки [ ] обычно используются в математических выражениях для обозначения индекса или подстановки значений в функцию. Они также используются для обозначения области действия операции или функции.

Круглые скобки ( ) в математических выражениях используются для обозначения группировки операций или приоритета. Они указывают на то, что операции, находящиеся внутри скобок, должны быть выполнены раньше, чем операции вне скобок.

Неверная последовательность скобок может привести к неправильному результату вычисления. Например, в выражении 3 + 5 * 2 без скобок операция умножения будет выполнена перед операцией сложения, и результат будет равен 13. Однако, если мы добавим скобки и напишем выражение (3 + 5) * 2, результат будет равен 16.

Поэтому важно помнить о правильной последовательности скобок в выражениях и учитывать приоритет операций, чтобы получить точный результат вычисления.

Особенности использования скобок в уравнениях и неравенствах

При решении уравнений и неравенств в математике, правильное использование скобок играет важную роль. Квадратные и круглые скобки используются для группировки выражений и управления порядком операций.

Круглые скобки () обычно используются для указания порядка выполнения операций. Выражения, заключенные в круглые скобки, вычисляются первыми. Например, в уравнении 2 * (3 + 4) = 14, выражение внутри скобок (3 + 4) будет вычислено первым, а затем умножено на 2.

Квадратные скобки [] могут использоваться для обозначения массивов или для указания интервалов. В уравнениях и неравенствах они часто используются для обозначения границ интервалов. Например, [2, 5] обозначает интервал от 2 до 5, включая обе границы.

Ошибки в использовании скобок могут привести к неправильным результатам. Поэтому важно следить за правильным порядком скобок и учитывать их значения при решении уравнений и неравенств.

Использование правильных скобок помогает уточнить и упорядочить математические выражения, делая их более понятными и легкими для анализа и вычисления. Помните, что круглые и квадратные скобки имеют различные значения и следует применять их согласно математическим правилам.

Некоторые примеры использования скобок в математике

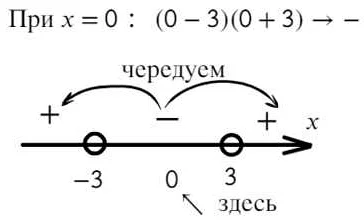
Скобки в математике используются для выделения частей формулы и правил приоритета операций. Они помогают определить порядок вычислений и упрощают запись сложных выражений.

Одним из основных видов скобок являются круглые скобки ( ). Они используются для выделения частей формулы, которые должны быть вычислены первыми. Например:

ВыражениеРезультат

(2 + 3) * 4	20
(6 — 2) / 2	2

Квадратные скобки [ ] используются в математике для выделения частей формулы, которые должны быть вычислены в первую очередь, но при этом имеют особое значение или функцию. Например:

ВыражениеРезультат

[2 + 3] * 4	20
[6 — 2] / 2	2

Фигурные скобки { } могут использоваться в математике для обозначения множеств или для выделения группы элементов. Например:

ВыражениеРезультат

{1, 2, 3} ∪ {3, 4, 5}	{1, 2, 3, 4, 5}
{x | x > 0}	множество положительных чисел

Кроме того, могут использоваться угловые скобки < > для обозначения интервалов или для обозначения отношений. Например:

ВыражениеРезультат

x < 5	истина, если x меньше 5
0 <= x <= 10	истина, если x находится в интервале от 0 до 10 включительно

Правильное использование скобок в математике является важным навыком, который помогает установить правильный порядок вычислений и понять значение выражения.

Как избежать ошибок при использовании скобок в выражениях?

Совет	Пояснение
1.	Правильно расставляйте круглые скобки.
2.	Используйте квадратные скобки для обозначения отрезков или массивов.
3.	Помните о приоритете операций.
4.	Не забывайте закрывать все открывающие скобки.
5.	Учитывайте правила скобочной структуры.
6.	Проверяйте выражения на баланс скобок.

Следуя этим советам, вы сможете избежать ошибок при использовании скобок в математических выражениях и получить правильные результаты.

Вопрос-ответ:

Какие правила использования скобок в математике существуют?

Существуют различные правила использования скобок в математике. Одно из основных правил — использование круглых скобок для обозначения приоритета операций. Например, если в выражении есть операции сложения и умножения, то сначала выполняются операции внутри круглых скобок, затем умножение, а потом сложение. Квадратные скобки и фигурные скобки также могут использоваться для обозначения приоритета операций или для группировки элементов внутри выражения.

Какая разница между круглыми и квадратными скобками?

Основная разница между круглыми и квадратными скобками в математике заключается в их функции. Круглые скобки обычно используются для обозначения приоритета операций, тогда как квадратные скобки часто используются для обозначения группировки элементов или для обозначения матриц и векторов. Например, в выражении (3 + 4) * 5, круглые скобки указывают, что сначала нужно выполнить операцию сложения, а затем умножение.

Как использовать скобки для обозначения приоритета операций?

Для обозначения приоритета операций в математическом выражении используются круглые скобки. Выражения, заключенные в круглые скобки, имеют более высокий приоритет и выполняются раньше, чем операции вне скобок. Например, в выражении 2 * (3 + 4), операция внутри круглых скобок (3 + 4) будет выполнена первой, а затем результат будет умножен на 2.

Когда нужно использовать квадратные скобки?

Квадратные скобки в математике могут использоваться в различных контекстах. Одно из основных применений квадратных скобок — это обозначение группировки элементов или для обозначения матриц и векторов. Например, [1, 2, 3] обозначает вектор с элементами 1, 2 и 3. Квадратные скобки также могут использоваться для обозначения интервалов на числовой прямой, например [1, 5] обозначает все числа от 1 до 5 включительно.

Можно ли использовать фигурные скобки в математике?

Да, фигурные скобки также могут использоваться в математике. Они обычно используются для обозначения множеств или для задания условий в математических уравнениях. Например, {1, 2, 3} обозначает множество с элементами 1, 2 и 3. Фигурные скобки также могут использоваться для задания условий, например {x | x > 0} обозначает множество всех чисел x, которые больше нуля.