Что значит в математике на и в

Узнайте, что означают слова «на» и «в» в математике и как они используются в разных контекстах. Исследуйте их значения и примеры применения, чтобы лучше понять эти понятия и их роль в математике.

Математика — это наука о числах, формулах и отношениях между ними. В процессе изучения математики вы столкнетесь с различными символами и обозначениями, которые имеют свои специфические значения. Два таких символа — «и» и «в» — являются основными в математике и используются для описания отношений и связей между числами.

Символ «и» в математике обычно используется для объединения двух или более условий или фактов. Он означает, что все условия должны быть истинными одновременно. Например, если у нас есть утверждение «x > 5 и y < 10», это означает, что оба условия — «x больше 5» и «y меньше 10» — должны быть истинными для выполнения всего утверждения.

Символ «в» в математике обычно используется для указания принадлежности элемента к некоторому множеству. Он может быть использован, например, для обозначения, что число принадлежит определенному интервалу или множеству значений. Например, если у нас есть утверждение «x в [0, 10)», это означает, что число x принадлежит полуоткрытому интервалу от 0 до 10, где 0 включается, а 10 исключается.

Важно понимать, что символы «и» и «в» имеют специфическое значение в математике и могут отличаться от их использования в естественном языке. Правильное понимание и использование этих символов поможет вам более точно формулировать и решать математические задачи.

Математика: понятие «и» и «в»

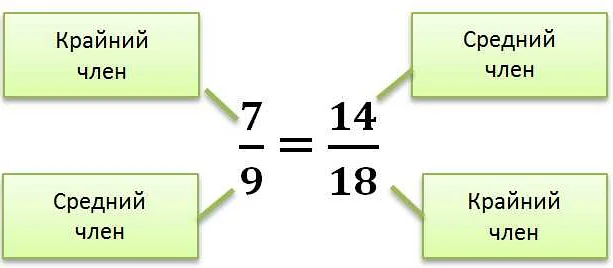
Символ «и» обозначается знаком «&», который означает объединение элементов множества. Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то объединение этих множеств обозначается как A & B и будет содержать все элементы, которые присутствуют в обоих множествах: A & B = {3}.

Символ «в» обозначается знаком «∈», который означает принадлежность элемента к множеству. Например, если у нас есть множество A = {1, 2, 3}, то можно сказать, что число 2 принадлежит множеству A, обозначая это как 2 ∈ A.

Таким образом, понятие «и» и «в» в математике играют важную роль при работе с множествами и указывают на их связь и принадлежность элементов.

Значение «и» и «в» в математике

В математике символы «и» и «в» используются для обозначения отношений и связей между объектами.

Символ «и» обычно используется для обозначения логической конъюнкции или объединения. Например, если у нас есть высказывания А и В, то их объединение обозначается символом «и».

Символ «в» обычно используется для обозначения принадлежности или включения одного объекта в другой. Например, если у нас есть множество А и элемент В, то мы можем сказать, что В принадлежит множеству А или что В входит в множество А.

Для более точного понимания, рассмотрим примеры:

Пример с использованием символа «и»:

Если у нас есть высказывания «сегодня солнечно» и «температура высокая», то их объединение будет выглядеть так: «сегодня солнечно и температура высокая».

Пример с использованием символа «в»:

Если у нас есть множество целых чисел и элемент 5, то мы можем сказать, что 5 принадлежит множеству целых чисел или что 5 входит в множество целых чисел.

Примеры использования «и» и «в» в математике

Оператор «и» в математике используется для объединения условий или свойств двух или более объектов. Например, если у нас есть два множества A и B, то запись «x ∈ A и x ∈ B» означает, что элемент x принадлежит как множеству A, так и множеству B.

Оператор «в» в математике используется для указания принадлежности элемента к определенному множеству. Например, запись «x ∈ A» означает, что элемент x принадлежит множеству A.

Рассмотрим пример. Пусть у нас есть два множества A = {1, 2, 3} и B = {2, 3, 4}. Запишем объединение этих множеств с помощью оператора «и»:

A ∪ B = {x | x ∈ A и x ∈ B} = {2, 3}

Таким образом, объединение множеств A и B состоит из элементов, которые принадлежат и множеству A, и множеству B.

Теперь рассмотрим пример использования оператора «в». Пусть у нас есть множество A = {1, 2, 3}. Запишем условие для принадлежности элемента 2 множеству A:

2 ∈ A

Таким образом, элемент 2 принадлежит множеству A.

Математические операции с использованием «и» и «в»

В математике символы «и» и «в» используются для обозначения различных операций.

Операция «и» используется для объединения двух условий или множеств. Например, если у нас есть два условия A и B, то их объединение обозначается как A и B. Это означает, что оба условия должны быть истинными, чтобы всё выражение было истинным. Например, если A — «x > 5» и B — «x < 10», то выражение «x > 5 и x < 10» будет истинным только в том случае, когда x будет больше 5 и меньше 10 одновременно.

Операция «в» используется для указания диапазона значений или интервала. Например, если у нас есть условие «x в [a, b]», то это означает, что x должен находиться в диапазоне от a до b включительно. Например, если a = 1 и b = 5, то условие «x в [1, 5]» будет выполнено только в том случае, когда x будет равно 1, 2, 3, 4 или 5.

Таким образом, операции «и» и «в» позволяют нам компактно и точно задавать условия и операции в математике.

Сходства и различия между «и» и «в» в математике

В математике символы «и» и «в» играют разные роли, но также имеют некоторые сходства.

Первое сходство состоит в том, что оба символа могут использоваться для обозначения принадлежности элемента множеству. Например, если у нас есть множество A = {1, 2, 3}, то можно записать:

1 в A (1 принадлежит множеству A)

2 в A (2 принадлежит множеству A)

3 в A (3 принадлежит множеству A)

Второе сходство заключается в использовании символа «и» для обозначения логической операции «и». Например, если у нас есть два утверждения P и Q, то можно записать:

P и Q (P и Q)

Это означает, что оба утверждения P и Q должны быть истинными, чтобы выражение P и Q было истинным.

Однако, существуют и различия между символами «и» и «в» в математике.

Первое различие заключается в том, что символ «и» используется для обозначения операции «и» между элементами множеств, а символ «в» используется для обозначения принадлежности элемента множеству.

Второе различие состоит в том, что символ «и» может использоваться для соединения более чем двух утверждений, в то время как символ «в» обычно используется для обозначения принадлежности одного элемента множеству.

Например, можно записать:

P и Q и R (P и Q и R)

но нельзя записать:

1 в A и B (1 принадлежит множеству A и B)

Таким образом, символы «и» и «в» имеют сходства и различия в математике, и их использование зависит от контекста и задачи.

Важность понимания «и» и «в» в математике

Слово «и» в математике используется для объединения двух или более элементов или условий. Например, если у нас есть два числа, например, 5 и 3, мы можем объединить их с помощью слова «и» и записать это как «5 и 3». Такое объединение помогает нам описать ситуации, когда необходимо выполнение нескольких условий одновременно.

Слово «в» в математике используется для указания принадлежности или включения элемента в какое-либо множество или диапазон. Например, если у нас есть множество чисел от 1 до 10, мы можем указать, что число 5 принадлежит этому множеству, используя слово «в» и записать это как «5 в множестве от 1 до 10». Такое указание помогает нам определить, к каким множествам относится тот или иной элемент.

Понимание этих различий в использовании слов «и» и «в» является важным, так как неправильное использование этих слов может привести к неправильным выводам и ошибкам при работе с математическими выражениями. Для успешного решения задач и понимания математических концепций необходимо уметь верно интерпретировать и задавать отношения между элементами и условиями.

Таким образом, осознание значений и применений слов «и» и «в» в математике является ключевым фактором для успешного усвоения этой науки и корректного решения задач.

Практическое применение «и» и «в» в решении задач

В математике, использование логических операторов «и» и «в» может быть очень полезным при решении различных задач. Эти операторы позволяют комбинировать условия и устанавливать связь между различными элементами.

Оператор «и» используется для объединения двух условий, при которых оба должны быть истинными, чтобы получить истинный результат. Например, мы можем использовать оператор «и» для нахождения чисел, которые одновременно являются четными и положительными.

Оператор «в» используется для установления связи между элементами и множествами. Например, мы можем использовать оператор «в» для определения, принадлежит ли число определенному множеству. Например, мы можем проверить, принадлежит ли число 5 множеству простых чисел.

Практическое применение операторов «и» и «в» в решении задач позволяет нам легче определить требования и условия задачи, а также логически связать различные элементы для получения точного результата.

Пример:

Предположим, что нам нужно найти все числа от 1 до 10, которые одновременно являются четными и положительными.

Мы можем использовать оператор «и», чтобы установить, что число должно быть четным и положительным:

Число % 2 == 0 и Число > 0

Теперь мы можем пройти в цикле от 1 до 10 и проверить каждое число на соответствие этому условию:

for (int i = 1; i 0) {
// число i удовлетворяет условию
// выполнение нужных действий
}
}

В результате, в этом примере, мы найдем числа 2, 4, 6 и 8, которые соответствуют обоим условиям — они четные и положительные.

Таким образом, практическое применение операторов «и» и «в» в решении задач помогает нам более точно определить условия и требования задачи, а также эффективно фильтровать и обрабатывать данные.

Вопрос-ответ:

Зачем в математике используются символы «и» и «в»?

Символ «и» в математике используется для объединения двух условий. Символ «в» обозначает принадлежность элемента к множеству.

Можете дать пример использования символа «и»?

Конечно! Например, если у нас есть два условия: «x > 0» и «x < 10», то их объединение будет выглядеть так: «0 < x < 10».

Каким образом символ «в» используется для обозначения принадлежности к множеству?

Символ «в» ставится между элементом и множеством, к которому он принадлежит. Например, если x — элемент множества A, то это записывается как «x в A».

Можете привести пример использования символа «в»?

Конечно! Предположим, что у нас есть множество A, состоящее из чисел {1, 2, 3}. Если x = 2, то мы можем записать это как «2 в A», что означает, что число 2 принадлежит множеству A.

Могут ли символы «и» и «в» использоваться вместе?

Да, символы «и» и «в» могут использоваться вместе. Например, если у нас есть два условия: «x > 0» и «x в A», мы можем объединить их с помощью символа «и» и записать как «x > 0 и x в A». Это означает, что число x больше нуля и принадлежит множеству A.

Что означают символы «и» и «в» в математике?

В математике символ «и» обозначает логическую операцию «И». Она выполняется только тогда, когда оба утверждения истинны. Символ «в» в математике обозначает принадлежность элемента множеству. Например, «х в А» означает, что элемент «х» принадлежит множеству «А».

Как использовать символ «и» в математике?

Символ «и» используется для объединения двух утверждений и обозначает их одновременное выполнение. Например, если у нас есть утверждение «А > 0» и утверждение «В < 5», то мы можем их объединить с помощью символа «и»: «А > 0 и В < 5». Такое объединение будет истинным только в том случае, если оба утверждения истинны.

Понятие «и» и «в» в других областях науки

Понятия «и» и «в» также широко используются в других областях науки, помимо математики. Например, в логике и философии, они играют важную роль для определения отношений и связей между объектами и понятиями.

В логике, союз «и» используется для объединения двух или более высказываний. Высказывание, состоящее из нескольких частей, с союзом «и» будет считаться истинным только в случае, если все его части истинны. Например, если высказывание «Солнце светит» и «Небо голубое» являются истинными, то высказывание «Солнце светит и небо голубое» также будет истинным.

В философии, союз «и» используется для объединения понятий, их атрибутов или свойств. Например, в выражении «Человек разумный и добрый», союз «и» указывает на то, что человек обладает обоими указанными качествами одновременно. Таким образом, «и» позволяет объединять понятия и описывать сложные связи между ними.

Союз «в» также имеет свои отличительные значения в различных областях науки. Например, в физике, он используется для обозначения векторов, которые представляют силы, скорости или перемещения. Вектор «в» может быть направлен в определенном направлении и иметь определенную величину.

В геометрии, союз «в» используется для указания принадлежности точки к определенной фигуре или множеству. Например, точка «А» находится «в» окружности «О», что означает, что точка «А» принадлежит окружности «О».

Таким образом, понятия «и» и «в» имеют широкое применение в различных областях науки, где они используются для объединения, определения отношений и указания принадлежности.

Видео по теме: