Символ который в математике часто употребляют для обозначения суммы
Содержимое
- 1 Символ который в математике часто употребляют для обозначения суммы
- 1.1 Определение и назначение символа суммы
- 1.2 История символа суммы
- 1.3 Значение символа суммы в математических выражениях
- 1.4 Применение символа суммы в арифметике
- 1.5 Применение символа суммы в алгебре
- 1.6 Применение символа суммы в геометрии
- 1.7 Видео по теме:
- 1.8 Вопрос-ответ:
- 1.9 Применение символа суммы в теории вероятностей
- 1.10 Применение символа суммы в физике
Символ суммы в математике используется для обозначения операции сложения и суммы ряда. Узнайте, как использовать этот символ и его особенности.
Математика – одна из самых фундаментальных и точных наук, которая занимается изучением чисел, структур и пространств. В процессе изучения математики мы сталкиваемся с различными символами и обозначениями, которые помогают нам упростить вычисления и описать сложные математические концепции. Один из таких символов – символ суммы.
Символ суммы представляет собой большую греческую букву Сигма (Σ) и используется для обозначения суммы ряда чисел или выражений. Он позволяет нам компактно записывать и вычислять сумму большого количества слагаемых. Например, с помощью символа суммы мы можем записать и вычислить сумму всех натуральных чисел от 1 до 100:
∑i = 1^100 i
Эта запись означает, что мы суммируем все числа (i) от 1 до 100. Символ суммы облегчает запись и позволяет нам выполнять вычисления более эффективно.
Определение и назначение символа суммы

Символ суммы в математике представляет собой знак, который используется для обозначения операции суммирования. Он представляет собой границы суммирования, например, нижнюю и верхнюю границы индексов.
Символ суммы имеет следующий вид: ∑. Он состоит из заглавной греческой буквы сигма (Σ), которая обозначает сумму, и индексов, которые указывают, какие значения нужно просуммировать.
Назначение символа суммы заключается в том, чтобы обозначать операцию суммирования в математических выражениях. Он позволяет удобно записывать суммы большого количества слагаемых, особенно когда количество слагаемых зависит от переменной.
Символ суммы обладает рядом свойств и правил, которые позволяют упростить вычисления и анализировать суммы. Например, он позволяет менять порядок суммирования, разбивать сумму на несколько частей и выносить константы за знак суммы.
Символ суммы широко используется в различных областях математики, физики и других науках. Он является одним из базовых символов и инструментов для работы с суммами и рядами.
История символа суммы
Символ суммы, обозначаемый большой греческой буквой сигма Σ, используется в математике для обозначения операции сложения нескольких чисел или элементов. Этот символ имеет богатую историю и широкое применение в различных областях математики.
Первоначально символ суммы был предложен и использован Леонардом Эйлером, выдающимся математиком XVIII века. Эйлер применил этот символ в своих работах и статьях, чтобы обозначить суммы рядов или последовательностей чисел. Он выбрал символ сигмы, потому что она является первой буквой слова «сумма» на греческом языке.
Впоследствии символ суммы был широко принят в научном сообществе и стал стандартным обозначением операции сложения. Он использовался в различных областях математики, включая алгебру, теорию вероятностей, анализ и комбинаторику. Символ суммы также нашел свое применение в физике, инженерии и других науках.
Символ суммы обычно используется в следующей форме:
| Σ | k=a | n | f(k) |
Здесь k — переменная, a — нижний предел суммирования, n — верхний предел суммирования, а f(k) — функция, определенная для каждого значения k от a до n. Символ суммы позволяет собрать все значения функции f(k) для всех значений переменной k и получить общую сумму.
Использование символа суммы позволяет компактно и ясно записывать сложные математические выражения, а также упрощает исследование и анализ сумм рядов и последовательностей чисел. Благодаря своей универсальности и понятности, символ суммы стал неотъемлемой частью математической нотации и используется во множестве разных контекстов.
Значение символа суммы в математических выражениях
Символ суммы в математике, обозначаемый знаком Σ, используется для записи суммы ряда чисел или выражений. Этот символ позволяет компактно и удобно записывать выражения, в которых требуется сложить большое количество чисел.
Знак Σ часто используется в контексте обозначения суммы от заданного начального значения до заданного конечного значения переменной. Например, сумма чисел от 1 до 5 может быть записана как Σ i=1^5 i. Здесь i — переменная, которая принимает значения от 1 до 5, а сумма обозначается символом Σ.
Значение символа суммы в математических выражениях представляет собой сумму всех чисел или выражений, которые указаны после знака Σ. Например, сумма чисел от 1 до 5 будет равна 15.
Символ суммы широко используется в различных областях математики, физики и информатики. Он позволяет компактно записывать сложные выражения и упрощает работу с большими объемами данных. С помощью символа Σ можно вычислять суммы чисел, выражений и рядов, а также применять его в различных математических и статистических формулах.
ПримерЗначение
| Σ i=1^5 i | 15 |
| Σ n=0^∞ 2^n | бесконечность |
| Σ k=1^n k^2 | Σ k=1^1 k^2 + Σ k=2^2 k^2 + … + Σ k=n^n k^2 |
Применение символа суммы в арифметике
Символ суммы (∑) широко используется в арифметике для обозначения суммы ряда чисел или выражений. Он позволяет компактно записывать большие суммы и облегчает работу с ними.
Применение символа суммы в арифметике может быть разнообразным:
1. Суммирование числовых рядов:
Символ суммы позволяет компактно записывать суммы чисел, находящихся в определенном порядке. Например, сумма первых 10 натуральных чисел:
∑ i = 1 to 10 i = 1 + 2 + 3 + … + 10 = 55
2. Суммирование выражений:
Символ суммы также применяется для суммирования выражений, включающих переменные и функции. Например, сумма квадратов первых n натуральных чисел:
∑ i = 1 to n i^2 = 1^2 + 2^2 + 3^2 + … + n^2
3. Вычисление суммы с определенными условиями:
Символ суммы позволяет вычислять суммы только тех элементов ряда, которые удовлетворяют определенным условиям. Например, сумма только нечетных чисел:
∑ i = 1 to 10 (2i — 1) = (2*1 — 1) + (2*2 — 1) + … + (2*5 — 1) = 25
Применение символа суммы в арифметике позволяет сократить объем записи и упростить вычисления. Он является важным инструментом для работы с суммами и рядами в математике и науке.
Применение символа суммы в алгебре
Символ суммы ∑ используется в алгебре для обозначения суммы нескольких чисел или выражений. Он позволяет удобно записывать и вычислять суммы большого числа слагаемых, упрощая математические выкладки.
В алгебре символ суммы широко применяется для записи и расчета суммы арифметических и геометрических прогрессий, суммы ряда чисел или функций, а также для выражения общего вида формул и закономерностей.
Например, с помощью символа суммы можно записать формулу для суммы первых n членов арифметической прогрессии: ∑ai = a1 + (a1 + d) + (a1 + 2d) + … + (a1 + (n-1)d), где ai — i-й член прогрессии, a1 — первый член прогрессии, d — разность прогрессии, n — количество членов.
Также символ суммы используется для записи суммы ряда чисел или функций, например, ∑an = a1 + a2 + a3 + … + an, где an — n-й член ряда.
Примеры применения символа суммы в алгебреПримерЗначение
| ∑(2k) | Сумма всех четных чисел |
| ∑(3n — 1) | Сумма всех чисел, увеличенных на 1 и умноженных на 3 |
| ∑(2n) | Сумма всех степеней числа 2 |
Применение символа суммы в геометрии

В геометрии символ суммы применяется для обозначения суммы углов в многоугольнике. Допустим, у нас есть многоугольник с n углами. Общая сумма углов этого многоугольника может быть выражена с помощью символа суммы следующим образом:
∑ α = (n — 2) * 180°
Здесь α обозначает каждый угол многоугольника, а n — количество углов. Формула говорит нам, что сумма всех углов многоугольника равна произведению разности количества углов на 2 и 180°.
Применение символа суммы в геометрии не ограничивается только суммой углов в многоугольнике. Он также может использоваться для обозначения суммы длин отрезков, площади фигур и других геометрических параметров.
Использование символа суммы в геометрии позволяет упростить запись формул и выражений, делая их более компактными и понятными.
Таким образом, символ суммы играет важную роль в геометрии, помогая удобно записывать и вычислять суммы углов, длин отрезков и других геометрических параметров.
Видео по теме:
Вопрос-ответ:
Каково значение символа суммы в математике?
Символ суммы в математике используется для обозначения операции сложения последовательности чисел или выражений. Он позволяет сократить запись и упростить вычисления.
Как правильно использовать символ суммы?
Символ суммы обычно записывается в виде большой греческой буквы «сигма» (∑) с индексами над и под ней. Индексы указывают на начало и конец суммирования, а выражение под символом суммы определяет, что именно нужно складывать.
Какие примеры применения символа суммы в математике?
Символ суммы широко используется в различных областях математики. Например, он применяется для вычисления суммы арифметической или геометрической прогрессии, для нахождения суммы ряда или для подсчета площади под графиком функции.
Какие свойства имеет символ суммы?
Символ суммы обладает несколькими важными свойствами. Например, он линеен, то есть можно вынести константу за знак суммы. Также символ суммы можно применять к суммам внутри суммы, что позволяет сократить запись и упростить вычисления.
Можно ли использовать символ суммы для других операций, кроме сложения?
Символ суммы применяется исключительно для обозначения сложения и не может быть использован для других операций, таких как вычитание, умножение или деление.
Применение символа суммы в теории вероятностей

Символ суммы в математике широко применяется в теории вероятностей. Он используется для обозначения суммы вероятностей событий.
Вероятность – это числовая характеристика события, которая показывает, насколько вероятно его наступление. Сумма вероятностей двух или более несовместных событий равна вероятности их объединения.
Таким образом, символ суммы позволяет нам удобно записывать вероятности объединения нескольких событий. Например, если есть события A, B и C, то сумма вероятностей их объединения может быть записана как P(A ∪ B ∪ C) = P(A) + P(B) + P(C).
Этот символ также может использоваться для записи вероятности суммы случайных величин. Например, если X и Y – независимые случайные величины, то вероятность того, что их сумма будет равна определенному значению k, может быть выражена как P(X + Y = k) = ∑ P(X = i) P(Y = k — i), где символ суммы обозначает суммирование по всем возможным значениям i.
Символ суммы в теории вероятностей также может использоваться для нахождения математического ожидания случайной величины. Математическое ожидание – это среднее значение случайной величины, которое она принимает с учетом их вероятностей. Например, если X – случайная величина, принимающая значения x1, x2, …, xn с вероятностями p1, p2, …, pn соответственно, то математическое ожидание X может быть выражено как E(X) = ∑ xi pi.
ПримерВероятность
| X = 0 | 0.2 |
| X = 1 | 0.3 |
| X = 2 | 0.5 |
В данном примере, математическое ожидание X будет равно E(X) = 0 * 0.2 + 1 * 0.3 + 2 * 0.5 = 1.3.
Таким образом, символ суммы играет важную роль в теории вероятностей, позволяя удобно записывать и решать различные задачи, связанные с вероятностями событий и случайными величинами.
Применение символа суммы в физике
Символ суммы, обозначаемый знаком Σ, широко используется в физике для обозначения суммирования значений величин.
В физике символ суммы позволяет суммировать значения физических величин, которые могут меняться в зависимости от определенной переменной. Например, для описания траектории движения тела можно использовать символ суммы для суммирования всех малых перемещений, чтобы получить полное перемещение.
Также символ суммы широко применяется в физике для суммирования значений сил, моментов, энергий и других величин. Например, при расчете работы, выполненной над системой, можно использовать символ суммы для суммирования всех малых приращений работы.
Применение символа суммы в физике позволяет упростить запись и анализ различных физических процессов и явлений, делая их более компактными и наглядными.

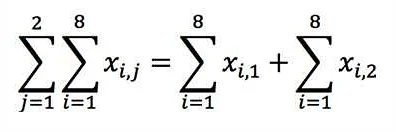



Статья очень понятно и подробно объясняет значение и применение символа суммы в математике. Я всегда интересовался этой темой, и теперь у меня наконец-то есть ясность. Символ суммы ∑ позволяет нам быстро и эффективно вычислять суммы большого количества чисел. Это очень полезно, например, при работе с большими массивами данных или при анализе статистики. Теперь я точно знаю, как использовать этот символ и как с его помощью решать сложные задачи. Большое спасибо автору за интересную и познавательную статью! Буду рекомендовать ее своим друзьям, которые тоже увлекаются математикой.