Что значит целые числа в математике
Содержимое
- 1 Что значит целые числа в математике
Целые числа в математике — это числа, которые не содержат дробной части или десятичных знаков. Они включают в себя положительные и отрицательные числа, а также ноль. Целые числа используются для решения задач, связанных с подсчетом, измерениями и манипуляциями с количеством. Они являются одним из основных типов чисел в математике и широко применяются в различных областях науки и повседневной жизни.
Целые числа являются одним из основных понятий в математике. Они включают в себя все натуральные числа, их отрицания и нуль. Таким образом, целыми числами являются все числа, которые можно записать без десятичных дробей и десятичных разделителей.
Целые числа обозначаются символом Z и могут быть положительными, отрицательными или нулем. Это важно помнить, так как целые числа включают в себя и отрицательные значения, которые могут быть использованы для обозначения долгов, убытков и других отрицательных величин.
Например, -3, -2, -1, 0, 1, 2, 3 — все это являются целыми числами. Они могут быть представлены на числовой прямой, где положительные числа находятся справа от нуля, отрицательные числа — слева от нуля, а ноль — сам по себе.
Целые числа часто используются для решения математических задач, моделирования физических процессов и анализа данных. Они важны для понимания более сложных математических концепций, таких как рациональные и иррациональные числа, и играют важную роль в алгебре, геометрии, физике и других науках.
Что такое целые числа в математике?
Целые числа можно представить на числовой прямой, где положительные числа находятся справа от нуля, отрицательные числа — слева, а ноль — в центре. Например:
… -3, -2, -1, 0, 1, 2, 3, …
Целые числа используются в математике для решения широкого спектра задач, таких как алгебраические вычисления, графики, анализ данных и другие.
Определение целых чисел
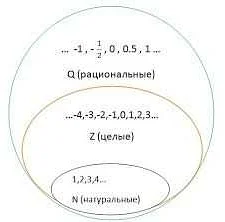
Примеры целых чисел:
- 0 – ноль;
- 1 – натуральное число;
- -1 – отрицательное число;
- 2 – натуральное число;
- -2 – отрицательное число;
- 3 – натуральное число;
- -3 – отрицательное число;
Целые числа позволяют нам решать широкий спектр задач, включая вычисления, алгебру, геометрию и другие области математики.
Примеры целых чисел

На числовой оси целые числа отображаются в виде точек, расположенных на равных расстояниях друг от друга. Например, точка 0 на числовой оси соответствует нулю, точка 1 — единице, точка -1 — минус единице и так далее.
Целые числа используются в различных областях математики и естественных науках для описания целых величин, например, количества объектов, времени, температуры и т.д.
Некоторые другие примеры целых чисел:
- 7
- -10
- 42
- -99
- 0
Это лишь некоторые примеры целых чисел, их бесконечное множество позволяет описывать разнообразные значения и свойства в различных областях математики и наук.
Свойства целых чисел
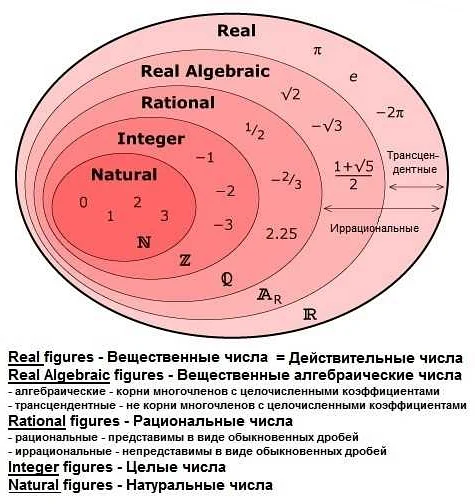
Целые числа имеют некоторые особенности и свойства, которые делают их уникальными в математике.
СвойствоОписаниеПример
| Закон замены | Для любых целых чисел a, b и c, если a = b, то a + c = b + c и a — c = b — c. | Если a = 5, b = 5 и c = 2, то 5 + 2 = 5 + 2 и 5 — 2 = 5 — 2. |
| Ассоциативность сложения и умножения | Для любых целых чисел a, b и c, (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c). | Если a = 2, b = 3 и c = 4, то (2 + 3) + 4 = 2 + (3 + 4) и (2 * 3) * 4 = 2 * (3 * 4). |
| Коммутативность сложения и умножения | Для любых целых чисел a и b, a + b = b + a и a * b = b * a. | Если a = 2 и b = 3, то 2 + 3 = 3 + 2 и 2 * 3 = 3 * 2. |
| Существование нейтральных элементов | Для любого целого числа a, a + 0 = a и a * 1 = a. | Если a = 7, то 7 + 0 = 7 и 7 * 1 = 7. |
| Свойство обратных элементов | Для любого целого числа a, существует целое число -a, такое что a + (-a) = 0. | Если a = 4, то 4 + (-4) = 0. |
| Дистрибутивность умножения относительно сложения | Для любых целых чисел a, b и c, a * (b + c) = (a * b) + (a * c). | Если a = 2, b = 3 и c = 4, то 2 * (3 + 4) = (2 * 3) + (2 * 4). |
Эти свойства помогают в вычислениях и решении математических задач с использованием целых чисел.
Операции с целыми числами
Целые числа подразумевают положительные и отрицательные числа, а также ноль. В математике существует несколько операций, которые можно выполнять с целыми числами:
- Сложение. Целые числа можно складывать, чтобы получить новое число. Например, -3 + 5 = 2.
- Вычитание. Целое число можно вычесть из другого целого числа. Например, 8 — 4 = 4.
- Умножение. Целые числа можно умножать, чтобы получить новое число. Например, -2 * 6 = -12.
- Деление. Целое число можно разделить на другое целое число. Например, 15 / 3 = 5.
- Возведение в степень. Целое число можно возвести в степень, чтобы получить новое число. Например, 2^3 = 8.
- Остаток от деления. Операция возвращает остаток от деления одного целого числа на другое целое число. Например, 10 % 3 = 1.
Эти операции являются основными для работы с целыми числами и позволяют выполнять различные вычисления и решать задачи в математике.
Целые числа на числовой прямой
На числовой прямой целые числа представлены с помощью точек, расположенных на оси. Каждая точка соответствует определенному целому числу, а расстояние между двумя соседними точками равно 1. Ноль обычно помещается в центре числовой прямой, а положительные целые числа располагаются справа от нуля, а отрицательные — слева.
Например, на числовой прямой целые числа от -3 до 3 будут представлены следующим образом:
-3 -2 -1 0 1 2 3
| | | | | | |
————————-
Как видно из примера, каждое целое число имеет свое место на числовой прямой, и они расположены в порядке возрастания или убывания. Числовая прямая помогает визуализировать отношения между целыми числами и выполнять операции с ними, такие как сложение и вычитание.
Применение целых чисел в реальной жизни
Целые числа широко применяются в различных сферах жизни. Ниже приведены несколько примеров:
| Сфера | Пример применения |
| Финансы | Расчеты бухгалтерии, бюджетирование, учет долгов и кредитов |
| Строительство | Измерение и расчеты размеров, объемов материалов, распределение ресурсов |
| Транспорт | Расчеты скорости, расстояний, времени в пути, расхода топлива |
| Торговля | Учет товаров, продажи, рассчеты скидок и налогов |
| Наука и технологии | Моделирование, вычисления, программирование, шифрование |
| Спорт | Расчеты результатов, замеры и анализ физических показателей |
Это лишь несколько примеров применения целых чисел, их использование на самом деле намного шире. В математике целые числа играют важную роль и используются в различных сферах нашей жизни для решения разнообразных задач и вычислений.
Вопрос-ответ:
Что такое целые числа в математике?
Целые числа в математике — это числа, которые включают в себя все натуральные числа, нуль и их отрицательные значения.
Можете ли вы дать определение целых чисел в математике?
Конечные или бесконечные числовые значения, которые включают в себя все натуральные числа, нуль и отрицательные значения, называются целыми числами.
Какие примеры целых чисел можно привести?
Примеры целых чисел: -3, -2, -1, 0, 1, 2, 3 и так далее.
Какие числа не являются целыми числами?
Дробные числа, такие как 1/2, 3/4 или 2.5, не являются целыми числами. Также иррациональные числа, например, корень из 2, также не являются целыми.
В чем отличие целых чисел от натуральных чисел?
Отличие между целыми числами и натуральными числами заключается в том, что натуральные числа включают только положительные числа, начиная с 1, а целые числа включают в себя как положительные, так и отрицательные значения, а также ноль.
Целые числа в компьютерных науках
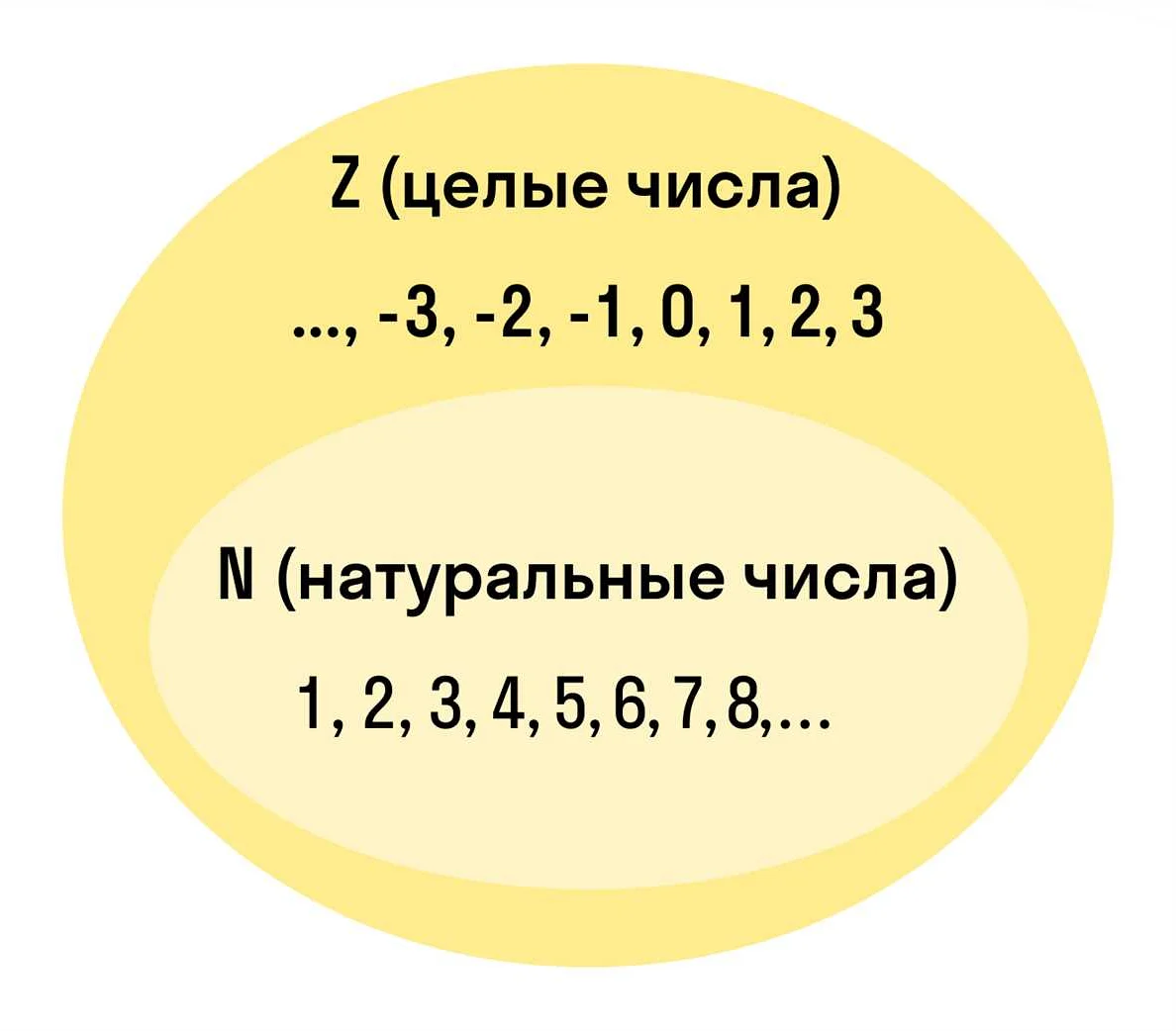
В компьютерных науках целые числа обычно представляются с помощью битовых последовательностей. Размер целого числа определяется количеством битов, выделенных для его представления. Наиболее распространены целые числа, представленные 8, 16, 32 или 64 битами.
Целые числа в компьютерных науках могут использоваться для различных целей, включая счетчики, индексы массивов, флаги и т.д. Они могут быть операндами математических операций, логических операций и операций сравнения.
Примеры целых чисел в компьютерных науках:
Тип данныхОписаниеПример
| int | Целое число со знаком | -10, 0, 5 |
| unsigned int | Целое число без знака | 0, 10, 255 |
| long | Длинное целое число со знаком | -1000000, 0, 1000000 |
| unsigned long | Длинное целое число без знака | 0, 1000000, 4294967295 |
Целые числа в компьютерных науках являются важным элементом при разработке программ и алгоритмов. Они позволяют выполнять различные вычисления и манипуляции с данными, что делает их неотъемлемой частью компьютерных наук.



Очень интересная статья! Математика всегда вызывала у меня некоторое волнение, но я стараюсь разбираться в этой науке. Понятие «целые числа» — это такой фундаментальный элемент, который часто используется в различных математических операциях. Целые числа включают в себя все натуральные числа, а также их отрицательные значения и ноль. Это позволяет нам работать с числами в любом направлении, не ограничиваясь только положительными значениями. Примеры целых чисел можно найти везде вокруг нас: от температуры за окном до количества банок в супермаркете. Если мы говорим о количестве чего-либо, которое может быть как положительным, так и отрицательным, то мы говорим о целых числах. Например, если у нас есть 5 яблок и мы съедаем 3 из них, у нас остаётся 2 яблока. В данном случае мы используем положительные целые числа. Но если у нас было 2 яблока, а мы съели 3, то у нас будет -1 яблоко. Это уже отрицательное целое число. Целые числа также широко применяются в алгебре, геометрии и других математических дисциплинах. Они помогают нам решать сложные уравнения, находить корни и решать задачи. Без понимания и умения работать с целыми числами было бы очень сложно разбираться во многих математических концепциях. В целом, понятие «целые числа» играет важную роль в математике, а также нашей повседневной жизни. Оно помогает нам понимать и описывать мир вокруг нас через числа и операции над ними. Благодаря целым числам, мы можем анализировать и понимать различные ситуации и явления, и использовать их для наших потребностей.
Математика, это то, что меня всегда увлекало и интересовало. Я всегда стремился понять основные концепции и понятия этой науки, и одним из таких понятий являются целые числа. Целые числа — это числа, которые можно представить в виде натуральных чисел, их противоположностей (отрицательных чисел) и нуля. Они получаются путем комбинирования положительных и отрицательных чисел, и включают в себя все натуральные числа, а также числа с минусом. Примеры целых чисел можно найти в разных ситуациях. Например, если я стою на одном конце числовой оси и двигаюсь влево, я буду проходить через все отрицательные целые числа: -1, -2, -3 и так далее. Если же я двигаюсь вправо, я буду проходить через все положительные целые числа: 1, 2, 3 и так далее. И наконец, когда я останавливаюсь на точке ноль, я достигаю нулевого значения, которое также является целым числом. Целые числа играют важную роль в математике и в реальном мире. Они помогают нам сравнивать и упорядочивать числа, а также представлять отрицательные значения. Кроме того, целые числа широко используются в алгебре, геометрии, физике и других науках. В заключение, целые числа — это важное понятие в математике, которое помогает нам понять и описывать мир вокруг нас. Они представляют собой комбинацию положительных и отрицательных чисел, а также нуля, и находят применение в различных областях знаний.