Натуральные числа в математике: что это такое?

Натуральное число в математике обозначает количество элементов в конечном множестве. Оно используется для счета, измерения и определения порядка. Узнайте подробнее о свойствах натуральных чисел и их роли в математике.

Натуральное число является основным понятием в математике и используется повсеместно, начиная с элементарной алгебры и заканчивая более сложными математическими теориями. Определение натурального числа относится к естественным числам, которые являются неотрицательными и целыми числами, используемыми для подсчета количества предметов и измерения их количественных характеристик.

Концепция натуральных чисел и их свойств имеет центральное значение в математике. Они обладают множеством важных характеристик, которые рассматриваются в различных областях математики, включая теорию чисел, комбинаторику, геометрию, математическую анализ и абстрактную алгебру.

В этой статье мы рассмотрим основные свойства натуральных чисел и какие законы лежат в основе их определения. Мы также рассмотрим применение натуральных чисел в различных областях математики и их значение в повседневной жизни.

Что такое натуральное число?

Натуральное число – это целое положительное число, которое используется в математике для обозначения количества объектов в некотором множестве. Это могут быть люди, яблоки, дни недели, и т.д. Натуральные числа представлены следующей последовательностью: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и так далее.

Наибольшим преимуществом натуральных чисел является то, что они обладают свойством порядка, то есть каждое натуральное число следует за предыдущим. Это свойство помогает упорядочивать различные объекты и процессы, и использовать математические операции для решения различных задач.

Также натуральные числа обладают свойством ассоциативности, то есть результат операции сложения или умножения натуральных чисел не зависит от порядка выполнения операций. Например, 3 + (4 + 5) = (3 + 4) + 5 = 12.

Натуральные числа являются основой для описания многих математических концепций и теорий, и используются в широком спектре научных и инженерных приложений, таких как статистика, теория вероятности, компьютерные науки и т.д.

Видео по теме:

Определение натурального числа в математике

Натуральное число – это число, используемое для подсчета количества объектов. Натуральные числа образуются последовательной нумерацией объектов, начиная с 1. Таким образом, каждому объекту соответствует свое натуральное число. Также натуральные числа могут использоваться для представления временных промежутков, расстояний и т. д.

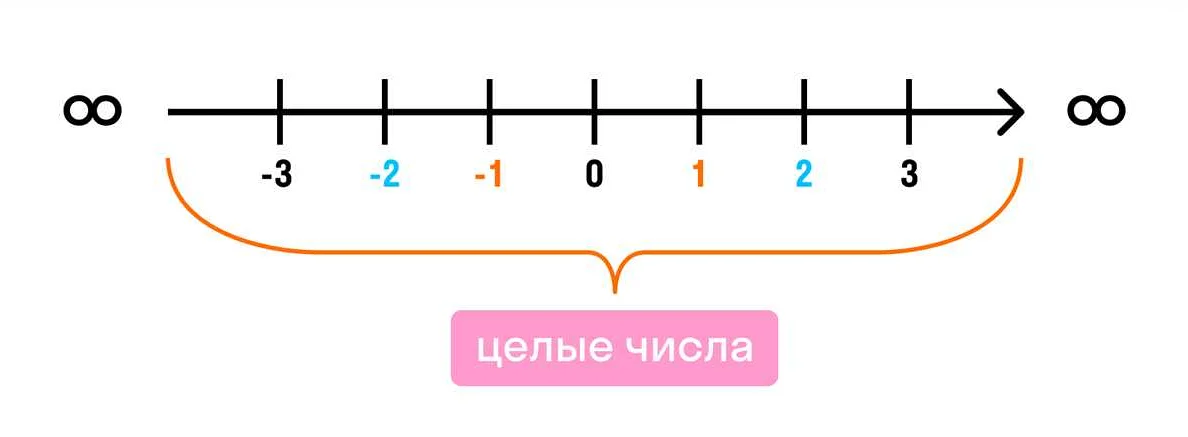
Натуральные числа обозначаются символом N и могут быть записаны как 1, 2, 3… и так далее до бесконечности. Кроме того, множество натуральных чисел N является бесконечным и неограниченным в обе стороны. Это означает, что в любой момент времени можно найти натуральное число, большее любого заданного числа.

Натуральные числа обладают несколькими важными свойствами, в том числе свойством ассоциативности, коммутативности и дистрибутивности. Ассоциативность означает, что порядок выполнения операций не влияет на результат. Коммутативность подразумевает, что порядок слагаемых в сумме или множителей в произведении не влияет на результат. Дистрибутивность же применима при выполнении операций сложения и умножения.

Таким образом, натуральные числа являются базовым строительным блоком в математике и используются в широком диапазоне задач и приложений, начиная с простых задач по счету и заканчивая сложными вопросами в физике, науке и экономике.

Символизация натурального числа

Натуральные числа можно символизировать с помощью цифр от 0 до 9. Для записи больших чисел можно использовать многоразрядную систему счисления. При этом старший разряд отображает количество степеней десяти, которые нужно умножить на натуральное число, второй – количество степеней десяти, которые нужно умножить на 10, и т. д.

Натуральные числа могут быть записаны и в текстовой форме. В таком случае, используются словесные обозначения цифр: один, два, три, и так далее. Кроме того, существует международная стандартная запись длинных чисел, в которой применяются триллионы, биллионы, миллиарды и так далее.

• Примеры в текстовой форме: 389 – триста восемьдесят девять, 1203 – одна тысяча двести три.
• Примеры в международной стандартной записи: 1 000 000 – один миллион, 10 000 000 – десять миллионов, 1 000 000 000 – один миллиард, 1 000 000 000 000 – один триллион.

ЦифрыЗначение

0	Ноль
1	Один
2	Два
3	Три
4	Четыре
5	Пять
6	Шесть
7	Семь
8	Восемь
9	Девять

Необходимо заметить, что одно и то же число может быть записано несколькими способами: цифрами, словами, международной стандартной записью и т.д. Также есть некоторые правила записи чисел на языке, поэтому следует учитывать их, чтобы избежать ошибок.

Структура натурального числа

Натуральное число — это число, которое служит для обозначения количества предметов.

В состав натурального числа входят:

• Цифры от 0 до 9;
• Разряды (единицы, десятки, сотни и т.д.);

Например, число 153 состоит из трех разрядов: сотен (1), десятков (5) и единиц (3).

В натуральных числах также присутствуют следующие свойства:

1. Непрерывность: между любыми двумя натуральными числами существует бесконечное количество других натуральных чисел.
2. Упорядоченность: натуральные числа упорядочены по возрастанию.
3. Аддитивность: при прибавлении к одному натуральному числу другого получается новое натуральное число.
4. Мультипликативность: при умножении одного натурального числа на другое получается новое натуральное число.

Таким образом, структура натурального числа представляет собой цифры, разряды и свойства, такие как непрерывность, упорядоченность, аддитивность и мультипликативность.

Основные свойства натуральных чисел

Натуральные числа – это числа, которые можно использовать для подсчёта предметов или явлений в окружающем мире.

Основные свойства натуральных чисел:

• Положительность: натуральные числа всегда больше или равны нулю.
• Порядок: натуральные числа упорядочены по возрастанию. Например, 1 < 2 < 3.
• Сложение и умножение: натуральные числа можно складывать и умножать между собой, и результатом такой операции будет тоже натуральное число.
• Разложение на множители: каждое натуральное число можно представить в виде произведения простых чисел.
• Делители: каждое натуральное число имеет свой набор делителей. Например, делителями числа 6 являются 1, 2, 3 и 6.

Натуральные числа являются одними из основных элементов математики и широко используются во многих областях, в том числе в физике, экономике и информатике.

Натуральные числа являются положительными

Натуральные числа – это числа, которые используются для подсчета единиц товара, населения и других количественных характеристик. К ним относятся числа 1, 2, 3, 4, 5 и так далее. Одно из основных свойств натуральных чисел заключается в том, что они всегда положительны. Это значит, что они не принимают отрицательных значений.

Кроме того, натуральные числа не могут быть дробями или десятичными числами. Например, число 1.5 не является натуральным числом, потому что оно имеет дробную часть. Это требование, что натуральные числа должны быть целыми, делает их особенно полезными для математических вычислений и приложений, связанных с количественными анализом данных.

Натуральные числа используются во многих областях, включая математику, физику, экономику и компьютерные науки. Они представляют собой базис для различных математических операций, а также для различных типов алгебраических и геометрических объектов. По этой причине они являются одними из самых важных числовых концепций во всяком учебном курсе по математике.

В целом, положительность натуральных чисел является важной характеристикой в их свойствах и определении. Она позволяет использовать их во множестве задач и прикладных приложений, включая алгебраические и геометрические расчеты, анализ данных и прогнозирование.

Натуральные числа не содержат дробей

Натуральные числа — это числа, которые применяются для подсчетов количества объектов или событий. Они начинаются с числа 1 и не имеют никаких дробных или отрицательных значений.

Это значит, что любое натуральное число можно представить в виде суммы 1 + 1 + 1… , где каждый слагаемый равен единице, и такое представление единственно.

Из-за отсутствия дробей в натуральных числах мы не можем использовать их для подсчетов чего-либо, что не является целочисленным количеством объектов или событий.

Например, если у нас есть 5 яблок, мы можем использовать натуральное число 5 для подсчета их количества. Однако, если у нас есть половина яблока, мы не можем использовать натуральные числа для подсчета, так как они не содержат дробей.

Таким образом, понимание того, что натуральные числа не содержат дробей, очень важно в математике, особенно в элементарной арифметике.

Натуральные числа не могут быть отрицательными

В математике натуральные числа обозначаются символом N и включают в себя все положительные целые числа, начиная с единицы (1), 2, 3 и т.д.

Важным свойством натуральных чисел является то, что они не могут быть отрицательными. Например, число -3 не может быть натуральным, так как оно отрицательное.

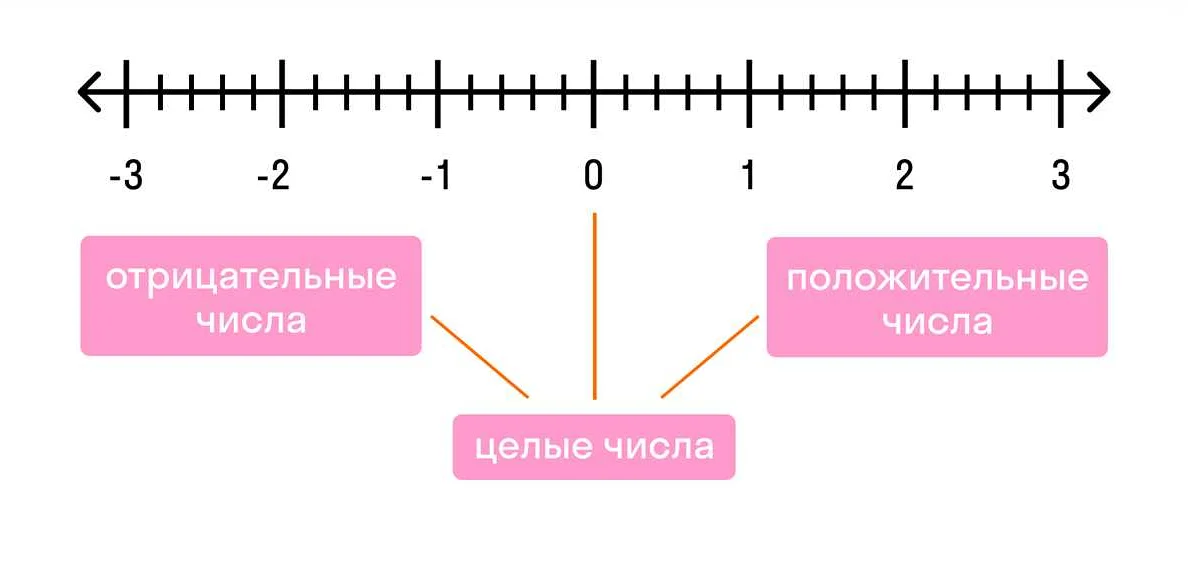
Отрицательные числа, включая целые числа (например, -1, -2, -3), входят в другое множество — множество целых чисел (обозначается символом Z). Множество целых чисел включает в себя натуральные числа, а также отрицательные числа и нуль.

Таким образом, натуральные числа — это только положительные целые числа, начиная с 1, и они не могут быть отрицательными. Понимание этого свойства помогает правильно решать задачи по математике, особенно в алгебре и численных методах.

Натуральные числа являются бесконечными

Натуральные числа — это числа, которые используются для подсчета предметов в окружающей нас действительности. Это числа, которые начинаются с единицы и не имеют верхней границы. То есть, нет такого натурального числа, которое было бы последним. Каждое натуральное число можно увеличить на единицу и получить новое натуральное число. Таким образом, натуральные числа — это бесконечный набор чисел.

При работе с натуральными числами в математике очень важно понимать, что их множество бесконечно. Это значит, что нельзя проверить каждое натуральное число, чтобы убедиться в том, что оно действительно является натуральным. Также нельзя перечислить все натуральные числа, потому что они бесконечны.

Бесконечность множества натуральных чисел придает им некоторые особенности и свойства. Например, существует бесконечное количество простых чисел. Одинаковых натуральных чисел тоже не бывает, потому что каждое число отличается от других, даже если только на единицу.

Изначально множество натуральных чисел было создано для описания количества объектов или предметов в реальном мире. С течением времени оно получило абстрактный математический смысл и активно используется для решения различных задач в науке, технике и экономике.

Арифметические операции с натуральными числами

Натуральные числа — это числа, которые используются для подсчета предметов в реальном мире, они начинаются с 1 и включают в себя все положительные целые числа. Арифметические операции с натуральными числами включают в себя сложение, вычитание, умножение и деление.

Сложение натуральных чисел происходит путем суммирования двух или более чисел. Например, 2 + 3 = 5. При сложении натуральных чисел, порядок чисел не имеет значения, а результат всегда больше или равен сумме исходных чисел.

Вычитание натуральных чисел происходит путем вычитания одного числа из другого. Например, 8 − 3 = 5. При вычитании натуральных чисел, результат всегда положительный, если первое число больше второго.

Умножение натуральных чисел происходит путем умножения двух или более чисел. Например, 3 × 4 = 12. При умножении натуральных чисел результат всегда положительный, а порядок чисел не имеет значения.

Деление натуральных чисел происходит путем разделения одного числа на другое. Например, 12 ÷ 3 = 4. При делении натуральных чисел, результат может быть целым или дробным числом, а делитель не может быть равен нулю.

Использование арифметических операций может помочь в подсчете и решении проблем в реальном мире, что делает натуральные числа основными элементами в математике и ее приложениях.

Сложение натуральных чисел

Натуральные числа – это числа, которые используются для подсчета предметов или событий. Они начинаются с 1 и увеличиваются на единицу в порядке возрастания. Операция сложения натуральных чисел – это процесс соединения двух или более этих чисел для получения нового числа. Например, если мы сложим 2 и 3, то получим 5.

Сложение двух натуральных чисел происходит в несколько этапов. Мы сначала складываем единицы, затем десятки, сотни и так далее. Если результат сложения превышает 9, то мы переносим единицу на следующий разряд.

Давайте рассмотрим пример: мы хотим сложить 345 и 678. Сначала мы складываем единицы: 5 + 8 = 13. По правилам сложения натуральных чисел, единицу мы записываем под этими цифрами, а единицу переносим на следующий разряд. Тогда результат сложения единиц – 3. Теперь складываем десятки: 4 + 7 + 1 (перенесенная единица) = 12. Записываем два и единицу переносим на следующий разряд. И так далее.

Сложение натуральных чисел имеет свойства ассоциативности, коммутативности и дистрибутивности. Ассоциативность говорит о том, что порядок слагаемых не влияет на результат операции. Коммутативность говорит о том, что порядок слагаемых можно изменять без изменения результата операции. Дистрибутивность говорит о том, что умножение числа на сумму чисел можно представить как сумму произведений чисел.

• Свойство ассоциативности: (а + b) + c = а + (b + c)
• Свойство коммутативности: а + b = b + a
• Свойство дистрибутивности: а(b + c) = ab + ac

Натуральные числа являются важным инструментом в математике, физике, экономике и других науках. Сложение натуральных чисел является основой для более сложных операций, таких как вычитание, умножение и деление.

Вычитание натуральных чисел

Вычитание – это одно из четырех арифметических действий, которые выполняют с натуральными числами. Оно представляет собой операцию нахождения разности между двумя числами – уменьшаемым и вычитаемым.

Чтобы выполнить вычитание, необходимо поставить вычитаемое слева от знака вычитания, а справа – уменьшаемое. Далее вычитаем числа побригадно, начиная с последнего разряда. Если цифры в уменьшаемом больше, чем в вычитаемом, то нужно выполнить заем цифры из вышестоящего разряда, чтобы продолжить вычитание.

Пример вычитанияУменьшаемоеВычитаемоеРазность

5	2	8
1	4	7
4	8	1

Разность между числами может быть при этом как положительной, так и отрицательной. Если результат вычитания положительный, то оно называется вычитанием с переносом, а если отрицательным – вычитанием с заемом. Вычитание с заемом возникает в том случае, когда в уменьшаемом числе отсутствует одна из цифр, необходимая для вычитания. В этом случае занимается из старшего разряда соседнего числа, что влияет на результат операции.

Вычитание натуральных чисел широко используется в математических и физических расчетах, а также в повседневной жизни человека.

Умножение натуральных чисел

Умножение натуральных чисел – это арифметическая операция, результатом которой является произведение. Произведением двух натуральных чисел a и b является число, равное сумме a, складываемой b раз.

Например, произведение 2 и 3 равняется 6, потому что 2 + 2 + 2 = 6. Произведение можно записать в виде a * b, где a и b являются множителями.

Умножение натуральных чисел обладает несколькими свойствами. Одно из них – свойство коммутативности, которое гласит, что результат умножения не зависит от порядка множителей: a * b = b * a.

Другое свойство – свойство ассоциативности, которое означает, что при умножении трех чисел результат получится одинаковый, независимо от того, какие два числа сначала будут умножены: (a * b) * c = a * (b * c).

При умножении больших натуральных чисел, используется столбиковый метод. Каждая цифра второго множителя умножается на все цифры первого множителя, начиная с младшего разряда, а затем результаты складываются. Полученная сумма будет являться произведением двух чисел.

Например, произведение 23 и 54 можно вычислить следующим образом:

		2	3
	*	5	4
———-	———-	———-	———-
		1	2	0
+	1	1	5	2
———-
		1	2	4

Таким образом, 23 умножить на 54 равно 1242.

Деление натуральных чисел

Деление является одной из четырех основных арифметических операций, которую можно произвести с натуральными числами. Она обозначается символом «÷» или «/», и выполняется путем разделения одного числа на другое, которое называется делителем.

При делении натуральных чисел можно выделить два основных понятия: частное и остаток. Частное – это результат деления, т.е. количество раз, которое делитель содержится в делимом. Остаток – это число, которое остается после вычитания из делимого наибольшего кратного делителя.

Деление натуральных чисел имеет некоторые особенности. Наибольшая из них заключается в том, что при делении нацело некоторых чисел, получаются дробные числа. В таком случае мы можем использовать округление вниз или вверх, чтобы получить целое число.

Деление также имеет ряд свойств, связанных с ассоциативностью и дистрибутивностью. Например, ассоциативность означает, что порядок выполнения операций не имеет значения. Дистрибутивность – это свойство, которое позволяет упростить формулы и выражения, сокращая количество операций.

Одним из методов деления является деление в столбик. Он широко используется в начальных классах школы и основывается на разбиении делимого на разряды и расстановке цифр в частном.

В целом, деление является важной операцией не только в математике, но и в повседневной жизни. Она используется в финансовых расчетах, анализе данных, науке и технике, и многих других областях.

Вопрос-ответ:

Что такое натуральное число?

Натуральное число — это положительное целое число, которое используется для определения количества элементов в конечных множествах, например, количество яблок в корзине или количество дней в неделе.

Какие свойства имеют натуральные числа?

Свойства натуральных чисел включают: коммутативность сложения и умножения, ассоциативность сложения и умножения, имеют нейтральные элементы для сложения и умножения, дистрибутивность умножения относительно сложения, каждое натуральное число может быть представлено как произведение простых чисел.

Какие операции можно выполнять с натуральными числами?

Операции, которые можно выполнять с натуральными числами, включают сложение, вычитание, умножение, деление и возведение в степень.

Как проверить, является ли число натуральным?

Чтобы проверить, является ли число натуральным, необходимо убедиться, что оно является положительным целым числом. Если число делится нацело на 1 и на само себя, и не имеет других делителей, то это натуральное число.

Как найти наибольший общий делитель двух натуральных чисел?

Для нахождения наибольшего общего делителя двух натуральных чисел необходимо разложить каждое число на простые множители и найти общие множители. Затем необходимо умножить все общие множители и получить наибольший общий делитель.

Можно ли делить на ноль в натуральных числах?

Нет, нельзя делить на ноль ни в каких числовых системах, в том числе и в системе натуральных чисел. Деление на ноль приводит к неопределенности и противоречиям в математике.

Можно ли использовать натуральные числа для измерения физических величин?

Натуральные числа используются для определения количества элементов в конечных множествах, но они не могут использоваться для измерения физических величин, таких как длина, масса или время. Для измерения таких величин необходимы другие системы измерения, например, метрическая система.