Что означает приставка arc в математике

Pristavka arc в математике является обозначением обратных функций тригонометрии. Узнайте, как использовать приставку arc и как она связана с углами и соответствующими функциями.

Арк — это термин, который часто используется в математике, особенно в геометрии и тригонометрии. Арк представляет собой часть кривой или окружности, ограниченную двумя точками. Эта часть может быть измерена в угловых градусах или в длине.

Когда приставка arc добавляется перед названием геометрической фигуры или функции, она обозначает, что речь идет о какой-то части этой фигуры или функции. Например, arc может быть использован перед названием окружности, чтобы указать на сегмент окружности. Точно так же, arc может быть использован перед названием тригонометрической функции, чтобы указать, что речь идет о арктангенсе или арксекансе.

Например, арктангенс обозначается как arctan, арксеканс как arcsec и так далее.

Использование приставки arc позволяет нам более точно и ясно описывать и обозначать различные части геометрических фигур и функций. Это значительно облегчает математические вычисления и анализ, а также улучшает понимание математических концепций.

Что значит приставка arc в математике: объяснение и примеры

Например, «arcsin» обозначает обратную функцию синуса, «arccos» — обратную функцию косинуса, «arctan» — обратную функцию тангенса и так далее. Эти функции позволяют нам найти угол, значение синуса, косинуса или тангенса которого равно заданному числу.

Например, если синус некоторого угла равен 0,5, то мы можем использовать функцию «arcsin(0,5)», чтобы найти значение этого угла. В данном случае «arcsin(0,5)» вернет значение 30 градусов или π/6 радиан, так как синус 30 градусов равен 0,5.

Также «arc» может обозначать длину дуги окружности. Например, если говорят о «дуге окружности», то это означает часть окружности между двумя точками, а «arc AB» — длину этой дуги.

В общем, приставка «arc» в математике используется для обозначения дуги окружности или обратной функции тригонометрических соотношений, и позволяет нам решать различные задачи связанные с углами и окружностями.

Определение приставки arc в математике

Арксинус (или arcsin) функция определяет угол, у которого синус равен заданному значению. Например, арксинус 0 равен 0, поскольку синус 0 равен 0.

Арккосинус (или arccos) функция определяет угол, у которого косинус равен заданному значению. Например, арккосинус -1/2 равен 2π/3, поскольку косинус 2π/3 равен -1/2.

Арктангенс (или arctan) функция определяет угол, у которого тангенс равен заданному значению. Например, арктангенс 1 равен π/4, поскольку тангенс π/4 равен 1.

Приставка «arc» в математике используется для обозначения обратных тригонометрических функций и помогает определить углы, соответствующие заданным значениям синуса, косинуса и тангенса.

Примеры использования приставки arc в математике

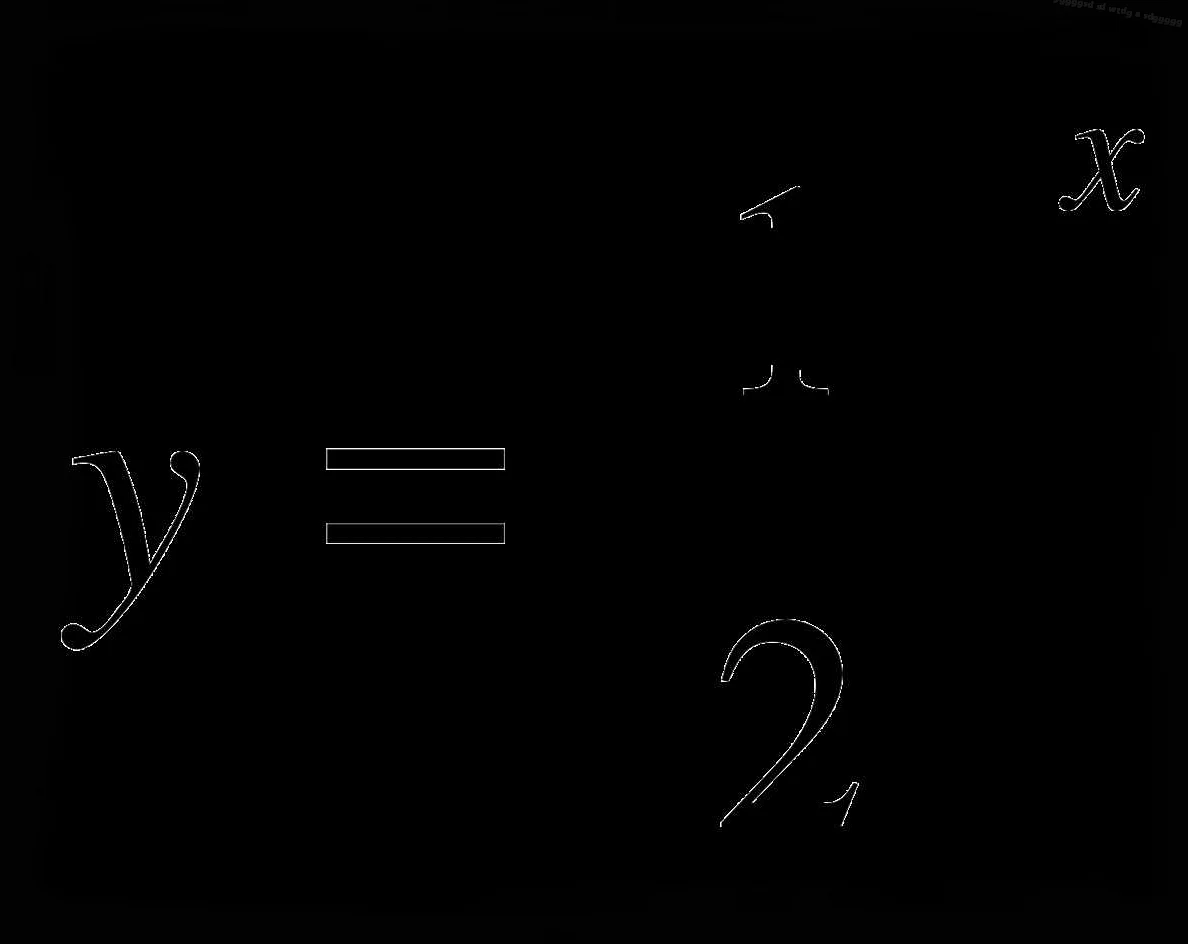
Приставка «arc» в математике часто используется для обозначения арктангенса или арккотангенса. Она указывает на обратную функцию, которая возвращает угол, соответствующий заданному значению тангенса или котангенса.

Например, функция arctan(x) возвращает угол, у которого тангенс равен x. Если x равно 1, то arctan(1) равен 45 градусам.

Таблица ниже показывает значения функций арктангенса и арккотангенса для различных углов:

Угол (в градусах)АрктангенсАрккотангенс

0	0	90
30	0.577	60
45	1	45
60	1.732	30
90	неопределено	0

Таким образом, приставка «arc» позволяет нам вычислять углы, основанные на тангенсе и котангенсе, и использовать их в различных математических операциях и моделях.

Различные значения приставки arc в математике

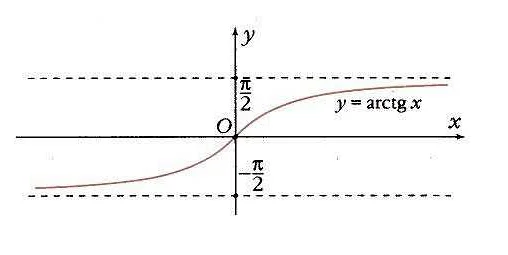
Приставка «arc» в математике используется для обозначения различных понятий и операций. Ниже приведены несколько примеров:

• Арккосинус (arccos): арккосинус числа — это угол, косинус которого равен этому числу. Он обозначается как arccos(x), где x — число от -1 до 1.
• Арксинус (arcsin): арксинус числа — это угол, синус которого равен этому числу. Он обозначается как arcsin(x), где x — число от -1 до 1.
• Арктангенс (arctan): арктангенс числа — это угол, тангенс которого равен этому числу. Он обозначается как arctan(x), где x — любое число.
• Арккотангенс (arccot): арккотангенс числа — это угол, котангенс которого равен этому числу. Он обозначается как arccot(x), где x — любое число.

Приставка «arc» также может использоваться в комбинации с другими словами, чтобы обозначить дугу или дуговую функцию в геометрии или тригонометрии. Например:

• Дуга окружности (arc): в геометрии, дуга окружности — это часть окружности, ограниченная двумя точками.
• Дуговая функция (arc): в тригонометрии, дуговая функция — это функция, определенная на интервале от 0 до π (или от 0 до 2π), которая связывает значения угла и значения тригонометрических функций.

Таким образом, приставка «arc» в математике имеет различные значения и используется для обозначения углов, дуг и дуговых функций.

Приставка arc в геометрии и тригонометрии

Например, функция arcsin(x) возвращает угол, синус которого равен x. Аналогично, arccos(x) возвращает угол, косинус которого равен x, и arctan(x) возвращает угол, тангенс которого равен x. Все эти функции определены только на определенных интервалах и возвращают значения в радианах.

Для удобства использования приставка «arc» часто записывается в виде «asin», «acos» и «atan». Например, asin(x) эквивалентно arcsin(x), и так далее.

Использование приставки «arc» в геометрии и тригонометрии позволяет решать различные задачи, связанные с нахождением углов и сторон треугольников, а также проведением различных геометрических построений.

ФункцияОбозначение

Арксинус	arcsin(x)
Арккосинус	arccos(x)
Арктангенс	arctan(x)

Как использовать приставку arc при измерении углов

Для использования приставки «arc» при измерении углов следует выполнить следующие шаги:

1. Определите центр окружности, вокруг которой измеряется угол. Центр обычно обозначается точкой O.
2. Выберите начальную точку дуги (A) и конечную точку дуги (B), которые находятся на окружности.
3. Проведите прямую линию от центра окружности (O) до начальной точки дуги (A). Эта линия называется радиусом окружности.
4. Измерьте угол между радиусом окружности и сегментом, соединяющим центр окружности (O) с конечной точкой дуги (B).
5. Запишите измеренный угол, используя приставку «arc». Например, если измеренный угол равен 60 градусов, то он будет обозначаться как «60°» или «arc60°».

Использование приставки «arc» помогает ясно обозначить, что угол измеряется в контексте дуги и связан с окружностью. Это особенно полезно при работе с геометрическими задачами, связанными с окружностями и углами.

Видео по теме:

Вопрос-ответ:

Что означает приставка «arc» в математике?

Приставка «arc» в математике означает функцию, обратную тригонометрической функции. Например, арксинус (arcsin) — это функция, которая находит угол, значение синуса которого равно заданному числу.

Какие примеры использования приставки «arc» в математике?

Некоторые примеры использования приставки «arc» в математике включают: арксинус (arcsin), арккосинус (arccos), арктангенс (arctan), арккотангенс (arccot), арксеканс (arcsec) и арккосеканс (arccsc).

Как вычислить значение арксинуса?

Для вычисления значения арксинуса можно использовать обратную функцию синуса, обозначаемую как arcsin или sin^-1. Например, если sin(x) = 0.5, то можно вычислить arcsin(0.5), чтобы найти значение угла x, равного примерно 30 градусам.

Какие ограничения есть у арксинуса и других арктригонометрических функций?

Ограничения арктригонометрических функций, включая арксинус, заключаются в их области определения. Например, арксинус имеет область определения от -1 до 1, поскольку синус может принимать значения только в этом диапазоне. Значения арктригонометрических функций обычно выражаются в радианах.

Есть ли какие-то особенности использования арксинуса и других арктригонометрических функций?

Да, есть несколько особенностей использования арктригонометрических функций. Например, результат арктригонометрической функции может быть выражен в нескольких значениях, поскольку они обратным образом зависят от тригонометрических функций, которые могут иметь несколько периодов. Также следует обратить внимание на возможные ограничения и области определения каждой арктригонометрической функции.

Арккосинус и арктангенс: примеры использования приставки arc

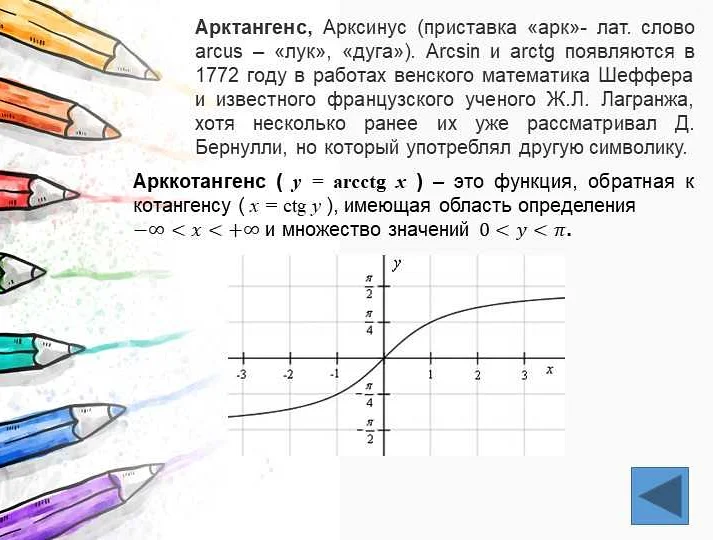
Арккосинус (arccos) — это обратная функция косинуса. Она определяет угол, значение косинуса которого равно заданному числу. Например, если известно, что косинус некоторого угла равен 0,5, то арккосинус этого числа будет равен 60° (или π/3 радиан).

Арктангенс (arctan) — это обратная функция тангенса. Она определяет угол, значение тангенса которого равно заданному числу. Например, если тангенс некоторого угла равен 1, то арктангенс этого числа будет равен 45° (или π/4 радиан).

Таблица ниже приводит несколько примеров использования приставки «arc» в контексте арккосинуса и арктангенса:

ФункцияАргументЗначение

arccos	0.5	60° (π/3 радиан)
arctan	1	45° (π/4 радиан)
arccos	-0.8	143.13° (2.498 радиана)
arctan	-1.5	-56.31° (-0.982 радиана)

Это лишь небольшая выборка примеров использования арккосинуса и арктангенса с приставкой «arc». Однако они демонстрируют основную идею этих функций и их практическое применение в решении задач из различных областей математики и физики.

Связь приставки arc с градусами и радианами

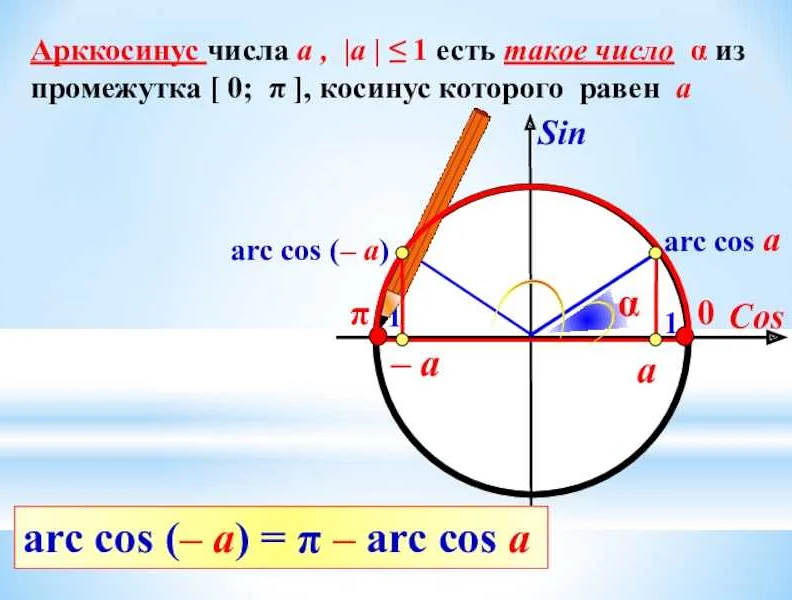
В математике приставка «arc» используется для обозначения функций, которые связаны с градусами и радианами. Эти функции позволяют вычислять углы и длины дуг на окружности.

Когда приставка «arc» используется перед тригонометрической функцией, например «arcsin» или «arccos», она указывает на обратную функцию. Например, «arcsin» вычисляет угол, значение синуса которого равно заданному числу. Аналогично, «arccos» вычисляет угол, значение косинуса которого равно заданному числу. В обоих случаях результатом будет угол в радианах.

Когда приставка «arc» используется перед функцией длины дуги, например «arclength», она указывает на функцию, которая вычисляет длину дуги на окружности. Длина дуги измеряется в радианах и зависит от радиуса окружности и величины угла.

Например, если у нас есть окружность радиусом 2π и мы хотим узнать длину дуги, соответствующей углу в 60 градусов, мы можем использовать функцию «arclength». Результатом будет значение, равное длине дуги в радианах, который можно преобразовать в другие единицы измерения, такие как метры или сантиметры.