Что такое сегмент в математике

Сегмент в математике — это часть прямой, ограниченная двумя точками. Он представляет собой участок прямой и может быть выражен в виде отрезка или полуотрезка. В статье рассмотрены основные свойства сегментов и их применение в различных задачах математики.

Сегмент — одно из базовых понятий геометрии, используемое для описания отрезка прямой. Он представляет собой часть прямой, ограниченную двумя точками, называемыми концами сегмента. Сегмент обозначается двумя точками, поставленными над линией, которую он ограничивает.

Сегмент обладает рядом свойств, которые важны при его изучении. Прежде всего, длина сегмента — это расстояние между его концами. Она может быть измерена с помощью специального инструмента, такого как линейка или масштабная лента. Кроме того, сегмент может быть удлинен или сокращен путем перемещения его концов.

Сегменты могут быть как прямыми, так и кривыми. В случае прямых сегментов, они могут быть горизонтальными, вертикальными или наклонными. Кривые сегменты, такие как дуги или окружности, также играют важную роль в геометрии и математике в целом.

Примеры использования сегментов в математике включают в себя построение графиков функций, измерение расстояний и моделирование физических объектов с помощью математических моделей.

В заключение, сегмент — это важное понятие в математике и геометрии, описывающее отрезок прямой, ограниченный двумя точками. Знание свойств и примеров использования сегментов помогает углубить понимание геометрии и применять ее в различных областях науки и техники.

Определение сегмента в математике

Сегмент можно представить с помощью символа «[]» или «()». Если у нас есть сегмент AB, то он записывается как [A, B] или (A, B). При этом точка A называется началом сегмента, а точка B — концом сегмента.

Сегмент может быть конечным или бесконечным. Конечный сегмент ограничен двумя точками и имеет фиксированную длину. Бесконечный сегмент не имеет конечных точек и простирается вдоль прямой в обе стороны.

В математике сегменты используются для измерения расстояний, построения графиков и решения различных задач.

Что такое сегмент?

Сегмент обозначается двумя точками, одной в начале и одной в конце, причем порядок точек важен для определения направления сегмента.

Сегмент имеет несколько ключевых свойств:

1. Длина сегмента — это расстояние между начальной точкой и конечной точкой сегмента. Она может быть вычислена с использованием формулы расстояния между двумя точками.
2. Сегмент перекрывается — это означает, что два сегмента имеют одну или несколько общих точек.
3. Расширение сегмента — это процесс увеличения длины сегмента путем добавления или удаления точек.

Примерами сегментов являются участки прямой между двумя городами, отрезки на оси координат, а также отрезки на графиках функций.

Из чего состоит сегмент?

Сегмент обладает следующими свойствами:

1. Начальная и конечная точки: Сегмент всегда имеет две точки — начальную и конечную. Они являются граничными точками сегмента и определяют его длину.

2. Длина: Длина сегмента равна расстоянию между его начальной и конечной точками. Она может быть измерена в единицах длины, таких как сантиметры, метры и т. д.

3. Внутренние точки: Внутренние точки сегмента находятся между его начальной и конечной точками. Они могут быть любыми точками на сегменте.

Сегмент может быть прямым, когда его начальная и конечная точки лежат на одной прямой, или наклонным, когда они лежат на разных прямых.

Примеры сегментов: AB, CD, EF и т. д.

Свойства сегментов

1. Сегмент имеет фиксированную длину.
2. Сегмент всегда прямой.
3. Сегмент может быть частью более длинной прямой.
4. Сегмент не имеет ни начала, ни конца.
5. Сегмент может быть частью фигуры, такой как треугольник, круг или многоугольник.
6. Сегмент может быть горизонтальным или вертикальным.

Эти свойства помогают определить и понять характеристики и связи сегментов в математике.

Свойство 1: Ограниченность

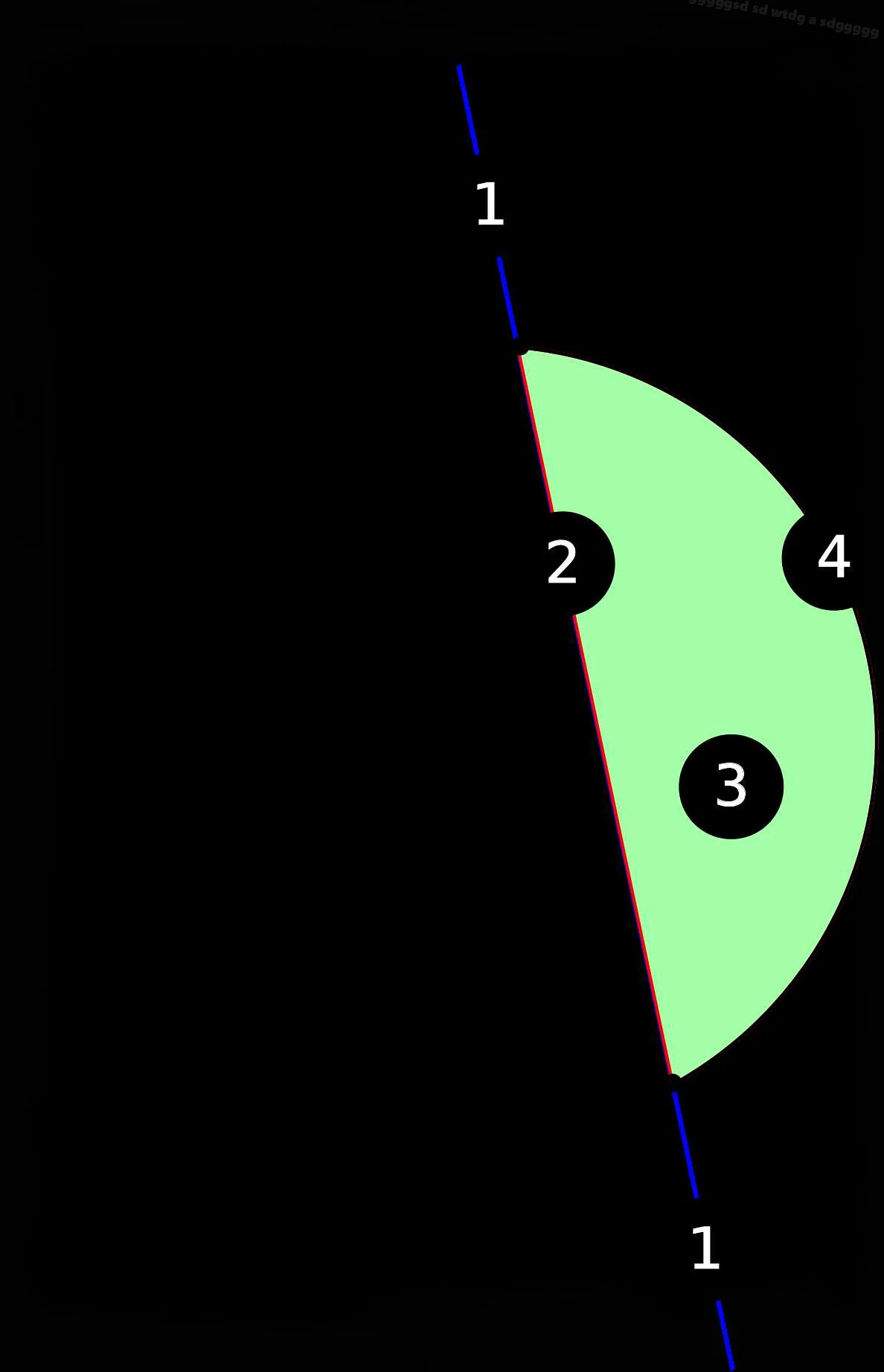
Ограниченность сегмента означает, что все точки этого сегмента находятся внутри границ этого участка, то есть лежат между начальной и конечной точками. Ни одна точка сегмента не может выходить за его границы.

В математике свойство ограниченности сегмента может быть выражено следующим образом:

• Для любой точки P на сегменте, координата которой лежит между координатами начальной и конечной точек сегмента, выполняется условие:
• xначальная ≤ xP ≤ xконечная

Примером сегмента с ограниченностью может служить отрезок прямой с начальной точкой (-3, 0) и конечной точкой (3, 0). Все точки этого отрезка находятся между этими двумя точками и не выходят за их границы.

Свойство 2: Принадлежность точек

Для определения принадлежности точки к сегменту необходимо проверить, лежит ли данная точка между начальной и конечной точками сегмента. Если точка находится на прямой, но вне сегмента, то она не принадлежит сегменту.

Принадлежность точек к сегменту можно выразить при помощи условий:

1. Внутри сегмента: Если точка лежит между начальной и конечной точками сегмента, то она принадлежит сегменту. Это можно записать как:

Точка А принадлежит сегменту BC, если А находится между B и C на прямой.

2. Вне сегмента: Если точка не лежит между начальной и конечной точками сегмента, то она не принадлежит сегменту. Это можно записать как:

Точка А не принадлежит сегменту BC, если А находится вне отрезка BC на прямой.

Пример:

Рассмотрим отрезок AB на числовой прямой, где A=-2 и B=3. Точка C=0 находится между A и B, поэтому она принадлежит сегменту AB. Однако, точка D=5 находится вне отрезка AB, поэтому она не принадлежит сегменту.

Примеры сегментов

1. Отрезок AB: это сегмент, который соединяет две точки A и B на плоскости. Он имеет начальную точку A и конечную точку B.
2. Луч CD: это сегмент, который имеет начальную точку C и бесконечно продолжается в одном направлении. Он также проходит через точку D.
3. Отрезок EF: это сегмент, который имеет начальную точку E и конечную точку F. Он может быть горизонтальным, вертикальным или наклонным.
4. Луч GH: это сегмент, который имеет начальную точку G и бесконечно продолжается в одном направлении. Он также проходит через точку H. Луч GH может быть горизонтальным, вертикальным или наклонным.

Это лишь несколько примеров сегментов, которые могут встретиться в геометрии. Сегменты играют важную роль в изучении форм и размеров объектов на плоскости и в пространстве.

Пример 1: Отрезок

Свойства отрезка:

СвойствоОписание

Длина	Расстояние между точками A и B
Середина отрезка	Точка, которая делит отрезок пополам
Симметричная точка	Точка, отраженная относительно середины отрезка

Пример: Пусть отрезок AB имеет длину 5 единиц. Его середина будет точка C, отраженная относительно середины точка D.

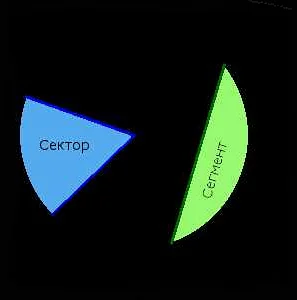
Пример 2: Часть окружности

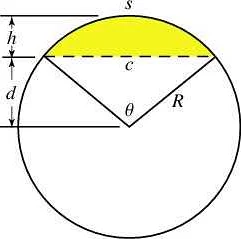
Рассмотрим окружность с центром в точке O и радиусом r. Отрежем от окружности часть, ограниченную двумя радиусами, образующими угол α (в радианах). Полученная фигура называется сектором окружности.

Сектор окружности имеет следующие свойства:

СвойствоФормула

Длина дуги	l = rα
Площадь сектора	S = (πr²α) / (2π) = (r²α) / 2

Например, если у нас есть окружность с радиусом 5 и сектор с углом в 45°, то:

Длина дуги: l = 5 * (45°) = 5 * (π/4) ≈ 5.5

Площадь сектора: S = (5² * (45°)) / 2 = 25 * (π/4) / 2 ≈ 19.63

Таким образом, сектор окружности является частью окружности, ограниченной двумя радиусами и имеющая свои уникальные свойства, такие как длина дуги и площадь.

Видео по теме:

Что такое сегмент в математике?

В математике сегмент — это часть прямой, ограниченная двумя точками. Сегмент обозначается двумя точками в скобках и над стрелкой, например, (A, B).

Как можно представить сегмент на координатной плоскости?

Сегмент на координатной плоскости можно представить в виде отрезка прямой, где его конечные точки имеют координаты (x1, y1) и (x2, y2). Таким образом, сегмент можно задать уравнением прямой, например, y = mx + b, где m и b — коэффициенты.

Какое отношение имеют сегмент и отрезок?

Сегмент и отрезок — это понятия, близкие по своему смыслу. Оба они представляют часть прямой, ограниченную двумя точками. Однако, отрезок — это конечная часть прямой, в то время как сегмент может быть как конечным, так и бесконечным.