Что означает слово вычислить в математике

Вычисление в математике подразумевает применение математических операций и алгоритмов для определения значения выражения или решения задачи. Узнайте, как работает процесс вычисления и какие методы используются в математике.

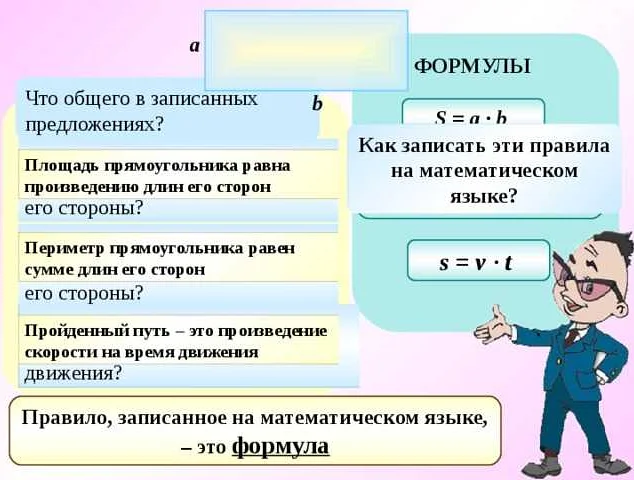
Вычислить – это процесс получения численного значения или результата математической операции. В математике слово «вычислить» используется для описания действия, которое позволяет получить точный ответ на поставленную задачу или выразить результат в виде числа или формулы.

Вычисления могут быть простыми или сложными, в зависимости от сложности задачи и используемых математических операций. Например, вычисление суммы двух чисел или нахождение площади прямоугольника являются простыми вычислениями, в то время как решение системы уравнений или вычисление интеграла – сложные вычисления, требующие более глубоких знаний и навыков.

Примеры вычислений в математике:

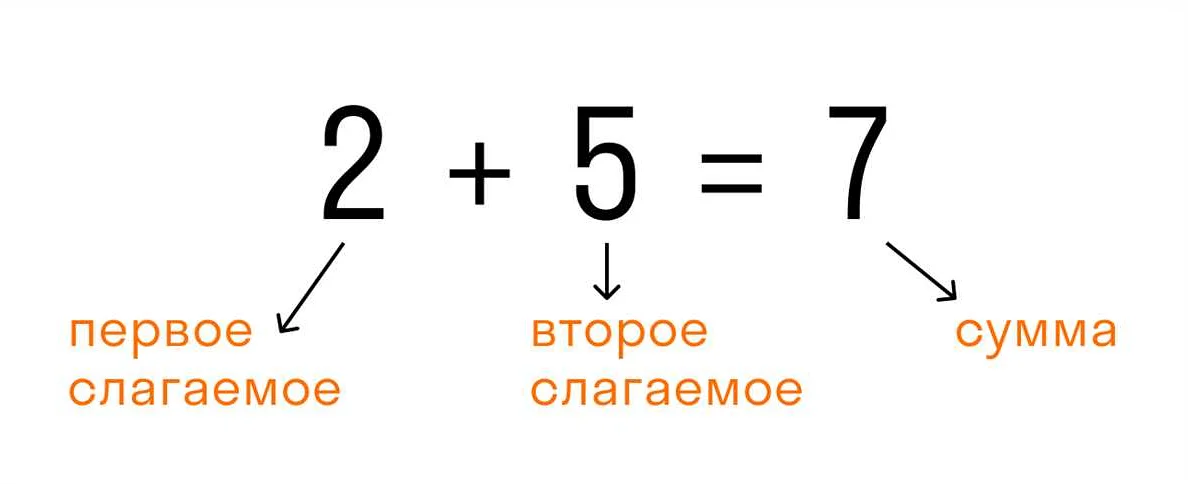
1. Вычисление суммы двух чисел:

Допустим, нам даны два числа: 5 и 7. Чтобы вычислить их сумму, мы просто складываем эти числа: 5 + 7 = 12. Таким образом, результатом вычисления будет число 12.

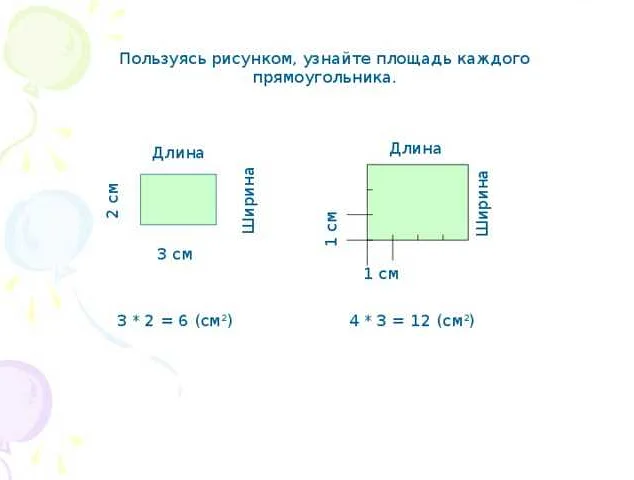
2. Вычисление площади прямоугольника:

Площадь прямоугольника можно вычислить, зная его длину и ширину. Например, если длина прямоугольника равна 5 единицам, а ширина – 3 единицам, то площадь будет равна произведению этих двух значений: 5 * 3 = 15. Таким образом, площадь прямоугольника составляет 15 единиц квадратных.

Таким образом, вычисление является неотъемлемой частью математики и позволяет нам получать точные численные значения или результаты различных математических операций. Оно используется для решения множества задач и задачей студента является правильное применение вычислительных методов для получения правильных результатов.

Определение понятия «вычислить» в математике

В математике, понятие «вычислить» относится к процессу получения численного значения или результата математического выражения или задачи. Вычисление может включать в себя выполнение арифметических операций, использование математических формул или алгоритмов для получения конечного ответа.

Вычисление может быть простым, например, при сложении двух чисел или умножении матриц, или сложным, включая более сложные операции, такие как интегрирование или решение дифференциальных уравнений.

Одним из важных аспектов вычислений в математике является точность результата. В зависимости от используемых методов и алгоритмов, можно достичь различной степени точности при вычислении. Точность может быть критической в некоторых областях математики, таких как численное моделирование или вычислительная физика.

В математике, вычисление является неотъемлемой частью решения задач и исследования математических моделей. Оно позволяет получить конкретные численные значения, которые могут быть использованы для анализа и понимания математических концепций и явлений.

Основные аспекты вычислений

В математике понятие «вычислить» означает выполнение определенных операций над числами или символами с целью получения результата. Основные аспекты вычислений включают в себя:

1. Арифметические операции: сложение, вычитание, умножение и деление. Вычисление происходит путем применения указанных операций к числам или символам.

Например, для вычисления выражения «2 + 3», необходимо сложить числа 2 и 3, что даст результат 5.

2. Алгебраические операции: раскрытие скобок, сокращение подобных членов, упрощение выражений. Вычисление выражений с помощью алгебраических операций позволяет упростить их и получить более компактную и понятную форму.

Например, для вычисления выражения «(2 + 3) * 4» необходимо сначала выполнить операцию в скобках, получив выражение «5 * 4», а затем умножить числа 5 и 4, получив результат 20.

3. Логические операции: конъюнкция, дизъюнкция, отрицание и импликация. Вычисление логических выражений позволяет определить истинность или ложность высказывания.

Например, для вычисления выражения «A и B», необходимо определить значения переменных A и B, а затем применить логическую операцию «и» к этим значениям. Если обе переменные равны истине, результат будет истиной, в противном случае — ложью.

4. Итерационные и рекурсивные процессы: циклы, рекурсивные функции. Вычисление включает в себя повторение операций или вызов функций для достижения желаемого результата.

Например, для вычисления факториала числа 5 можно использовать рекурсивную функцию, которая будет вызывать себя с уменьшенным аргументом до достижения базового случая.

Основные аспекты вычислений в математике позволяют получать точные и надежные результаты при решении различных задач. Понимание этих аспектов позволяет развивать логическое мышление и навыки работы с числами и выражениями.

Что означает «вычислить» в контексте математических задач

Вычислить в контексте математических задач означает выполнить последовательность операций или использовать алгоритм для получения численного результата.

В математике «вычислить» может относиться к различным операциям, таким как сложение, вычитание, умножение и деление. Например, если заданы два числа, то «вычислить их сумму» означает выполнить операцию сложения и получить численный результат.

Кроме того, «вычислить» может относиться к более сложным операциям, таким как вычисление корней, интегралов или производных. Например, «вычислить корень квадратный из числа» означает найти число, которое возводя в квадрат, даст заданное число.

В контексте математических задач, слово «вычислить» обычно подразумевает выполнение точных и строго определенных операций с числами или символами, с использованием правил и алгоритмов математики.

Вычисления и их роль в решении математических проблем

Вычисления играют важную роль в математике, позволяя нам решать различные математические проблемы. Они представляют собой процесс нахождения численных значений или результатов математических операций.

Вычисления могут быть простыми или сложными, в зависимости от того, какие операции выполняются и какие данные используются. Простые вычисления могут включать сложение, вычитание, умножение и деление чисел, а также применение базовых математических функций, таких как синус, косинус и тангенс.

Сложные вычисления могут включать использование сложных математических методов и алгоритмов для решения более сложных проблем. Например, вычисление интегралов, решение дифференциальных уравнений и поиск корней уравнений.

Вычисления также часто используются в прикладных науках, инженерии и технологиях для моделирования и симуляции различных процессов и явлений. Они позволяют нам предсказывать результаты и анализировать данные, что в свою очередь помогает нам принимать обоснованные решения и делать выводы.

В целом, вычисления являются важным инструментом в математике и науке. Они позволяют нам исследовать и понимать мир вокруг нас, а также решать различные проблемы и задачи, которые нам встречаются.

Примеры вычислений в математике

Пример 1: Вычисление площади прямоугольника.

Для вычисления площади прямоугольника необходимо умножить длину одной стороны на длину другой стороны. Например, если длина прямоугольника равна 4 см, а ширина равна 6 см, то площадь можно вычислить по формуле: Площадь = Длина x Ширина = 4 см x 6 см = 24 см².

Пример 2: Вычисление процента.

Для вычисления процента необходимо умножить число на процент и разделить на 100. Например, если нужно вычислить 20% от числа 50, то можно использовать формулу: 50 x 20 / 100 = 10.

Пример 3: Вычисление среднего значения.

Для вычисления среднего значения необходимо сложить все числа и разделить на их количество. Например, для чисел 5, 10, 15 и 20 среднее значение можно вычислить следующим образом: (5 + 10 + 15 + 20) / 4 = 12.5.

Это лишь несколько примеров вычислений, которые встречаются в математике. Они помогают получить точные результаты и применяются в различных областях, начиная от физики и химии, и заканчивая экономикой и финансами.

Как использовать вычисления для решения сложных задач

Одним из примеров использования вычислений является решение уравнений и систем уравнений. Путем применения математических операций, таких как сложение, вычитание, умножение и деление, мы можем найти значения переменных, удовлетворяющие условиям уравнений.

Вычисления также могут быть полезны для решения задач геометрии. Например, для нахождения площади треугольника или окружности, мы можем использовать соответствующие формулы и подставить значения известных параметров для получения точного результата.

Кроме того, вычисления могут быть применены для моделирования и анализа различных систем. Например, в физике мы можем использовать вычисления для определения движения тела или прогнозирования результатов эксперимента.

ПримерОписание

Решение квадратного уравнения	Методом вычислений можно найти значения x, удовлетворяющие уравнению ax^2 + bx + c = 0
Вычисление площади круга	Путем применения формулы S = πr^2, можно найти площадь круга с радиусом r
Моделирование движения тела	С помощью вычислений можно предсказать путь, скорость и ускорение тела, исходя из известных параметров

Таким образом, вычисления играют важную роль в решении сложных задач и помогают нам получать точные результаты в математике и других науках.

Различные методы вычислений в математике

Математика, как наука, предлагает различные методы вычислений, которые позволяют решать математические задачи и находить значения различных величин. Вот несколько из них:

Арифметические операции: это основные математические операции, такие как сложение, вычитание, умножение и деление. Они используются для выполнения простых вычислений и нахождения значений чисел и алгебраических выражений.

Алгебраические методы: в алгебре существуют различные методы вычислений, которые позволяют решать уравнения, системы уравнений, находить корни многочленов и т.д. Они основаны на алгоритмах и правилах преобразования алгебраических выражений.

Геометрические методы: в геометрии используются различные методы вычислений для нахождения площадей, объемов, углов и других характеристик фигур. Они основаны на геометрических формулах и свойствах фигур.

Математический анализ: это раздел математики, который занимается изучением пределов, производных, интегралов и других математических объектов, связанных с изменением и непрерывностью функций. В математическом анализе используются различные методы вычислений, такие как методы дифференцирования и интегрирования.

Вероятностные методы: в теории вероятностей и математической статистике используются различные методы вычислений, которые позволяют решать вероятностные задачи, определять вероятности событий, находить средние значения и дисперсии случайных величин и т.д.

Это только некоторые из методов вычислений, которые используются в математике. Каждый из них имеет свои особенности и применение в различных областях математики.

Важность точности при вычислениях

При вычислениях в математике, особенно при работе с большими числами или сложными формулами, даже небольшая ошибка в расчетах может привести к существенным искажениям результатов. Поэтому важно учитывать и контролировать точность вычислений.

Одним из ключевых методов обеспечения точности является выбор подходящей системы счисления. Например, при работе с числами с плавающей точкой, использование двоичной системы счисления может быть предпочтительным, чтобы избежать ошибок округления.

Дополнительно, при вычислениях с большим количеством операций, особенно если они повторяются множество раз, важно контролировать ошибки округления и накопление погрешностей. Для этого применяются различные методы, такие как использование точных арифметических операций, контроль и округление значений при необходимости.

Кроме того, важно учитывать точность входных данных и ошибки измерений при проведении математических расчетов. Несколько неточных или неточно измеренных величин могут значительно повлиять на результаты вычислений и привести к неточным выводам.

Пример 1:Пример 2:

При вычислении значения функции с использованием аппроксимации, небольшая погрешность может привести к существенным отклонениям от истинного значения функции.

При решении системы уравнений с большим числом неизвестных, даже малые погрешности в коэффициентах могут привести к существенным изменениям в результатах.

Таким образом, точность вычислений является важным аспектом в математике и требует особого внимания при решении задач. Только с помощью точных и надежных вычислений можно получить достоверные результаты и сделать правильные выводы.

Практическое применение вычислений в реальной жизни

В финансах вычисления помогают нам рассчитывать проценты, доходность инвестиций, а также прогнозировать финансовые показатели. Например, с помощью математических вычислений можно определить, какую сумму нужно вложить в банк, чтобы получить определенную выплату по процентам через определенное время.

Вычисления также используются в налоговой сфере. С помощью математических формул можно рассчитать сумму налога, амортизацию и другие финансовые показатели, которые необходимы для составления налоговой отчетности.

В других областях жизни, таких как инженерия, архитектура и наука, вычисления также играют важную роль. Они помогают в решении сложных технических задач, расчете конструкций и предсказании результатов экспериментов.

Вычисления также используются в медицине для анализа медицинских данных, расчета доз лекарств и прогнозирования результатов лечения.

Таким образом, вычисления имеют практическое применение во многих сферах жизни, помогая нам принимать обоснованные решения и предсказывать результаты различных процессов.

Вопрос-ответ:

Что означает слово «вычислить» в математике?

В математике слово «вычислить» означает получить численное значение выражения, решить задачу или определить значение переменной.

Как можно вычислить значение математического выражения?

Для вычисления значения математического выражения необходимо выполнить последовательность арифметических операций, указанных в выражении, и заменить переменные на их значения.

Какие примеры можно привести для понимания понятия «вычислить» в математике?

Примеры вычисления в математике могут включать расчеты площади фигуры, нахождение корней квадратного уравнения, вычисление значения функции в заданной точке и др.

Какими методами можно вычислить сложное математическое выражение?

Для вычисления сложного математического выражения можно использовать методы алгебры, геометрии, арифметики, численных методов или компьютерные программы.

Можно ли вычислить значение выражения с неизвестными переменными?

Да, можно. Если в выражении есть неизвестные переменные, то для их вычисления необходимо знать их значения или использовать уравнения, связывающие переменные, чтобы найти их значения.

Что означает слово «вычислить» в математике?

В математике, вычислить означает найти точное значение числа или функции с использованием определенных алгоритмов и формул. Это процесс, в результате которого мы получаем конкретный результат с заданной точностью.

Видео по теме: