Что обозначает в квадрате в математике

В математике выражение в квадрате обозначает, что число или выражение нужно возвести в квадрат. Это означает, что число нужно умножить на себя. Узнайте, как это работает и как применяется в различных математических задачах.

В математике символ в квадрате, выражаемый в виде верхнего индекса 2, имеет особое значение и является часто используемым обозначением для различных математических операций. Когда число или переменная ставятся в квадрат, это означает, что они умножаются на себя. Например, число 3 в квадрате обозначается как 3² и равно 3 * 3 = 9.

Операция возведения в квадрат имеет широкий спектр применений в различных областях математики, физики и инженерии. В алгебре и арифметике возведение числа в квадрат позволяет нам найти площадь квадрата с данной стороной или решить уравнения, связанные с квадратными корнями. В геометрии операция возведения в квадрат используется для нахождения площади прямоугольника или пространственной фигуры.

Возведение в квадрат также встречается в теории вероятности, статистике и исследовании данных. В этих областях квадрат числа используется для измерения разброса значений, определения распределения вероятностей и анализа вариативности.

Операция возведения в квадрат может быть использована и с переменными. Например, переменная x в квадрате, обозначаемая как x², равняется произведению x на саму себя. Это позволяет нам решать квадратные уравнения и проводить анализ функций в алгебре и математическом анализе.

В заключение, символ в квадрате в математике является мощным инструментом, который позволяет нам выполнять различные расчеты и обнаруживать закономерности в числах и переменных. Понимание этой операции важно для освоения различных областей математики и ее практического применения в решении задач и проблем, как в научных исследованиях, так и в повседневной жизни.

Значение в квадрате в математике

В математике выражение в квадрате означает, что значение этого выражения нужно возвести в квадрат. Выражение в квадрате обозначается символом «^2». Например, если дано число «а», его значение в квадрате будет обозначаться как «а^2».

Возвести число в квадрат означает умножить это число на само себя. То есть, если «а» — это число, то «а^2» равняется «а» умножить на «а». Например, если «а» равно 2, то «а^2» будет равно 4 (2*2 = 4).

Таким образом, значение в квадрате часто используется для определения площади квадрата или для решения различных математических задач. Например, если известна сторона квадрата, то его площадь можно найти, возвести эту сторону в квадрат.

Значение в квадрате также имеет свои свойства. Например, можно проводить операции с выражениями в квадрате, такие как сложение, вычитание, умножение и деление. Но для этого выражения должны иметь одинаковые основания. Например, «а^2 + b^2» можно сложить, но «а^2 + b» нельзя.

ВыражениеРезультат

2^2	4
(-3)^2	9
(x+1)^2	x^2 + 2x + 1

Таким образом, значение в квадрате в математике используется для возвышения числа в квадрат и определения площади квадрата. Оно также имеет свои свойства, которые позволяют проводить операции с выражениями в квадрате.

Подробное объяснение понятия «в квадрате»

В математике, выражение «в квадрате» относится к операции возведения числа во вторую степень. Когда число возводится в квадрат, его умножают на само себя.

Формально, выражение «в квадрате» записывается с помощью символа «^2» после числа. Например, 3^2 означает, что число 3 возводится во вторую степень.

Результатом возведения числа в квадрат является число, которое получается путем умножения этого числа на само себя. Например, 3^2 = 3 * 3 = 9. Таким образом, число 9 является результатом возведения числа 3 в квадрат.

Операция возведения в квадрат имеет ряд полезных свойств. Она позволяет нам вычислять площадь квадрата с известной стороной или находить квадратный корень из числа. Например, если площадь квадрата равна 16 квадратных единиц, то его сторона будет равна 4 (так как 4^2 = 16).

Также, операция возведения в квадрат может быть использована для обратной операции — извлечения квадратного корня. Если известно число, возведенное в квадрат, то можно найти его квадратный корень. Например, если число 25 является результатом возведения числа в квадрат (25 = 5^2), то его квадратный корень равен 5.

В квадрате — это одно из основных понятий в математике, которое широко используется в различных областях, включая геометрию, физику и алгебру.

Использование в квадрате в математических выражениях

В математике символ в квадрате (^2) используется для обозначения возведения числа в квадрат. Когда число стоит перед знаком в квадрате, оно умножается само на себя.

Например, число 5 в квадрате записывается как 5^2 и означает 5 * 5 = 25. Таким образом, число 5, возведенное в квадрат, равно 25.

Знак в квадрате также может использоваться для обозначения площади квадрата. Если сторона квадрата равна a, то его площадь можно выразить как a^2.

Кроме того, в квадрате могут быть выражены и другие математические объекты, такие как переменные или функции. Например, (x + 2)^2 обозначает квадрат суммы переменной x и числа 2.

Использование символа в квадрате в математических выражениях позволяет удобно обозначать возведение в квадрат, а также выражать площадь и другие математические операции.

В чем разница между возведением в квадрат и извлечением квадратного корня

Возведение в квадрат числа означает умножение этого числа на само себя. Например, квадрат числа 4 равняется 16, так как 4 умноженное на 4 равно 16. Обозначается так: 42 = 16. Возведение в квадрат позволяет нам найти площадь квадрата со стороной, равной данному числу.

Примечание: в алгебре, возведение в квадрат может также применяться к выражениям, не только к числам. Например, (x + 2)2 означает умножение выражения (x + 2) на само себя.

Извлечение квадратного корня числа, наоборот, позволяет нам найти число, при возведении которого в квадрат получается исходное число. Например, квадратный корень из 16 равен 4, так как 4 умноженное на 4 равно 16. Обозначается так: √16 = 4.

Примечание: извлечение квадратного корня может быть применено только к неотрицательным числам, поскольку квадрат корня всегда положителен или ноль.

Таким образом, возведение в квадрат и извлечение квадратного корня являются взаимообратными операциями, которые позволяют нам установить связь между числами и их квадратами.

Примеры использования в квадрате в математике

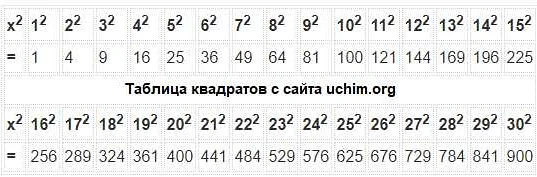
В математике символ в квадрате используется в различных контекстах. Вот несколько примеров его использования:

1. Возвести число в квадрат. Например, число 2 в квадрате обозначается как 22 и равно 4.
2. Вычисление площади квадрата. Площадь квадрата со стороной a обозначается как a2. Например, если сторона квадрата равна 5, то его площадь будет равна 52 = 25.
3. Вычисление суммы квадратов. Например, если у нас есть два числа a и b, то их сумма квадратов обозначается как a2 + b2. Например, если a = 3 и b = 4, то их сумма квадратов будет равна 32 + 42 = 9 + 16 = 25.
4. Вычисление квадратного корня. Обратная операция к возведению в квадрат — извлечение квадратного корня. Например, квадратный корень из числа 9 обозначается как √9 и равен 3.
5. Обозначение переменных. В алгебре символ в квадрате может использоваться для обозначения переменных. Например, x2 означает «x в квадрате», где x — переменная.

Это лишь некоторые примеры использования символа в квадрате в математике. Он широко используется в различных областях и имеет множество других интерпретаций и применений.

Свойства возведения числа в квадрат

Вот несколько свойств, которые связаны с возведением числа в квадрат:

1. Квадрат любого числа всегда положителен. Независимо от знака и значения числа, его квадрат всегда будет положительным числом.
2. Если число отрицательное, то его квадрат будет положительным числом. Например, (-2)² = 4.
3. Если число положительное, то его квадрат также будет положительным числом. Например, 3² = 9.
4. Квадрат суммы двух чисел равен сумме квадратов этих чисел, умноженной на 2, и их произведению. Например, (a + b)² = a² + 2ab + b².
5. Квадрат разности двух чисел равен разности квадратов этих чисел, умноженной на 2, и их произведению. Например, (a — b)² = a² — 2ab + b².

Эти свойства помогают в решении различных математических задач и упрощении выражений, содержащих квадраты чисел.

Возведение в квадрат как одна из математических операций

Для обозначения возведения в квадрат используется символ в виде числа, стоящего в верхнем индексе справа от числа. Например, 52 означает возведение числа 5 в квадрат, что равно 25.

Возведение в квадрат широко используется в различных областях математики и естественных науках. Например, оно применяется для решения квадратных уравнений, построения графиков параболы и анализа данных.

Кроме того, возведение в квадрат имеет ряд свойств, которые упрощают его использование. Например, квадрат суммы двух чисел равен сумме квадратов этих чисел, то есть (a + b)2 = a2 + 2ab + b2.

Таким образом, возведение в квадрат является важной математической операцией, которая позволяет получить квадрат числа и применяется в различных областях.

Вопрос-ответ:

Что означает в квадрате в математике?

В квадрате в математике означает, что число нужно умножить само на себя. Например, если у нас есть число 4 в квадрате, то это значит 4 * 4 = 16.

Какие еще способы обозначить в квадрате в математике?

В квадрате в математике можно обозначить также с помощью символа «^2». Например, число 5 в квадрате можно записать как 5^2.

Можно ли возвести в квадрат отрицательное число?

Да, можно возвести в квадрат и отрицательное число. Например, (-3)^2 = 9. В результате получится положительное число.

Какая разница между возвести в квадрат и вычислить квадратный корень?

Возвести число в квадрат означает умножить число само на себя. А вычислить квадратный корень означает найти число, которое при возведении в квадрат даст исходное число.

Какие другие операции можно выполнять с числами в квадрате?

С числами в квадрате можно выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление. Например, (2^2) + (3^2) = 4 + 9 = 13.

Зачем используется символ в квадрате в математике?

Символ в квадрате в математике используется для обозначения возведения числа в квадрат. Если число a возводится в квадрат, то это обозначается как a². То есть, a² означает a * a. Это позволяет удобно записывать и работать с такими операциями, особенно при работе с большими числами.

Каково значение числа в квадрате?

Значение числа в квадрате равно произведению этого числа на само себя. Например, 4 в квадрате (4²) равно 4 * 4 = 16. Таким образом, возведение числа в квадрат позволяет получить квадрат этого числа.

Практическое применение возведения в квадрат

1. Геометрия: Площадь квадрата. Если известна длина стороны квадрата, можно найти его площадь, возводя эту длину в квадрат.
2. Физика: Кинетическая энергия. Кинетическая энергия тела в движении пропорциональна квадрату его скорости.
3. Статистика: Дисперсия. Дисперсия используется для измерения разброса значений в выборке. Она вычисляется путем нахождения среднего квадратичного отклонения от среднего значения.
4. Инженерия: Электрическая мощность. Возведение напряжения в квадрат дает нам мощность в электрической цепи.
5. Финансы: Расчет процентов. При расчете сложных процентов, мы возводим (1 + процентная ставка) в квадрат для получения значения через несколько периодов.

Возведение в квадрат является одной из основных операций в математике и широко используется в различных областях науки и практической деятельности.

Видео по теме: