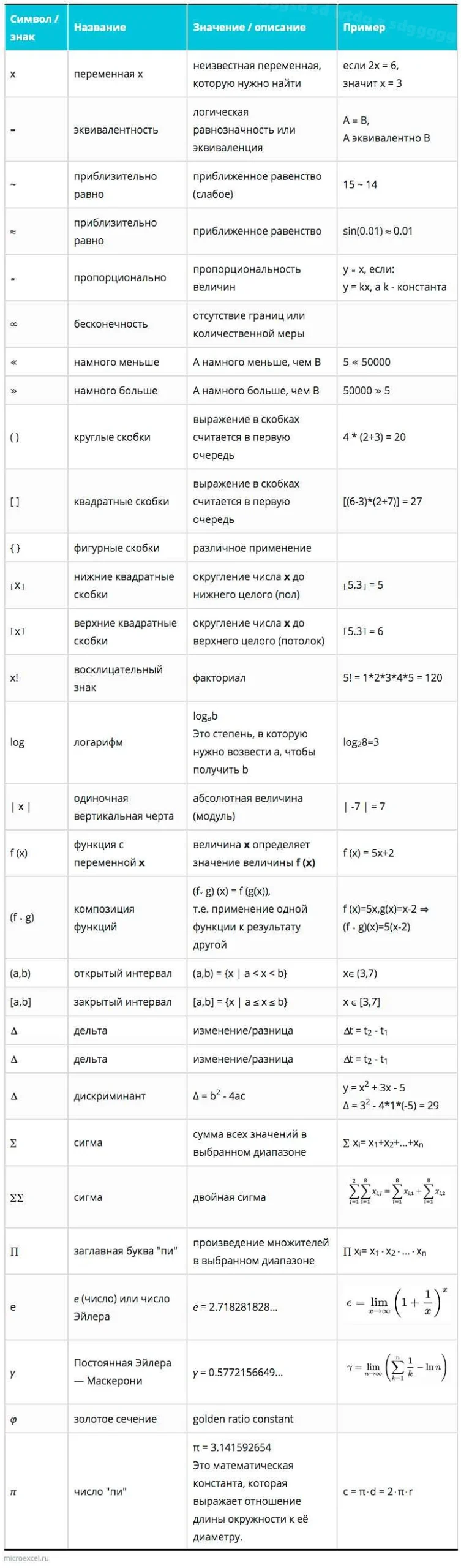
Что это за символ в математике

Символ в математике – это графическое обозначение, которое используется для представления определенных математических понятий или операций. В этой статье мы рассмотрим различные символы, их значения и применение в математике.

Математика — это наука, которая использует различные символы и обозначения для представления и обработки числовых и логических отношений. Одним из самых распространенных символов в математике является символ, который обозначает равенство — «=».

Символ «=» используется для обозначения равенства двух математических выражений. Он говорит о том, что значения двух выражений справа и слева от символа равны друг другу. Например, выражение «2 + 3 = 5» говорит о том, что сумма чисел 2 и 3 равна 5.

Символ «=» также используется для решения уравнений. Уравнение — это математическое выражение, содержащее символ «=», которое указывает на равенство двух выражений. Чтобы решить уравнение, нужно найти такое значение переменной, при котором оно будет выполняться. Например, уравнение «3x + 2 = 8» говорит о том, что выражение «3x + 2» равно 8. Решением этого уравнения будет значение переменной x, которое удовлетворяет равенству.

Пример: 3x + 2 = 8

Решение: x = 2

Символ «=» имеет большое значение в математике и используется в различных областях, включая алгебру, геометрию, анализ, статистику и др. Понимание и умение правильно использовать этот символ позволяет ученым и студентам работать с математическими выражениями, решать уравнения и проводить различные расчеты.

Что означает символ в математике: объяснение и примеры использования

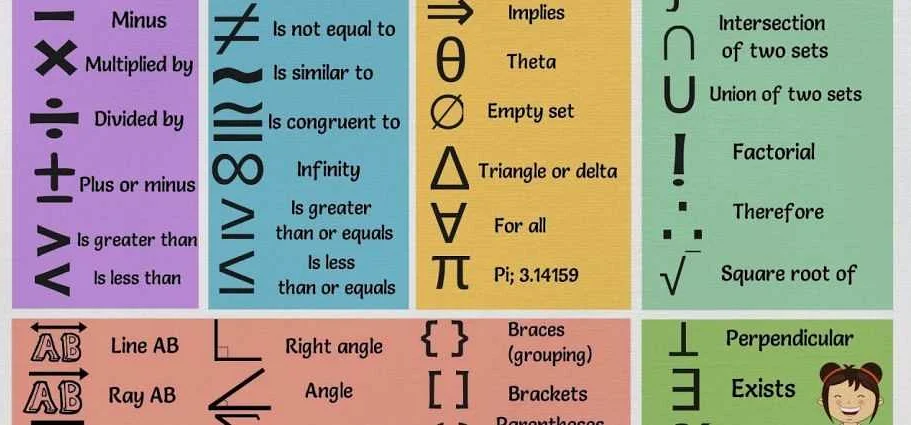
В математике символы используются для обозначения различных операций, свойств и объектов. Они помогают упростить запись и обмен информацией. В этом разделе мы рассмотрим некоторые из наиболее распространенных символов и их значения.

1. Символ «+»

Символ «+»используется для обозначения сложения. Например, выражение 2 + 3 означает, что нужно сложить числа 2 и 3, что даст результат 5.

2. Символ «-«

Символ «-» используется для обозначения вычитания. Например, выражение 5 — 3 означает, что нужно вычесть число 3 из числа 5, что даст результат 2.

3. Символ «×»

Символ «×» используется для обозначения умножения. Например, выражение 2 × 3 означает, что нужно умножить число 2 на число 3, что даст результат 6.

4. Символ «÷»

Символ «÷» используется для обозначения деления. Например, выражение 6 ÷ 2 означает, что нужно разделить число 6 на число 2, что даст результат 3.

5. Символ «=»

Символ «=» используется для обозначения равенства. Например, выражение 2 + 3 = 5 означает, что результат сложения чисел 2 и 3 равен числу 5.

6. Символ «≠»

Символ «≠» используется для обозначения неравенства. Например, выражение 2 + 3 ≠ 6 означает, что результат сложения чисел 2 и 3 не равен числу 6.

Это лишь некоторые из множества символов, используемых в математике. Знание и понимание этих символов помогает в анализе и решении математических задач.

Символы в математике: понятие и роль

Математика включает в себя огромное количество символов, которые используются для обозначения различных математических операций, объектов и свойств. Символы в математике играют важную роль, так как позволяют нам записывать и передавать математические идеи и концепции.

Символы в математике могут представлять собой буквы, цифры или специальные знаки. Они помогают сделать математические выражения более компактными и понятными. Кроме того, символы позволяют нам записывать уравнения, формулы и теоремы, которые являются основой различных областей математики.

Примерами символов в математике являются:

• Буквы латинского и греческого алфавитов, которые используются для обозначения переменных и констант. Например, x, y, a, b, α, β, γ.
• Знаки операций, такие как + (сложение), — (вычитание), * (умножение), / (деление).
• Символы отношений, такие как = (равенство), ≠ (неравенство), > (больше), < (меньше).
• Специальные символы, используемые в определенных областях математики, например, интеграл ∫, сумма ∑, бесконечность ∞.

Каждый символ в математике имеет свою собственную роль и значение. Они позволяют нам точно и компактно записывать и передавать математические идеи, что является основой для развития и применения математики в различных научных и инженерных областях.

Значение символов в математических выражениях

В математике символы играют важную роль в обозначении и описании различных математических операций и понятий. Знание значения этих символов позволяет понять смысл математических выражений и выполнять различные операции с числами и переменными.

Ниже приведены некоторые наиболее часто используемые символы в математических выражениях:

+ (плюс) — обозначает сложение двух чисел или выражений. Например, 2 + 3 = 5.

— (минус) — обозначает вычитание одного числа или выражения из другого. Например, 5 — 2 = 3.

* (умножение) — обозначает умножение двух чисел или выражений. Например, 2 * 3 = 6.

/ (деление) — обозначает деление одного числа или выражения на другое. Например, 6 / 2 = 3.

= (равенство) — обозначает, что два выражения равны между собой. Например, 2 + 3 = 5.

< (меньше) — обозначает, что одно число меньше другого. Например, 2 < 3.

> (больше) — обозначает, что одно число больше другого. Например, 3 > 2.

≤ (меньше или равно) — обозначает, что одно число меньше или равно другому. Например, 2 ≤ 3.

≥ (больше или равно) — обозначает, что одно число больше или равно другому. Например, 3 ≥ 2.

() (скобки) — используются для определения порядка выполнения операций в математическом выражении. Например, (2 + 3) * 4 = 20.

π (пи) — математическая константа, равная отношению длины окружности к ее диаметру. Пример использования: площадь круга равна π * r^2.

√ (корень) — обозначает извлечение квадратного корня из числа или выражения. Например, √25 = 5.

∑ (сумма) — обозначает суммирование ряда чисел. Например, ∑(1, 2, 3) = 6.

Это лишь некоторые примеры символов, используемых в математике. Знание значения этих символов позволяет лучше понимать математические выражения и решать различные задачи.

Арифметические символы: основные виды и их значения

В таблице ниже приведены основные арифметические символы и их значения:

СимволЗначение

+	Сложение
—	Вычитание
*	Умножение
/	Деление
^	Возведение в степень
√	Квадратный корень

Символ «+» используется для обозначения операции сложения. Например, выражение 2 + 3 означает, что нужно сложить числа 2 и 3.

Символ «-» используется для обозначения операции вычитания. Например, выражение 5 — 3 означает, что нужно вычесть число 3 из числа 5.

Символ «*» используется для обозначения операции умножения. Например, выражение 2 * 4 означает, что нужно умножить число 2 на число 4.

Символ «/» используется для обозначения операции деления. Например, выражение 10 / 2 означает, что нужно разделить число 10 на число 2.

Символ «^» используется для обозначения операции возведения в степень. Например, выражение 2^3 означает, что нужно возвести число 2 в степень 3.

Символ «√» используется для обозначения операции извлечения квадратного корня. Например, выражение √9 означает, что нужно найти квадратный корень числа 9.

Знание арифметических символов позволяет более точно и ясно записывать и решать математические задачи.

Символы в логических выражениях: обозначение и функции

В математике и логике существуют специальные символы, которые используются для обозначения логических выражений. Эти символы позволяют записать и выразить различные логические операции, такие как конъюнкция, дизъюнкция, отрицание и импликация.

Один из основных символов в логических выражениях — это символ «&», который обозначает логическую конъюнкцию. Он используется для объединения двух логических выражений таким образом, что истина будет только в том случае, если оба выражения истинны.

Другой важный символ — это символ «∨», который обозначает логическую дизъюнкцию. Он используется для объединения двух логических выражений таким образом, что истина будет в том случае, если хотя бы одно из выражений истинно.

Символ «¬» обозначает отрицание и используется для инверсии значения логического выражения. Если исходное выражение истинно, то после применения символа отрицания оно станет ложным, и наоборот.

Один из сложных символов — это символ «→», который обозначает импликацию. Он используется для выражения условия, при котором одно выражение следует из другого. Если условие истинно, то и выражение, следующее за символом, также будет истинным.

В логических выражениях можно комбинировать указанные символы, используя их для записи сложных логических выражений. Например, выражение «(A ∨ B) & (¬C → D)» использует символы дизъюнкции, конъюнкции, отрицания и импликации для выражения сложного условия.

Знание и понимание символов в логических выражениях позволяет более точно и компактно записывать и анализировать различные логические утверждения и рассуждения.

Символы в геометрии: их назначение и использование

СимволНазначениеПример использования

∠	Обозначает угол	∠ABC — угол, образованный линиями AB и BC
∡	Обозначает угол	∡XYZ — угол, образованный линиями XY и YZ
⊥	Обозначает перпендикулярность	AB ⊥ CD — отрезки AB и CD перпендикулярны друг другу
∥	Обозначает параллельность	AB ∥ CD — отрезки AB и CD параллельны друг другу
△	Обозначает треугольник	△ABC — треугольник, образованный точками A, B и C
◦	Обозначает окружность	◦O — окружность с центром в точке O

Это лишь некоторые из символов, используемых в геометрии. Они помогают наглядно представить информацию и сделать геометрические выкладки более понятными. Знание и понимание этих символов позволяет работать с геометрическими фигурами и решать задачи эффективно.

Символы в статистике и вероятности: примеры и интерпретация

Ниже приведены примеры некоторых основных символов, используемых в статистике и вероятности:

• μ (мю): символ обозначает математическое ожидание или среднее значение. Например, если X — случайная величина, то μX представляет собой среднее значение этой величины.
• σ (сигма): символ обозначает стандартное отклонение. Он показывает, насколько значения случайной величины отклоняются от ее среднего значения. Чем больше значение σ, тем больше разброс значений.
• Σ (сумма): символ обозначает сумму. Например, ΣXi обозначает сумму всех значений Xi.
• λ (лямбда): символ обозначает интенсивность или параметр распределения. Например, в экспоненциальном распределении λ обозначает среднее число событий, происходящих за единицу времени.
• p (пи): символ обозначает вероятность. Например, p(A) обозначает вероятность события A.
• α (альфа): символ обозначает уровень значимости или вероятность ошибки первого рода. Это вероятность отвергнуть верную нулевую гипотезу.
• β (бета): символ обозначает вероятность ошибки второго рода. Это вероятность принять неверную нулевую гипотезу.

Это только некоторые из символов, используемых в статистике и вероятности. Знание и понимание этих символов помогает упростить и систематизировать анализ случайных явлений и проведение статистических исследований.

Символы в алгебре: роль и способы применения

Символы играют важную роль в алгебре, предоставляя нам удобные обозначения для математических объектов и операций. Они позволяют нам записывать сложные выражения и уравнения компактно и ясно.

Одним из наиболее распространенных символов в алгебре является символ умножения «×». Он используется для обозначения операции умножения между числами, переменными или другими математическими объектами. Например, выражение «2 × 3» означает умножение числа 2 на число 3.

Еще одним важным символом в алгебре является символ равенства «=». Он используется для обозначения равенства между двумя выражениями или математическими объектами. Например, уравнение «x + 2 = 5» означает, что сумма переменной «x» и числа 2 равна числу 5.

Также в алгебре используются символы для обозначения различных операций, таких как сложение «+», вычитание «-«, деление «÷» и возведение в степень «^». Они позволяют нам записывать и решать различные математические задачи и уравнения.

Для более сложных выражений и уравнений алгебра также использует символы скобок «(«, «)» и фигурных скобок «{«, «}». Они позволяют нам группировать математические объекты и указывать порядок выполнения операций. Например, выражение «(2 + 3) × 4» означает, что сначала нужно выполнить сложение чисел 2 и 3, а затем умножить результат на число 4.

В таблице ниже приведены некоторые распространенные символы в алгебре и их значения:

СимволЗначение

+	Сложение
—	Вычитание
×	Умножение
÷	Деление
=	Равенство
^	Возведение в степень
( )	Скобки
{ }	Фигурные скобки

В заключение, символы в алгебре играют важную роль в обозначении и решении математических задач. Они позволяют нам записывать выражения и уравнения более компактно и ясно. Знание и умение использовать символы в алгебре является важной частью математического образования и позволяет более эффективно работать с математическими объектами и операциями.

Символы в теории чисел: объяснение и важность

В теории чисел символы играют важную роль и используются для обозначения различных математических объектов и свойств. Они позволяют удобно записывать и обозначать различные формулы, теоремы и определения.

Один из наиболее известных символов в теории чисел — это символ простого числа. Простые числа являются основными строительными блоками в теории чисел, и их свойства и взаимодействия изучаются с помощью символа простого числа. Этот символ обозначает, что число является простым и не имеет делителей, кроме 1 и самого себя.

Еще одним важным символом в теории чисел является символ делителя. Он используется для обозначения делителей числа. Например, если число А делится на число В без остатка, то записывается символ A | B. Этот символ позволяет удобно выражать свойства и отношения между числами.

Символы также используются для обозначения различных операций и функций в теории чисел. Например, символ суммы обозначается знаком «Сигма» и используется для записи суммы ряда чисел. Символы также могут обозначать различные функции, такие как функция Эйлера, функция Мебиуса и др.

Использование символов в теории чисел позволяет удобно записывать и передавать информацию о свойствах чисел и их взаимосвязях. Они упрощают математические выкладки и позволяют делать более точные и точные выводы. Поэтому понимание и использование символов в теории чисел является важным аспектом для всех, кто занимается изучением этой области математики.

Вопрос-ответ:

Зачем нужны символы в математике?

Символы в математике используются для обозначения различных математических операций, формул, выражений и концепций. Они помогают нам записывать и передавать математическую информацию более компактно и точно.

Что означает символ «+» в математике?

Символ «+» в математике обозначает операцию сложения. Например, если у нас есть числа 2 и 3, то «2 + 3» означает их сложение, и результатом будет число 5.

Какой символ используется для обозначения умножения в математике?

Символ «×» (знак умножения) используется для обозначения операции умножения в математике. Например, если у нас есть числа 4 и 5, то «4 × 5» означает их умножение, и результатом будет число 20.

Что означает символ «≠» в математике?

Символ «≠» (знак неравенства) используется для обозначения отрицания равенства в математике. Например, если у нас есть два числа, скажем, 2 и 3, то «2 ≠ 3» означает, что эти числа не равны друг другу. Этот символ часто используется в уравнениях и неравенствах.

Видео по теме: