Что обозначает математический знак

Математические знаки используются для обозначения различных операций и отношений в математике. В этой статье рассмотрим основные математические знаки и их значения, такие как сложение, вычитание, умножение, деление, равенство, неравенство и многое другое. Узнайте, как правильно использовать математические знаки и как они помогают в решении математических задач.

Математика — это наука, которая изучает числа, структуры и пространства, используя логические и абстрактные методы. Одним из ключевых элементов математики являются математические знаки, которые используются для обозначения различных операций и отношений между числами и объектами.

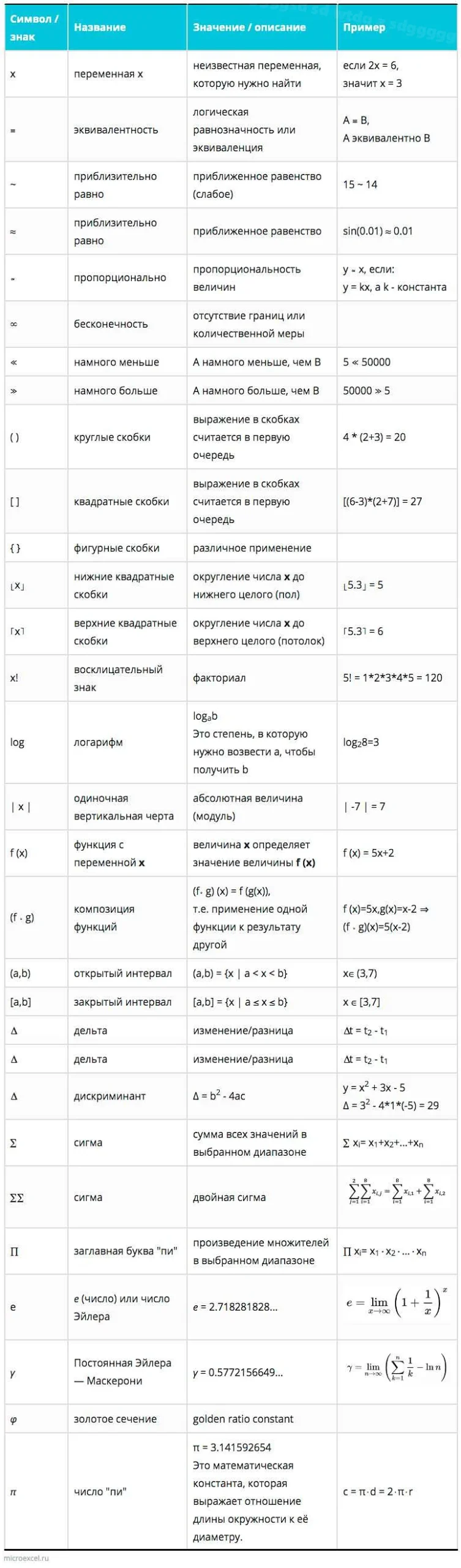
Одним из наиболее известных математических знаков является знак «плюс» (+), который обозначает сложение двух чисел. Например, 2 + 3 = 5. Знак «минус» (-) обозначает вычитание, например, 5 — 3 = 2.

Еще один важный математический знак — это знак «умножить» (×), который обозначает умножение двух чисел. Например, 2 × 3 = 6. Знак «делить» (÷) обозначает деление, например, 6 ÷ 2 = 3.

Математические знаки также используются для обозначения отношений между числами. Например, знак «больше» (>) используется для сравнения двух чисел, где 5 > 3. Знак «меньше» (

Еще один важный математический знак — это знак «равно» (=), который обозначает, что два выражения или числа равны друг другу. Например, 2 + 3 = 5.

Это лишь небольшая часть математических знаков, которые используются в математике. Они помогают нам проводить различные операции и сравнения чисел и объектов. Понимание этих знаков очень важно для успешного изучения математики и их применения в реальной жизни.

Значение математических знаков: основные понятия и примеры

1. Знак «+»: обозначает операцию сложения. Например, выражение «2 + 3» означает сложение чисел 2 и 3, результатом которого будет число 5.

2. Знак «-«: обозначает операцию вычитания. Например, выражение «5 — 2» означает вычитание числа 2 из числа 5, результатом которого будет число 3.

3. Знак «×» или «*»: обозначает операцию умножения. Например, выражение «4 × 3» означает умножение чисел 4 и 3, результатом которого будет число 12.

4. Знак «÷» или «/»: обозначает операцию деления. Например, выражение «10 ÷ 2» означает деление числа 10 на число 2, результатом которого будет число 5.

5. Знак «√»: обозначает операцию извлечения квадратного корня. Например, выражение «√9» означает извлечение квадратного корня из числа 9, результатом которого будет число 3.

6. Знак «=»: обозначает операцию сравнения. Например, выражение «2 + 3 = 5» означает, что результатом сложения чисел 2 и 3 является число 5.

7. Знаки «»: обозначают операцию сравнения «меньше» и «больше» соответственно. Например, выражение «5 > 3» означает, что число 5 больше числа 3.

8. Знаки «≤» и «≥»: обозначают операцию сравнения «меньше или равно» и «больше или равно» соответственно. Например, выражение «4 ≤ 4» означает, что число 4 меньше или равно числу 4.

9. Знаки «(«, «)» и «[]»: обозначают группировку выражений и порядок выполнения операций. Например, выражение «2 × (3 + 4)» означает, что сначала выполняется операция сложения, а затем умножения числа 2 на результат сложения чисел 3 и 4.

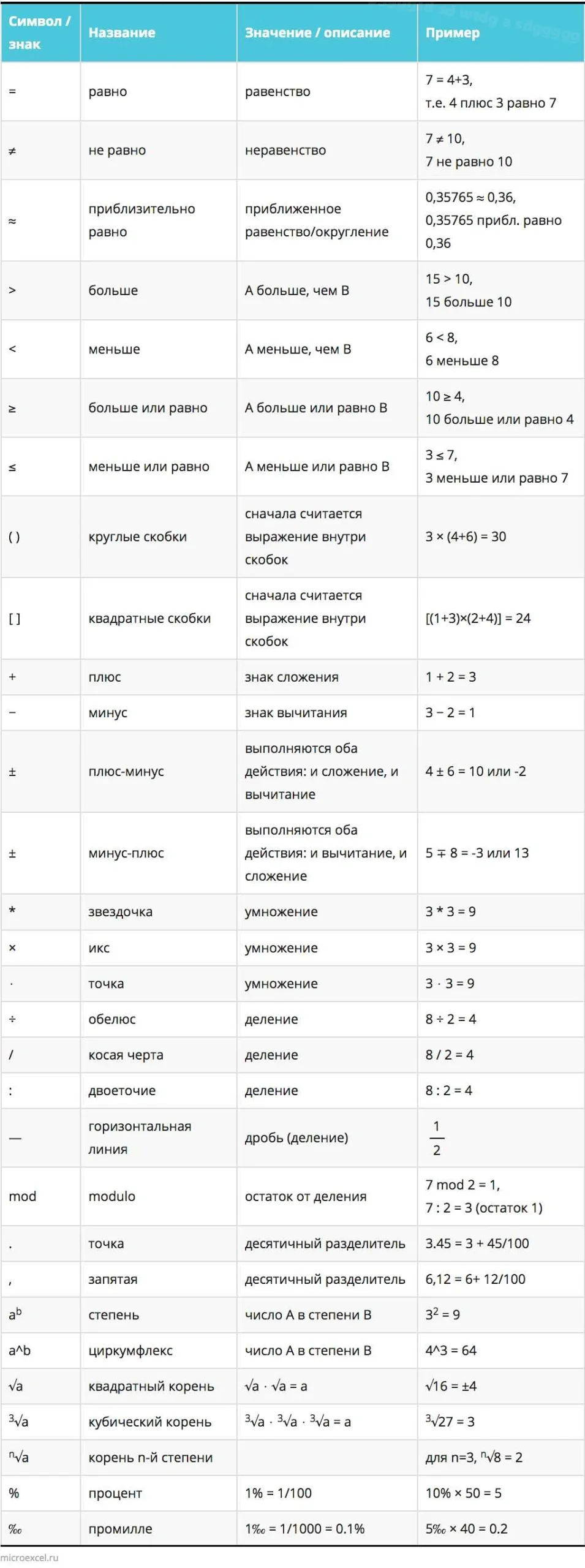
ЗнакЗначениеПример

+	Сложение	2 + 3 = 5
—	Вычитание	5 — 2 = 3
×	Умножение	4 × 3 = 12
÷	Деление	10 ÷ 2 = 5
√	Извлечение квадратного корня	√9 = 3
=	Сравнение	2 + 3 = 5
<	Меньше	5 < 3
>	Больше	5 > 3
≤	Меньше или равно	4 ≤ 4
≥	Больше или равно	4 ≥ 4

Таким образом, математические знаки позволяют нам оперировать числами и выражать различные математические операции и отношения. Они служат основой для построения математических выражений и формул, которые широко используются в науке, технике, экономике и других областях.

Плюс и минус в математике: основные операции

Знак «плюс» (+) обозначает сложение чисел. Например, если у нас есть числа 5 и 3, то их сумма будет равна 8:

• 5 + 3 = 8

Знак «минус» (-) обозначает вычитание чисел. Например, если у нас есть число 7 и мы вычитаем из него число 4, то получим результат 3:

• 7 — 4 = 3

Также знак «минус» может использоваться для обозначения отрицательных чисел. Например, если число -2, то его можно записать как -2.

При выполнении операций со знаками плюс и минус необходимо учитывать их приоритет. Умение правильно использовать эти знаки является важным навыком в математике.

Умножение и деление: обозначения и правила выполнения

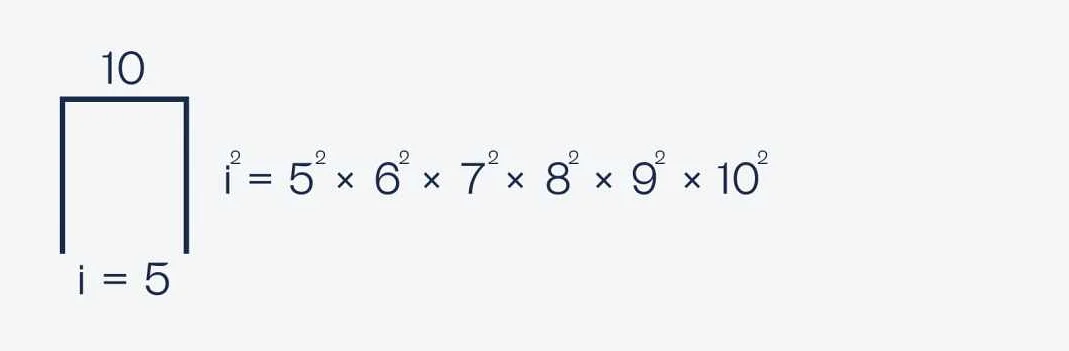
Знак умножения обозначается символом «×» или «*». Например, если нужно умножить число 2 на число 3, запись будет выглядеть следующим образом: 2 × 3 или 2 * 3. Правила выполнения умножения состоят в следующем:

1. Умножение числа на 0 всегда дает 0. Например, 5 × 0 = 0.
2. Умножение числа на 1 не изменяет его значение. Например, 5 × 1 = 5.
3. Коммутативность. Порядок перемножения чисел не влияет на результат. Например, 2 × 3 = 3 × 2.
4. Ассоциативность. Порядок выполнения умножения не влияет на результат. Например, (2 × 3) × 4 = 2 × (3 × 4).

Знак деления обозначается символом «÷» или «/». Например, если нужно разделить число 6 на число 2, запись будет выглядеть следующим образом: 6 ÷ 2 или 6 / 2. Правила выполнения деления:

1. Деление на 0 невозможно. Результат деления на 0 не определен.
2. Деление числа на 1 не изменяет его значение. Например, 6 ÷ 1 = 6.
3. Деление числа на само себя всегда равно 1. Например, 8 ÷ 8 = 1.
4. Коммутативность не выполняется. Порядок деления влияет на результат. Например, 4 ÷ 2 ≠ 2 ÷ 4.

Умножение и деление очень важны в математике и широко применяются в повседневной жизни. Они позволяют решать задачи, связанные с расчетами, соотношениями и пропорциями. Правильное применение обозначений и правил выполнения этих операций помогает получить точные и верные результаты.

Скобки и их значение в математике: порядок выполнения операций

Существуют два типа скобок: круглые скобки () и квадратные скобки []. Круглые скобки обычно используются для группировки выражений, а квадратные скобки могут использоваться для указания индекса или обозначения массива.

Порядок выполнения операций с использованием скобок следует следующим правилам:

1. Выполняются операции внутри скобок в первую очередь.
2. Далее выполняются операции с учетом приоритета операций (умножение, деление, сложение, вычитание).
3. Если в выражении присутствуют несколько пар скобок, сначала выполняются операции внутри самых внутренних скобок.

Например, в выражении (2 + 3) * 4 сначала выполняется операция внутри скобок (2 + 3), а затем результат умножается на 4. Результатом этого выражения будет 20.

Если нужно изменить порядок выполнения операций, можно использовать скобки. Например, в выражении 2 + 3 * 4 сначала будет выполнено умножение (3 * 4), а затем сложение с числом 2. Результатом этого выражения будет 14.

Таким образом, скобки играют важную роль в определении порядка выполнения операций в математике. Правильное использование скобок помогает получить точный и ожидаемый результат вычислений.

Знаки равенства и неравенства: сравнение и доказательства

В математике знаки равенства и неравенства играют важную роль при сравнении чисел и выражений. Знак равенства (=) используется для указания того, что два математических объекта или выражения имеют одинаковое значение. Например, 2 + 3 = 5 означает, что сумма чисел 2 и 3 равна 5.

Знак неравенства (<>) указывает на то, что два объекта или выражения имеют различные значения. Например, 4 + 2 <> 7 означает, что сумма чисел 4 и 2 не равна 7.

Часто в математике требуется сравнить значения различных выражений или чисел. Для этого используются следующие знаки неравенства:

• Больше (>). Знак больше указывает на то, что значение выражения слева от знака больше значения выражения справа. Например, 6 > 3 означает, что число 6 больше числа 3.
• Меньше ( Знак меньше указывает на то, что значение выражения слева от знака меньше значения выражения справа. Например, 2 < 5 означает, что число 2 меньше числа 5.
• Больше или равно (≥). Знак больше или равно означает, что значение выражения слева от знака больше или равно значению выражения справа. Например, 5 + 3 ≥ 7 означает, что сумма чисел 5 и 3 больше или равна 7.
• Меньше или равно (≤). Знак меньше или равно означает, что значение выражения слева от знака меньше или равно значению выражения справа. Например, 4 — 1 ≤ 3 означает, что разность чисел 4 и 1 меньше или равна 3.

Доказательства неравенств могут быть полезными при решении математических задач. Для доказательства неравенства часто используются алгебраические преобразования и свойства чисел. Например, чтобы доказать, что 2x + 3 > 7, можно вычесть 3 из обеих частей неравенства и получить 2x > 4. Затем, разделив обе части неравенства на 2, получаем x > 2, что является решением данного неравенства.

Проценты и десятичные дроби: расчеты и применение

Проценты обозначаются знаком «%». Они представляют собой долю от 100. Например, 25% означает 25 долей из 100. Проценты используются для выражения отношений, а также для обозначения изменений и роста.

Расчеты с процентами могут быть выполнены с использованием десятичных дробей. Десятичные дроби представляют числа, записанные с десятичной точкой. Например, число 0,5 представляет половину, а число 0,75 представляет 75 долей из 100.

Для перевода процентов в десятичные дроби, необходимо разделить значение процента на 100. Например, 50% можно перевести в десятичную дробь, разделив 50 на 100, что равно 0,5.

Для расчета значения процента от числа, необходимо умножить число на десятичную дробь, соответствующую проценту. Например, чтобы найти 20% от числа 100, нужно умножить 100 на 0,2, что равно 20.

Проценты и десятичные дроби широко применяются в финансовых расчетах, в торговле и в различных сферах бизнеса. Они позволяют нам сравнивать различные значения, определять изменения и рост, а также проводить простые и сложные математические операции.

Возведение в степень и извлечение корня: операции с показателями

В математике существуют операции, которые позволяют выполнять возведение в степень и извлечение корня числа. Эти операции основаны на использовании показателей, которые указывают, сколько раз нужно умножить число само на себя или сколько раз нужно извлечь корень из числа.

Возведение в степень обозначается с помощью символа «^» или «**». Например, 2^3 или 2**3 означает, что число 2 нужно умножить на себя три раза: 2 * 2 * 2 = 8. Показатель степени может быть как положительным, так и отрицательным. При положительном показателе число умножается на себя указанное количество раз, а при отрицательном показателе происходит деление числа на себя указанное количество раз. Например, 2^(-3) означает, что число 2 нужно разделить на себя три раза: 1 / (2 * 2 * 2) = 1/8.

Извлечение корня обозначается с помощью символа «√». Например, √9 означает, что нужно найти число, которое умноженное на себя даст 9. В данном случае это число 3, так как 3 * 3 = 9. Показатель корня указывает, какой корень нужно извлечь из числа. Например, √(8^2) означает, что нужно извлечь корень квадратный из числа 8^2, то есть из числа 64. Результатом будет число 8, так как 8 * 8 = 64.

Показатели могут быть рациональными числами, что позволяет выполнять операции с дробными степенями и корнями. Например, 4^(1/2) означает, что нужно извлечь корень квадратный из числа 4, что равно 2. А 27^(1/3) означает, что нужно извлечь корень кубический из числа 27, что равно 3.

Возведение в степень и извлечение корня являются важными математическими операциями, которые широко применяются не только в математике, но и в других науках и областях знания.

Знаки суммы и разности: вычисление сумм и разностей

Операция сложения может быть выполнена не только с двумя числами, но и с более чем двумя. Например, выражение 1 + 2 + 3 означает, что нужно сложить числа 1, 2 и 3, что даст в результате число 6.

Знак суммы также может использоваться для обозначения объединения множеств. Например, если A и B — два множества, то запись A + B означает объединение этих множеств.

Знак разности (-) используется для обозначения вычитания одного числа из другого. Например, выражение 5 — 3 означает, что нужно вычесть число 3 из числа 5, что даст в результате число 2.

Операция вычитания может быть выполнена не только с двумя числами, но и с более чем двумя. Например, выражение 10 — 2 — 3 означает, что нужно вычесть числа 2 и 3 из числа 10, что даст в результате число 5.

Знак разности также может использоваться для обозначения разности между элементами множеств. Например, если A и B — два множества, то запись A — B означает разность между этими множествами.

Использование знаков суммы и разности в математике позволяет проводить операции сложения и вычитания с числами и элементами множеств, что является одной из основных задач математического анализа и алгебры.

Вопрос-ответ:

Что означает знак «+» в математике?

Знак «+» в математике обозначает операцию сложения. Он используется для объединения двух или более чисел в одну сумму. Например, в выражении «2 + 3» знак «+» указывает на то, что нужно сложить числа 2 и 3, что дает результат 5. Знак «+» также может использоваться для указания положительного направления числовой оси.

Что означает знак «-» в математике?

Знак «-» в математике имеет несколько значений. Во-первых, он может обозначать операцию вычитания. Например, в выражении «5 — 3» знак «-» указывает на то, что нужно вычесть число 3 из числа 5, что дает результат 2. Во-вторых, знак «-» может использоваться для указания отрицательного направления числовой оси. Например, -3 означает число, которое находится на 3 единицы влево от нуля. Кроме того, знак «-» может использоваться для обозначения отрицательного числа.

Что означает знак «×» в математике?

Знак «×» в математике обозначает операцию умножения. Он используется для умножения двух или более чисел. Например, в выражении «2 × 3» знак «×» указывает на то, что нужно умножить числа 2 и 3, что дает результат 6.

Что означает знак «÷» в математике?

Знак «÷» в математике обозначает операцию деления. Он используется для деления одного числа на другое. Например, в выражении «6 ÷ 2» знак «÷» указывает на то, что нужно разделить число 6 на число 2, что дает результат 3.

Что означает знак «=» в математике?

Знак «=» в математике обозначает равенство. Он используется для указания того, что два выражения или значения равны друг другу. Например, в выражении «2 + 3 = 5» знак «=» указывает на то, что сумма чисел 2 и 3 равна числу 5.

Интеграл и производная: понятия и примеры применения

Производная является показателем изменения функции в определенной точке. Математически производная определяется как предел отношения изменения функции к изменению аргумента при бесконечно малом изменении аргумента. Геометрически производная определяет угол касательной к графику функции в данной точке.

Пример применения производной:

Представим, что у нас есть график функции, описывающей движение тела. Изменение скорости тела в момент времени можно определить с помощью производной. Производная позволит нам найти ускорение тела и понять, как оно изменяется во времени.

Интеграл является обратной операцией к производной. Он позволяет находить неизвестные функции по их производной. Интеграл также можно интерпретировать как площадь под графиком функции. Интеграл от функции указывает, сколько площади занимает область между графиком функции и осью абсцисс в заданном интервале.

Пример применения интеграла:

Пусть у нас есть функция, описывающая плотность распределения вероятности случайной величины. Интеграл от этой функции на заданном интервале дает вероятность того, что случайная величина примет значение из этого интервала.

Таким образом, понимание понятий и применение интеграла и производной являются важными для решения различных задач в математике, физике, экономике и других областях науки и техники.

Видео по теме: