Что значит знак математике
Содержимое
- 1 Что значит знак математике
- 1.1 Важность знаков в математике: понимание основных символов и их смысл
- 1.2 Видео по теме:
- 1.3 Арифметические знаки: плюс, минус и их значения
- 1.4 Умножение и деление: знаки умножения и деления и их применение
- 1.5 Вопрос-ответ:
- 1.5.0.1 Что такое знаки в математике и зачем они нужны?
- 1.5.0.2 Какой знак используется для обозначения сложения?
- 1.5.0.3 Какой знак используется для обозначения вычитания?
- 1.5.0.4 Какой знак используется для обозначения умножения?
- 1.5.0.5 Какой знак используется для обозначения деления?
- 1.5.0.6 Какие основные символы используются в математике?
- 1.5.0.7 Какие значения имеют основные знаки в математике?
- 1.6 Знаки сравнения: больше, меньше и равно
- 1.7 Алгебраические знаки: переменные, коэффициенты и выражения
- 1.8 Геометрические знаки: отрезки, углы и фигуры
- 1.9 Статистические знаки: среднее значение, дисперсия и стандартное отклонение
- 1.10 Матричные знаки: определитель, транспонирование и умножение матриц
- 1.11 Логические знаки: и, или, не и их использование в математической логике
Знаки в математике имеют специфическое значение и используются для обозначения различных операций и отношений. Узнайте, какие знаки используются в математике и как они влияют на решение задач.
Математика — это наука, которая использует специальные символы и знаки для обозначения различных математических операций и понятий. Эти символы играют важную роль в математических выражениях и формулах, помогая уточнить значения и отношения между числами и другими математическими объектами.
В данной статье мы рассмотрим основные символы и их обозначения, которые используются в математике. Одним из самых известных символов является плюс (+), который обозначает сложение двух чисел или выражений. Этот символ также используется для обозначения положительных чисел.
Минус (-) является символом вычитания двух чисел или выражений. Он также используется для обозначения отрицательных чисел. Примером использования этого символа может быть выражение «4 — 2», которое означает вычитание числа 2 из числа 4.
Умножение двух чисел обозначается символом «×» или «*», который называется знаком умножения. Например, выражение «2 × 3» означает умножение числа 2 на число 3.
Деление двух чисел обозначается символом «÷» или «/», который называется знаком деления. Например, выражение «6 ÷ 2» означает деление числа 6 на число 2.
В математике также используются другие символы, такие как равно (=), больше (>), меньше (
Знание основных символов и их обозначений в математике является необходимым для понимания и решения различных математических задач. Поэтому, уделите время и усилия для изучения и запоминания этих символов, чтобы быть успешным в изучении и применении математики.
Важность знаков в математике: понимание основных символов и их смысл
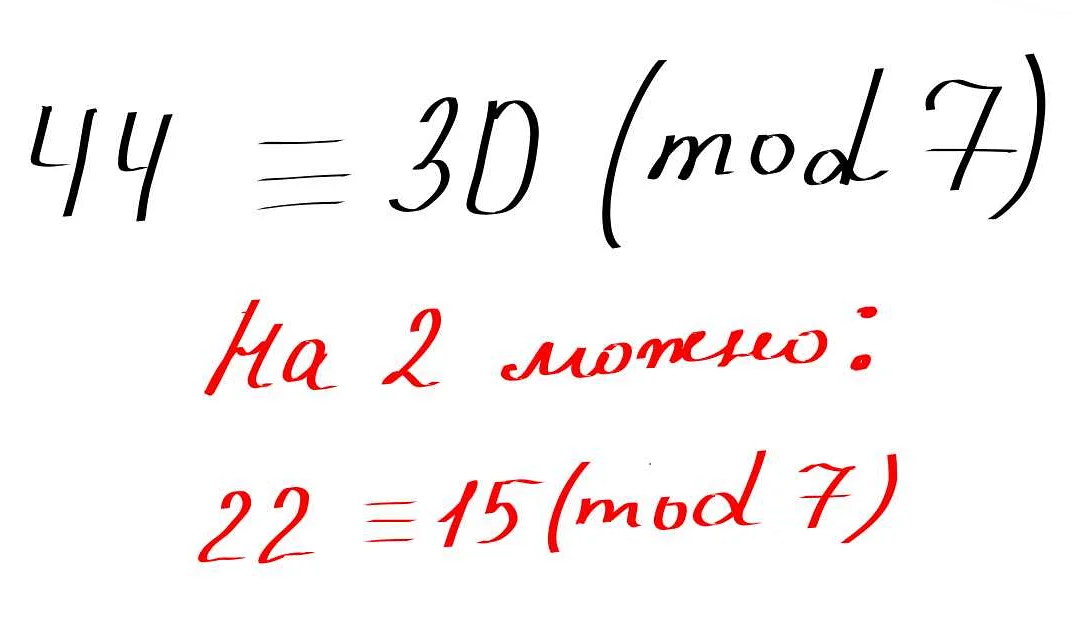
Знаки в математике играют важную роль в передаче информации и обозначении различных математических операций и концепций. Они помогают нам понять смысл и значение выражений, уравнений и формул.
Основные символы в математике имеют свои уникальные значения и смыслы. Например, знак плюс (+) обозначает сложение, а знак минус (-) — вычитание. Знак умножения (×) используется для обозначения умножения, а знак деления (÷) — для обозначения деления.
Другие важные знаки в математике включают знак равенства (=), который указывает на равенство двух выражений или значений. Знак больше (>) и знак меньше (
Кроме того, существуют специальные символы, которые имеют уникальный смысл в математике. Например, знак корня (√) используется для обозначения извлечения квадратного корня из числа. Знаки интеграла (∫) и суммы (∑) используются для обозначения интегралов и сумм соответственно.
Понимание основных символов в математике является необходимым для успешного решения математических задач и формулирования математических выражений и уравнений. Это позволяет нам точно и ясно выражать наши мысли и идеи и обмениваться математической информацией.
Изучение и понимание символов в математике также помогает нам развивать логическое мышление и аналитические навыки. Оно обучает нас видеть связи и взаимосвязи между различными математическими концепциями и применять их в решении сложных задач.
В заключение, знаки в математике являются неотъемлемой частью этой науки и играют важную роль в обозначении и понимании математических операций и концепций. Изучение основных символов и их смысла позволяет нам более эффективно работать с математическими выражениями и уравнениями, развивать логическое мышление и применять математические знания в решении реальных проблем.
Видео по теме:
Арифметические знаки: плюс, минус и их значения
Знак плюс (+) обозначает операцию сложения. Он используется для объединения двух чисел или выражений в одно общее значение. Например, если у нас есть числа 5 и 3, то их сумма будет обозначаться как 5 + 3 = 8. Знак плюс также может использоваться для обозначения положительного числа.
Знак минус (-) обозначает операцию вычитания. Он используется для вычитания одного числа или выражения из другого. Например, если у нас есть число 7 и мы вычитаем из него число 4, то это будет обозначаться как 7 — 4 = 3. Знак минус также может использоваться для обозначения отрицательного числа.
Вместе эти два знака, плюс и минус, образуют основу для выполнения арифметических операций, таких как сложение, вычитание, умножение и деление. Они позволяют нам работать с числами и выполнять различные математические операции.
Изучение и понимание значения арифметических знаков является важной частью основ математики и является основой для дальнейшего изучения более сложных математических концепций.
Умножение и деление: знаки умножения и деления и их применение
Знак умножения также используется для обозначения перемножения переменных или выражений. Например, выражение a × b означает умножение переменной a на переменную b.
Примеры:
4 × 5 = 20
x × y = xy
Деление — это операция, обратная умножению. Она используется для нахождения частного двух чисел. Знаком деления является косая черта (/) или двоеточие (:). Например, выражение 10 ÷ 2 означает деление числа 10 на число 2 и равно 5.
Знак деления также используется для обозначения деления выражений или переменных. Например, выражение ab ÷ c означает деление произведения переменных a и b на переменную c.
Примеры:
12 ÷ 3 = 4
ab ÷ c = ab/c
Знаки умножения и деления являются основными символами в математике и широко используются в различных вычислениях и уравнениях. Они позволяют удобно записывать и решать математические задачи.
Вопрос-ответ:
Что такое знаки в математике и зачем они нужны?
Знаки в математике — это специальные символы, которые используются для обозначения различных математических операций, отношений и условий. Они позволяют нам записывать и передавать математические выражения и идеи более компактно и точно.
Какой знак используется для обозначения сложения?
Для обозначения сложения в математике используется знак «+». Например, если мы хотим сложить два числа, мы записываем их через знак «+». Например, 2 + 3 = 5.
Какой знак используется для обозначения вычитания?
Для обозначения вычитания в математике используется знак «-«. Например, если мы хотим вычесть одно число из другого, мы записываем их через знак «-«. Например, 5 — 2 = 3.
Какой знак используется для обозначения умножения?
Для обозначения умножения в математике используется знак «×» или знак «*», в зависимости от предпочтений автора или используемого стандарта. Например, 2 × 3 = 6 или 2 * 3 = 6.
Какой знак используется для обозначения деления?
Для обозначения деления в математике используется знак «÷» или знак «/», в зависимости от предпочтений автора или используемого стандарта. Например, 6 ÷ 2 = 3 или 6 / 2 = 3.
Какие основные символы используются в математике?
В математике используются различные символы для обозначения разных математических операций, отношений и функций. Некоторые из основных символов включают знаки арифметических операций, такие как плюс (+), минус (-), умножение (×) и деление (÷). Есть также символы для обозначения равенства (=), неравенства (≠), больше (>), меньше (
Какие значения имеют основные знаки в математике?
Основные знаки в математике имеют свои уникальные значения и функции. Например, знак плюс (+) используется для обозначения сложения двух чисел или переменных, минус (-) обозначает вычитание, умножение (×) — умножение, и деление (÷) — деление. Знак равенства (=) обозначает, что два выражения или значения равны, а знак неравенства (≠) указывает на то, что они не равны. Знаки больше (>), меньше (
Знаки сравнения: больше, меньше и равно
В математике существуют особые знаки, которые используются для сравнения чисел и выражений. Эти знаки позволяют установить отношение между двумя величинами и выразить их взаимосвязь.
Один из наиболее распространенных знаков сравнения — это знак «больше». Он обозначается символом «>», и показывает, что одно число является большим, чем другое. Например, если мы имеем два числа: 5 > 3, это означает, что число 5 больше числа 3.
Также в математике есть знак сравнения «меньше», который обозначается символом »
Знак «равно», обозначаемый символом «=», используется для сравнения двух величин и показывает, что они равны. Например, 3 + 2 = 5 означает, что сумма чисел 3 и 2 равна 5.
Знак сравнения «больше или равно» обозначается символами «≥» и показывает, что одно число больше или равно другому. Например, 4 + 1 ≥ 5 означает, что сумма чисел 4 и 1 больше или равна числу 5.
Знак «меньше или равно» обозначается символами «≤» и показывает, что одно число меньше или равно другому. Например, 5 — 2 ≤ 3 означает, что разность чисел 5 и 2 меньше или равна числу 3.
Знание и понимание этих знаков сравнения важно для правильного сравнения чисел и выражений в математике.
Алгебраические знаки: переменные, коэффициенты и выражения
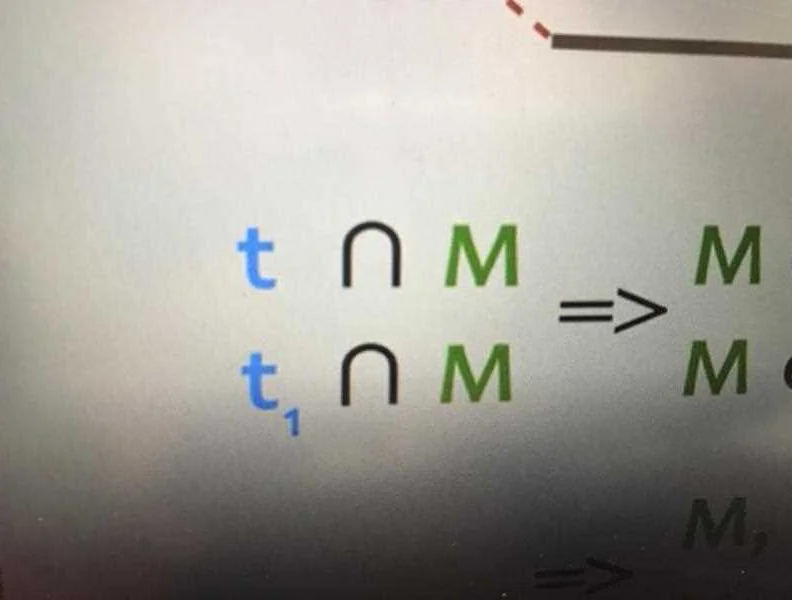
В математике алгебраические знаки играют важную роль при описании и решении алгебраических задач. Они позволяют обозначать переменные, коэффициенты и выражения, которые встречаются в алгебраических формулах и уравнениях.
Переменные — это буквенные обозначения, которые представляют неизвестные значения. Они позволяют работать с неизвестными величинами и изменять их в процессе решения задач. Обычно переменные обозначаются латинскими буквами, такими как x, y, z. Например, в уравнении 2x + 3y = 10 переменные x и y представляют неизвестные значения, которые нужно найти.
Коэффициенты — это числа, которые умножаются на переменные в алгебраических выражениях. Они определяют вес и вклад переменных в общую сумму или результат. Коэффициенты могут быть положительными, отрицательными или нулевыми. Например, в выражении 5x — 2y коэффициенты 5 и -2 определяют вес переменных x и y соответственно.
Выражения — это алгебраические конструкции, состоящие из переменных, коэффициентов и математических операций. Они позволяют записывать математические отношения и проводить операции с переменными и числами. Выражения могут быть простыми или сложными, в зависимости от количества переменных и операций. Например, выражение 3x + 2y — 7 представляет собой сумму трех слагаемых: 3x, 2y и -7.
СимволОбозначениеОписание
| x, y, z | Переменные | Буквенные обозначения неизвестных значений |
| a, b, c | Коэффициенты | Числа, умножаемые на переменные |
| + | Сложение | Операция, объединяющая два выражения или числа |
| — | Вычитание | Операция, вычитающая одно выражение или число из другого |
| * | Умножение | Операция, умножающая два выражения или числа |
| / | Деление | Операция, делящая одно выражение или число на другое |
Алгебраические знаки играют важную роль в решении алгебраических задач. Понимание и правильное использование переменных, коэффициентов и выражений позволяет анализировать и решать сложные алгебраические уравнения и формулы.
Геометрические знаки: отрезки, углы и фигуры
В математике существуют специальные символы и знаки, которые используются для обозначения геометрических фигур и их свойств. Понимание этих знаков позволяет упростить запись и чтение геометрических выражений.
Один из основных геометрических знаков — отрезок, который обозначается двумя точками, например, AB. Отрезок AB представляет собой участок прямой линии между точками A и B.
Еще один важный знак — угол, который обозначается тремя точками, например, ∠ABC. Угол ∠ABC образуется двумя лучами, исходящими из одной точки A и направленными к точкам B и C.
Круг — это геометрическая фигура, которая обозначается символом о. Круг является закрытой кривой линией, состоящей из всех точек, которые равноудалены от одной точки, называемой центром круга.
Прямоугольник — это четырехугольник, у которого все углы прямые. Прямоугольник обозначается символом □.
Треугольник — это трехугольник, который обозначается символом △. Треугольник состоит из трех сторон и трех углов.
Эти знаки и символы используются в математике для обозначения геометрических фигур и упрощения записи выражений. Они помогают наглядно представить геометрические объекты и операции с ними.
Статистические знаки: среднее значение, дисперсия и стандартное отклонение

Среднее значение — это сумма всех значений, деленная на их количество. Оно показывает среднюю величину данных и обозначается символом μ. Например, если у нас есть выборка из 5 чисел: 2, 4, 6, 8, 10, то среднее значение будет равно (2+4+6+8+10)/5 = 6.
Дисперсия — это мера разброса данных относительно их среднего значения. Она показывает, насколько значения в выборке отклоняются от среднего значения. Дисперсия обозначается символом σ2. Для расчета дисперсии необходимо вычислить средний квадрат разности каждого значения среднего значения. Например, для выборки из 5 чисел: 2, 4, 6, 8, 10 среднее значение равно 6. Разность каждого значения среднего значения: (2-6)=-4, (4-6)=-2, (6-6)=0, (8-6)=2, (10-6)=4. Квадрат разностей: (-4)2=16, (-2)2=4, (0)2=0, (2)2=4, (4)2=16. Сумма квадратов разностей: 16+4+0+4+16=40. Дисперсия будет равна 40/5 = 8.
Стандартное отклонение — это квадратный корень из дисперсии. Оно показывает, насколько значения в выборке отклоняются от среднего значения в среднем. Стандартное отклонение обозначается символом σ. Например, для выборки из 5 чисел: 2, 4, 6, 8, 10 с дисперсией равной 8, стандартное отклонение будет равно √8, что примерно равно 2.83.
Знание и понимание этих статистических показателей позволяет проводить анализ данных и делать выводы о их характеристиках. Они широко применяются в различных областях, включая науку, экономику, социологию и другие.
Матричные знаки: определитель, транспонирование и умножение матриц
В математике существует несколько важных знаков, связанных с матрицами. Они позволяют выполнять различные операции над матрицами и получать новые матрицы в результате.
Один из таких знаков — определитель матрицы. Определитель представляет собой число, которое можно вычислить для квадратной матрицы. Он обозначается символом |A| или det(A), где A — матрица. Определитель позволяет определить, является ли матрица вырожденной или обратимой, а также дает информацию о ее свойствах и характеристиках.
Другой важный знак — транспонирование матрицы. Транспонированная матрица получается из исходной путем замены строк на столбцы (и наоборот). Она обозначается символом A^T или A’, где A — исходная матрица. Транспонирование позволяет менять местами строки и столбцы матрицы, что может быть полезным при решении различных задач.
Третий важный знак — умножение матриц. Умножение матриц позволяет получать новую матрицу путем комбинирования элементов исходных матриц. Оно обозначается символом A * B, где A и B — матрицы. Умножение матриц имеет свои особенности и правила, и их соблюдение необходимо для получения корректного результата.
Матричные знаки — определитель, транспонирование и умножение матриц — являются важными инструментами в линейной алгебре и находят применение в различных областях математики, физики, экономики и других наук.
Логические знаки: и, или, не и их использование в математической логике
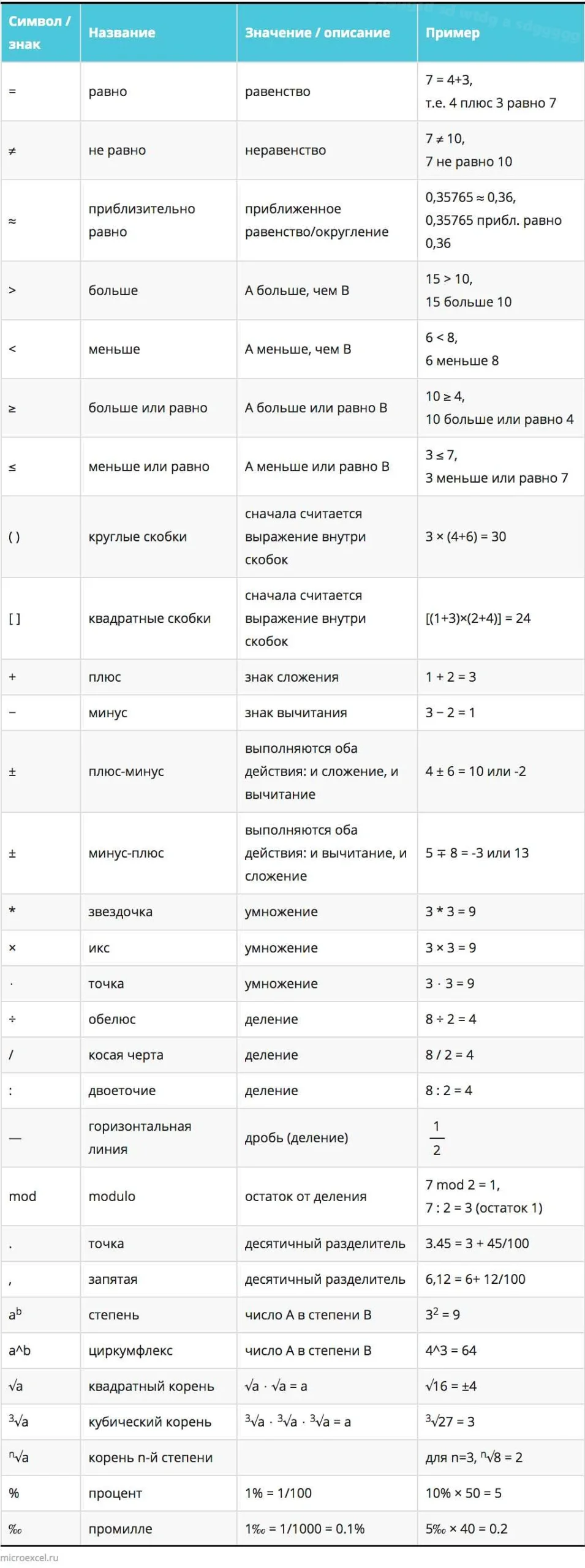
В математической логике существуют особые знаки, которые используются для обозначения логических операций. Они позволяют строить высказывания и проводить рассуждения на основе логических законов.
Один из основных логических знаков — «и». Он обозначается символом «&» или символом «*», и указывает на то, что оба высказывания, между которыми он стоит, должны быть истинными, чтобы итоговое высказывание было истинным. Например, если утверждение А — «Сегодня идет дождь», а утверждение В — «Я беру зонтик», то их объединение с помощью логического знака «и» будет звучать так: «Сегодня идет дождь и я беру зонтик».
Следующий логический знак — «или». Он обозначается символом «∨» или символом «+», и указывает на то, что хотя бы одно из высказываний, между которыми он стоит, должно быть истинным, чтобы итоговое высказывание было истинным. Например, если утверждение А — «Сегодня идет дождь», а утверждение В — «Я не беру зонтик», то их объединение с помощью логического знака «или» будет звучать так: «Сегодня идет дождь или я не беру зонтик».
Третий логический знак — «не». Он обозначается символом «¬» или символом «~», и указывает на то, что высказывание, после которого он стоит, должно быть ложным, чтобы итоговое высказывание было истинным. Например, если утверждение А — «Сегодня идет дождь», то отрицанием этого высказывания будет «Сегодня не идет дождь».
Логические знаки «и», «или» и «не» позволяют построить сложные высказывания и проводить логические рассуждения на основе математической логики. Они являются основой для многих областей математики, информатики и философии.
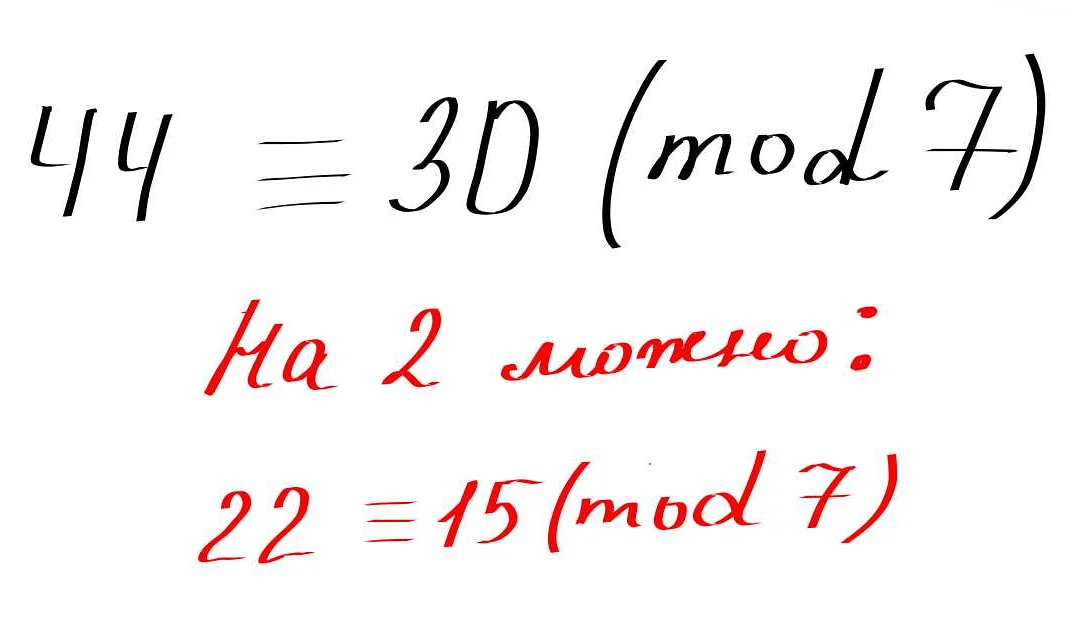


С большим интересом прочитал статью о значениях знаков в математике. Действительно, знаки играют огромную роль в этой науке, помогая нам понять и записать математические операции. Очень важно знать основные символы и их обозначения, чтобы правильно интерпретировать математическую информацию. Например, знак «+» используется для обозначения сложения, а знак «−» для вычитания. Знак умножения «×» и деления «÷» также необходимы для записи математических операций. Конечно, не обойтись без символа равенства «=», который показывает, что два выражения имеют одинаковое значение. Также стоит отметить символы больше «>» и меньше «
Эта статья очень полезна и интересна. Математика всегда была для меня сложной дисциплиной, но благодаря этой статье я смог разобраться в основных символах и их обозначениях. Теперь я легко могу расшифровывать формулы и уравнения. Например, теперь я знаю, что символ «+» означает сложение, а символ «-» — вычитание. Также я узнал, что знак умножения обозначается как «*», а знак деления — «/». Это действительно полезная информация, которая позволяет мне лучше понимать и использовать математику в повседневной жизни. Спасибо автору за такую полезную статью!
Статья очень полезна и информативна! Я всегда интересовалась математикой, но никогда не задумывалась о значении всех этих символов. Теперь я понимаю, что каждый знак имеет свое специальное значение и помогает нам в решении математических задач. Например, знак «плюс» означает сложение, а «минус» — вычитание. А что же значит знак «равно»? Он указывает на то, что два выражения или числа равны друг другу. Интересно, какой символ обозначает умножение? Ах, понятно, это знак «умножить». Теперь, когда я знаю значение всех этих знаков, я смогу лучше понимать математические задачи и решать их более эффективно. Спасибо за такую интересную статью!