Что первое в математике умножение или деление

Статья рассматривает вопрос о том, что первое в математике — умножение или деление. Разъяснение основных принципов и порядка выполнения этих операций.

В мире математики существует вечная дискуссия о том, что является первым — умножение или деление. Оба эти математические операции являются одними из основных, и каждая из них играет важную роль в решении различных задач. Однако, чтобы понять, что на самом деле появилось первым, необходимо взглянуть на историю развития математики.

Умножение, как математическая операция, появилось раньше, чем деление. Оно было открыто и изучено древними цивилизациями, такими, как Древний Египет и Месопотамия, которые использовали умножение для решения задач, связанных с торговлей, архитектурой и другими областями. Умножение позволяет объединять несколько одинаковых чисел в одно и выражать их через умножение на коэффициент.

С другой стороны, деление является обратной операцией к умножению. Понятие деления появилось позже и стало активно развиваться в Древней Греции. Деление позволяет разбивать число на равные части или определять количество групп, которые можно получить из заданного числа. Оно играет важную роль в различных областях, таких как физика, экономика и статистика.

Таким образом, умножение появилось раньше, чем деление, и оба этих понятия являются важными в математике. Они взаимосвязаны и позволяют решать широкий спектр задач. Но без умножения не было бы деления, и наоборот. Оба этих понятия сочетаются вместе, чтобы помочь нам лучше понимать мир чисел и решать сложные задачи.

Что важнее в математике: умножение или деление?

Умножение — это операция, которая используется для повторения одного и того же числа несколько раз или для нахождения произведения двух или более чисел. Умножение позволяет быстро вычислить результат, когда нужно прибавить одно и то же число несколько раз.

Например, если у нас есть 5 яблок, и мы хотим узнать, сколько яблок будет, если умножить их на 3, мы можем использовать умножение: 5 * 3 = 15. Таким образом, умножение позволяет нам быстро найти общее количество яблок.

Деление — это операция, обратная к умножению. Она используется для разделения одного числа на другое или для нахождения частного двух чисел. Деление позволяет нам распределить количество на равные части или узнать, сколько раз можно разделить одно число на другое.

Например, если у нас есть 15 яблок и мы хотим разделить их на 3 равные группы, мы можем использовать деление: 15 / 3 = 5. Таким образом, деление позволяет нам равномерно распределить яблоки между группами.

Обе операции, умножение и деление, важны и необходимы в математике. Они взаимосвязаны и используются вместе для решения различных задач. Например, если нам нужно найти значение неизвестной переменной в уравнении, мы можем использовать как умножение, так и деление.

Таким образом, нельзя сказать, что одна операция важнее другой в математике. Они оба играют важную роль и помогают нам решать различные задачи, а их значимость зависит от конкретной ситуации и поставленной задачи.

Видео по теме:

Роль умножения и деления в математике

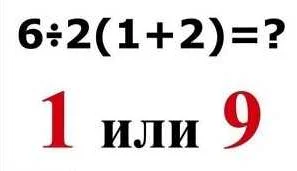
Умножение в математике используется для увеличения значения числа. Оно позволяет складывать множество одинаковых чисел, таким образом упрощая вычисления. Например, умножение используется для нахождения площади прямоугольника, объема параллелепипеда или для решения задачи о равномерном движении.

Деление, в свою очередь, выполняет обратную функцию умножению. Оно позволяет разделить одно число на другое и найти результат этой операции. Деление используется для распределения объектов или количества на равные части, для нахождения среднего значения или вычисления процента.

Оба действия, умножение и деление, тесно связаны и взаимодополняют друг друга. Знание и понимание этих операций является неотъемлемой частью развития математических навыков и способствует глубокому пониманию числовых отношений.

Итак, умножение и деление играют важную роль в математике, предоставляя нам возможность производить вычисления, находить решения задач и применять математические концепции в реальной жизни.

Значение умножения для решения задач

Умножение играет важную роль в многих областях нашей жизни. Например, в финансовой сфере, умножение используется для расчета процентов, суммы вклада или кредита. В науке умножение помогает нам проводить различные эксперименты и расчеты, а в строительстве — определить площадь поверхности или объем объекта.

Однако наиболее частым применением умножения является решение задач на пропорциональность и соотношение. Например, при расчете стоимости товаров по единичной цене или при определении времени, которое требуется для преодоления расстояния с определенной скоростью.

Умножение также является основой для изучения других математических операций, таких как деление, возведение в степень и извлечение корня. Без понимания и правильного применения умножения, невозможно эффективно решать сложные математические задачи.

В заключение, умножение играет важную роль в нашей повседневной жизни и в математике. Оно помогает нам проводить расчеты, решать задачи и справляться с различными математическими операциями. Поэтому понимание и умение применять умножение является необходимым навыком для успешного решения математических задач и для развития логического мышления.

Вопрос-ответ:

Какое из математических действий — умножение или деление — является первым?

Первым из математических действий является умножение.

Почему умножение считается первым математическим действием?

Умножение считается первым математическим действием, потому что оно является базовым для понимания деления. Чтобы выполнить деление, необходимо знать таблицу умножения и уметь умножать числа.

Какое значение имеет умножение в математике?

Умножение — это операция комбинирования двух или более чисел, которая позволяет найти их произведение. Оно имеет большое значение в математике и используется в различных областях, таких как алгебра, геометрия, физика и экономика.

Почему деление считается вторым математическим действием?

Деление считается вторым математическим действием, потому что оно является обратной операцией умножения. Когда мы делим одно число на другое, мы ищем количество раз, которое одно число содержится в другом.

Как умножение и деление связаны между собой?

Умножение и деление связаны между собой, так как они являются взаимообратными операциями. Если мы умножим одно число на другое, а затем разделим полученный результат на первое число, мы получим исходное второе число. Таким образом, деление можно рассматривать как «разделение» умножения.

Что первое в математике: умножение или деление?

В математике, умножение и деление являются двумя основными операциями. Однако, умножение считается первой операцией, так как оно основано на повторении сложения. Деление же является обратной операцией к умножению и используется для разделения общей суммы на равные части.

Какая операция в математике важнее: умножение или деление?

Умножение и деление оба являются важными операциями в математике и выполняют разные функции. Умножение используется для нахождения общего значения при повторении сложения, а деление — для разделения общего значения на равные части. Важность каждой операции зависит от конкретной задачи или контекста, в котором они используются.

Примеры употребления умножения в повседневной жизни

1. При покупке продуктов в супермаркете, мы часто сталкиваемся с умножением. Например, если фрукты стоят 50 рублей за килограмм, а мы хотим купить 2 килограмма, то мы можем рассчитать общую стоимость путем умножения 50 на 2, что даст нам 100 рублей.
2. В строительстве умножение используется для расчета площади поверхности. Например, если у нас есть комната шириной 5 метров и длиной 3 метра, то мы можем найти площадь комнаты, умножив эти два числа: 5 * 3 = 15 квадратных метров.
3. При расчете времени пути, умножение также может пригодиться. Например, если мы едем на машине со скоростью 60 километров в час и хотим узнать, сколько времени займет поездка на расстояние 120 километров, мы можем разделить расстояние на скорость: 120 / 60 = 2 часа.
4. В финансовой сфере умножение используется для расчета процентов. Например, если у нас есть сумма вклада 1000 рублей, а процент составляет 5%, то мы можем найти сумму процентов путем умножения: 1000 * 0.05 = 50 рублей.

Это лишь некоторые примеры использования умножения в повседневной жизни. Однако, он широко применяется во многих других ситуациях, и его понимание является важным навыком для эффективного функционирования в современном мире.

Влияние умножения на развитие логического мышления

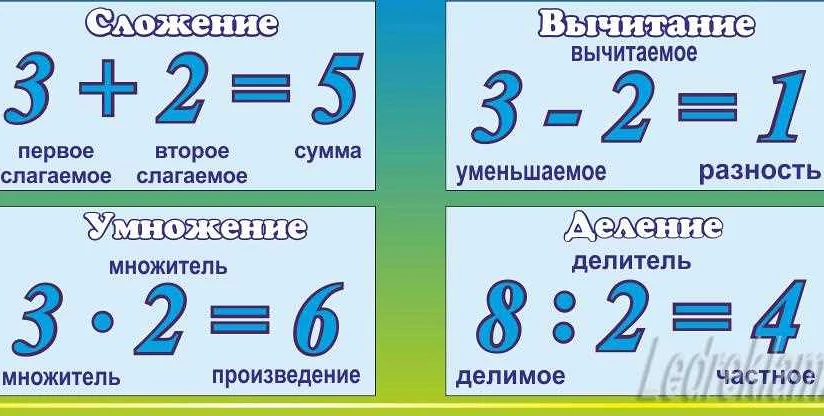
Основная задача умножения состоит в том, чтобы найти произведение двух или более чисел. Для этого необходимо разбить задачу на более простые шаги и правильно применять правила умножения. Это требует от человека умения анализировать, находить закономерности и применять их в дальнейших расчетах.

Умножение также помогает развивать навыки умственного расчета. При умножении чисел в уме необходимо использовать логические способности для быстрого нахождения правильного ответа. Это тренирует мозг и способствует развитию логического мышления.

Кроме того, умножение учат применять в реальных жизненных ситуациях, таких как покупки, расчеты времени, конвертация единиц измерения и т. д. Знание умножения позволяет быстро и точно производить математические операции, что является важным навыком для решения повседневных задач.

Таким образом, умножение играет важную роль в развитии логического мышления у людей. Оно требует анализа, применения правил и развивает умственные способности, необходимые для успешного решения математических задач и применения их в реальной жизни.

Значение деления в математике

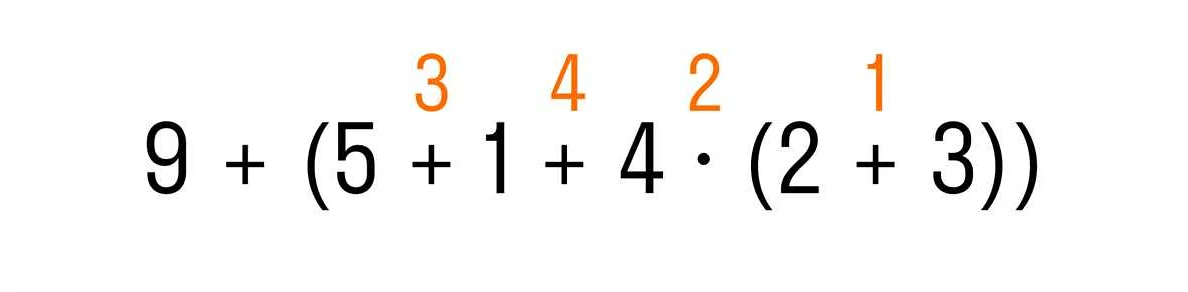
Знак деления обозначается горизонтальной чертой: /. Результат деления называется частным, а числа, которые делятся и на которые делится, называются делимым и делителем соответственно.

Деление можно представить как обратную операцию к умножению. Если мы знаем результат умножения двух чисел и одно из этих чисел, то мы можем найти второе число путем деления.

Пример:

Для чисел 12 и 3, результатом умножения является число 36. Если мы знаем, что одно из чисел равно 12, то мы можем найти второе число, разделив 36 на 12. В данном случае, результатом деления будет число 3.

Деление также позволяет решать задачи на поиск неизвестного числа. Если мы знаем результат деления и одно из чисел, то мы можем найти второе число, применив обратную операцию.

Пример:

Если результатом деления двух чисел является число 4, а одно из чисел равно 12, мы можем найти второе число, разделив 12 на 4. В данном случае, результатом деления будет число 3.

Таким образом, деление является важной операцией в математике, которая позволяет находить результаты умножения и решать задачи на поиск неизвестного числа.

Примеры использования деления для решения задач

1. Распределение ресурсов: Предположим, у вас есть 12 яблок и 3 детей. Вы можете разделить яблоки поровну между детьми, используя деление. В этом случае, если вы разделите 12 яблок на 3 детей, каждый ребенок получит 4 яблока.
2. Расчет среднего значения: Представим, что у вас есть список чисел, например: 5, 10, 15, 20. Чтобы найти среднее значение этих чисел, вы можете сложить их и разделить на количество чисел в списке. В данном случае, если вы сложите 5 + 10 + 15 + 20, получите 50, и разделите на 4 числа, получите среднее значение 12.5.
3. Расчет скорости: Предположим, что вы проехали 300 километров за 5 часов. Чтобы найти вашу среднюю скорость, вы можете разделить пройденное расстояние на время. В данном случае, если вы разделите 300 км на 5 часов, получите среднюю скорость 60 км/ч.
4. Расчет стоимости на человека: Представим, что вы организуете вечеринку и заказываете пиццу. Если стоимость пиццы составляет 1200 рублей, а вас 6 человек, вы можете использовать деление, чтобы узнать стоимость на каждого. В этом случае, если вы разделите 1200 рублей на 6 человек, получите, что каждый должен заплатить 200 рублей.

Таким образом, деление является мощным инструментом для решения различных задач в математике и в реальной жизни.

Как деление помогает в понимании пропорций и отношений

Пропорции являются важным элементом математического анализа и используются в различных областях знания, таких как физика, экономика, геометрия и другие. Деление помогает определить, как одно значение относится к другому и позволяет установить соответствующие пропорции.

Например, при решении задачи на расчет скорости можно использовать деление для определения отношения пройденного пути к затраченному времени. Также, при расчете долей и процентов, деление позволяет определить соотношение между частью и целым.

Основополагающее понятие пропорций и отношений также важно в повседневной жизни. Например, при покупке продуктов в магазине, деление используется для рассчета цены за единицу товара или для определения соотношения количества продукта к его стоимости.

Таким образом, деление помогает в понимании пропорций и отношений и является неотъемлемой частью математической грамотности. Оно позволяет анализировать и интерпретировать данные, а также применять полученные знания в повседневной жизни и различных областях науки.