Что самое сложное в высшей математике

Высшая математика представляет собой сложную область знаний, где самое сложное заключается в абстрактности и сложности математических концепций, формул и доказательств. Она требует глубокого понимания алгебры, анализа, теории вероятности и других разделов математики, а также умения абстрактно мыслить и логически рассуждать. Изучение высшей математики требует много времени, упорства и терпения, но оно позволяет решать сложные проблемы, разрабатывать новые теории и применять математические методы в различных областях науки и технологий.

Высшая математика является одной из наиболее сложных и абстрактных наук. Понимание ее основных концепций и методов требует от исследователей глубокого аналитического мышления и творческого подхода. Возможно, самое сложное в высшей математике — это абстрактность предмета и его задач.

Математика старается абстрагироваться от реального мира и работать с абстрактными объектами и конструкциями. В высшей математике, например, мы можем говорить о бесконечных множествах, о функциях, которые не имеют геометрической интерпретации, и о пространствах, которые мы не можем представить в трехмерном мире. Это требует от математиков способности мыслить абстрактно и видеть связи между различными объектами и концепциями.

Кроме того, задачи в высшей математике могут быть чрезвычайно сложными. Они могут требовать применения различных теорем, методов и алгоритмов, а также умения применять их в различных контекстах. Одна задача может потребовать комбинаторного анализа, другая — доказательства сложной теоремы, а третья — применения математического моделирования для решения реальной проблемы. Это делает высшую математику сложным и многосторонним предметом, требующим от исследователей глубокого знания и понимания различных областей и методов математики.

Абстрактность в высшей математике

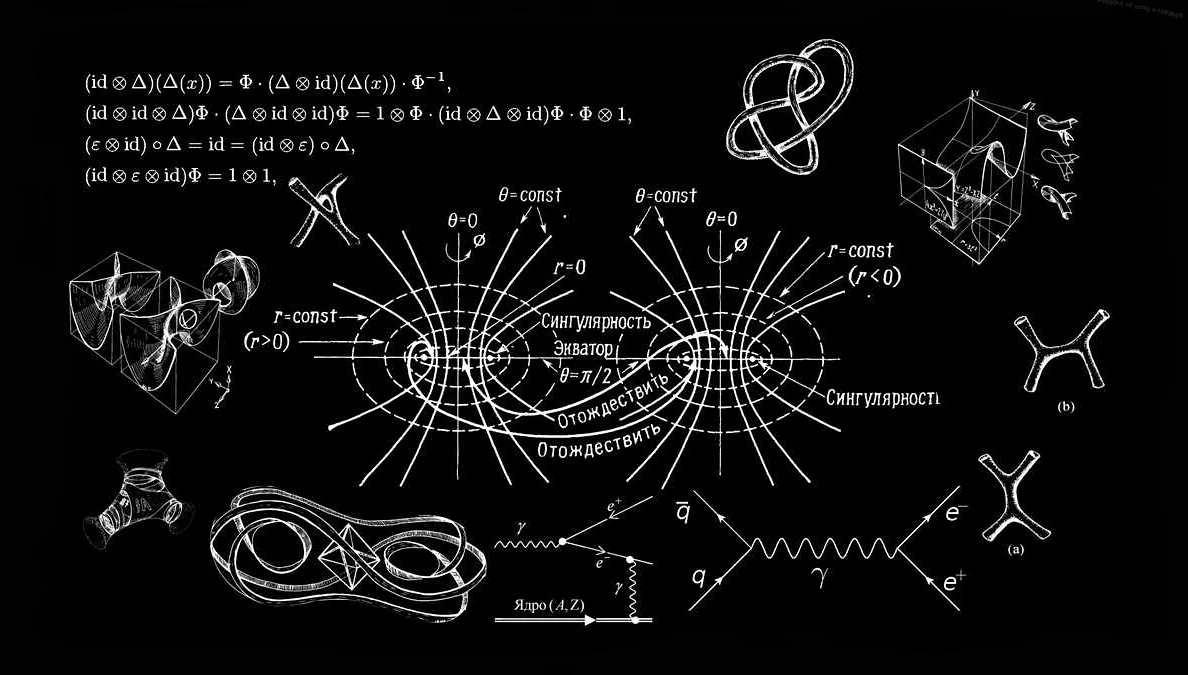
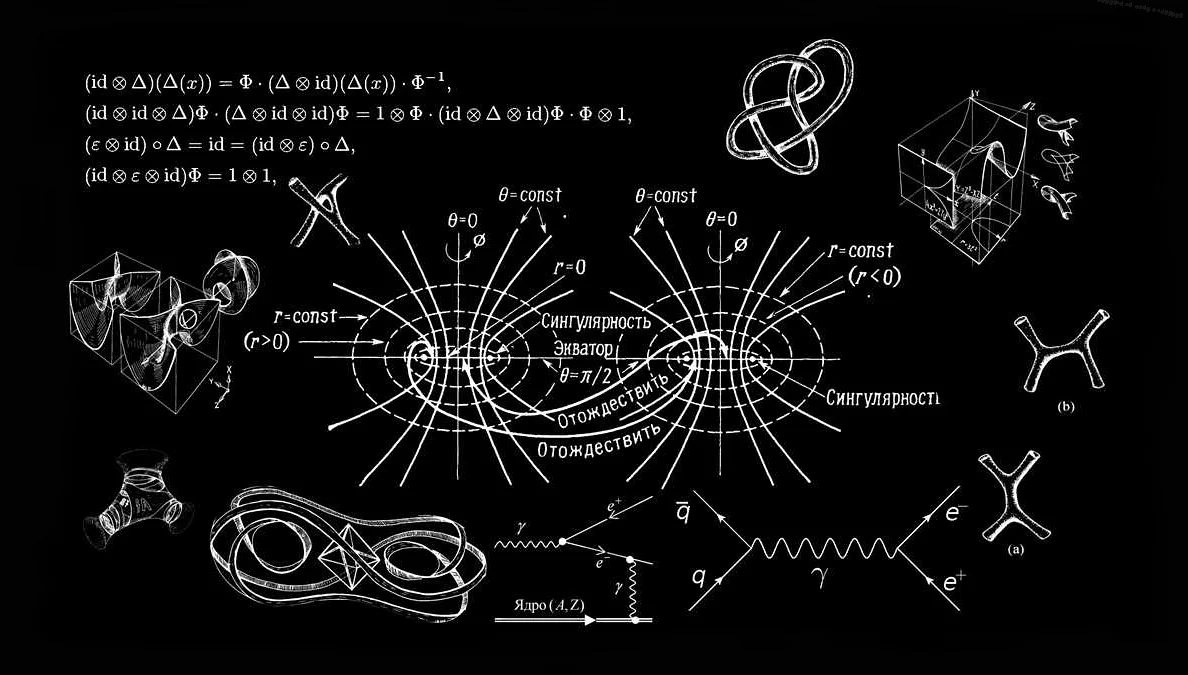
Одним из примеров абстрактности в высшей математике является использование символов и формул для представления математических концепций. Это позволяет математикам работать с абстрактными объектами, такими как числа, функции, векторы и множества, без привязки к конкретным значениям или ситуациям.

Абстрактность также проявляется в самом способе мышления математиков. Они стремятся абстрагироваться от конкретных примеров и искать общие закономерности и свойства. Это позволяет им создавать обобщенные модели и теории, которые могут быть применены для решения различных задач и проблем.

Однако абстрактность в высшей математике может быть сложной для понимания и применения. Многие концепции и теории требуют глубокого понимания математических принципов и логики. Иногда математические объекты и операции могут быть абстрактными до такой степени, что их связь с реальными ситуациями может быть неочевидной.

Однако абстрактность в высшей математике является неотъемлемой частью ее развития и прогресса. Благодаря абстрактным концепциям и методам, математики могут создавать новые теории, решать сложные задачи и применять свои знания в различных областях науки и технологий.

Сложность и понимание

Абстрактность математических понятий и формул может вызвать затруднения в их понимании. Многие студенты сталкиваются с трудностями при переходе от конкретных примеров к абстрактным рассуждениям. Однако, с достаточным временем и упорством, абстрактность математики может быть понята и освоена.

Важно понимать, что сложность задач в высшей математике не является препятствием, а скорее вызовом для развития своих умственных навыков. Необходимо находить новые подходы к решению сложных задач и не бояться пробовать нестандартные методы. Именно в этом заключается основная сложность – в развитии интуиции и креативного мышления.

Чтобы успешно справиться с сложностью математических задач, необходимо также развивать систематический подход к изучению материала. Важно уделять достаточное количество времени для повторения и закрепления изученного, а также постоянно практиковаться в решении различных задач.

В заключение, сложность высшей математики не должна отпугивать студентов, а должна быть рассмотрена как вызов для развития умственных навыков и интуиции. С достаточным пониманием и упорством, сложность может быть преодолена, и математика станет увлекательным и уважаемым предметом.

Абстрактные понятия и символы

Высшая математика известна своей абстрактностью и использованием сложных символов. Однако, именно эти абстрактные понятия и символы делают математику такой мощной и универсальной наукой.

Абстрактные понятия в математике представляют собой идеи или концепции, которые не связаны с конкретными объектами или ситуациями в реальном мире. Они позволяют нам анализировать и описывать различные структуры и отношения между ними. Например, понятие «множество» является абстрактным, так как оно не имеет конкретного физического представления. Однако, оно позволяет нам оперировать с группами объектов и исследовать их свойства.

Символы в математике используются для представления абстрактных понятий и математических операций. Они позволяют нам записывать и передавать информацию компактно и точно. Например, символы «+», «-«, «*» и «/» используются для обозначения арифметических операций сложения, вычитания, умножения и деления соответственно. Символы, такие как «=», «>», »

Использование абстрактных понятий и символов в высшей математике требует от студентов исключительной внимательности и точности. Каждый символ или понятие имеет свою строгое определение и правила использования. Даже малейшая ошибка или неправильное понимание может привести к неправильному решению задачи или получению неверных результатов.

Однако, с практикой и опытом студенты становятся более уверенными в работе с абстрактными понятиями и символами. Они начинают видеть связи между различными математическими объектами и понимать, как они взаимодействуют между собой. Это позволяет им решать более сложные задачи и создавать новые математические концепции и теории.

Таким образом, абстрактные понятия и символы являются неотъемлемой частью высшей математики. Они позволяют нам описывать и анализировать сложные структуры и отношения, а также решать сложные задачи. С их помощью математика становится мощным инструментом для исследования мира и построения новых знаний.

Сложность задач в высшей математике

Задачи в высшей математике требуют от математика глубокого понимания теории и способности анализировать и решать сложные проблемы. Они часто имеют множество неизвестных и требуют применения разнообразных методов и подходов.

Сложность задач в высшей математике также заключается в их абстрактности. Они могут быть сформулированы на языке формул, символов и операций, что делает их непонятными для обычного человека. Математик должен быть способен перевести абстрактные задачи в понятные термины, чтобы определить их решение.

Еще одной сложностью задач в высшей математике является их интуитивный характер. Некоторые задачи могут требовать от математика нестандартного мышления и интуитивного подхода к решению. Это означает, что решение задачи не всегда может быть получено путем простого применения известных формул и методов.

Таким образом, сложность задач в высшей математике проистекает из их абстрактности, множества неизвестных, требования интуитивного мышления и глубокого понимания теории. Однако, это именно сложность задач делает высшую математику такой увлекательной и интересной для математиков.

Разнообразие проблем

Математические проблемы могут быть абстрактными и сложными, требующими глубокого понимания основных концепций и теорий. Однако, помимо этого, они также могут быть разнообразными по своей сути и прикладным направлением.

Например, в высшей математике изучаются проблемы, связанные с алгеброй, геометрией, анализом и теорией вероятностей. Каждая из этих областей имеет свои особенности и сложности, которые требуют глубокого анализа и решения.

Также в высшей математике изучаются проблемы, связанные с оптимизацией, моделированием и теорией графов. Эти проблемы имеют практическую значимость и широкое применение в различных областях, таких как экономика, физика и информатика.

Разнообразие проблем в высшей математике требует от ученых и студентов глубокого знания и понимания различных областей математики. Оно также предоставляет возможность для развития и открытия новых методов и подходов к решению сложных математических задач.

Вычислительная сложность

Одним из основных факторов, определяющих вычислительную сложность, является абстрактность задачи. Чем более сложная и абстрактная задача, тем больше времени и ресурсов потребуется для ее решения.

Сложность задачи также может зависеть от используемого алгоритма. Некоторые алгоритмы могут быть более эффективными и требовать меньшего количества вычислительных ресурсов, чем другие. Однако, даже самые эффективные алгоритмы могут иметь высокую вычислительную сложность при работе с очень большими объемами данных или при выполнении сложных операций.

Вычислительная сложность важна не только для математических задач, но и для практических применений, таких как оптимизация процессов, анализ данных, машинное обучение и т. д. Понимание и оценка вычислительной сложности помогает выбирать наиболее эффективные алгоритмы и ресурсы для решения задачи.

Применение математики в реальной жизни

Применение математики можно наблюдать в различных сферах нашей жизни. Например, она играет важную роль в финансовой сфере. Математические модели используются для прогнозирования финансовых рынков, определения рисков и создания стратегий инвестирования. Точные расчеты и статистические методы позволяют принимать обоснованные решения и управлять финансовыми активами.

Математика также широко применяется в технике и инженерии. Она помогает разработать и оптимизировать сложные системы и процессы. Например, при проектировании зданий и мостов математические расчеты позволяют определить необходимую прочность материалов и оптимальную форму конструкции. В авиации математика используется для моделирования полета и разработки авиационных систем.

Также математика находит применение в информационных технологиях. Криптография, компьютерная графика, алгоритмы искусственного интеллекта — все эти области тесно связаны с математикой. Криптографические алгоритмы обеспечивают безопасность информации, а компьютерная графика использует математические модели для создания реалистичных изображений.

Применение математики можно найти и в медицине, географии, экологии, социологии и многих других научных областях. Математические модели и статистические методы позволяют анализировать и предсказывать различные явления, а также оптимизировать процессы и принимать обоснованные решения.

Таким образом, математика, несмотря на свою абстрактность и сложность, имеет практическую значимость и широкое применение в реальной жизни. Она является мощным инструментом для решения различных задач и помогает нам лучше понимать и контролировать мир вокруг нас.

Видео по теме:

Вопрос-ответ:

Чем отличается высшая математика от обычной?

Высшая математика — это раздел математики, который изучает абстрактные и сложные математические структуры и их свойства. Она отличается от обычной математики тем, что включает в себя более сложные и абстрактные концепции, такие как теория множеств, теория вероятности, математическая логика и др.

Почему высшая математика считается сложной?

Высшая математика считается сложной, потому что она требует абстрактного мышления и умения решать сложные математические задачи. Она часто использует новые и неочевидные подходы к решению проблем, и для ее изучения необходимо иметь хорошую математическую подготовку и умение логически мыслить.

Какие основные принципы и концепции используются в высшей математике?

В высшей математике используются такие основные принципы и концепции, как теория множеств, алгебра, математический анализ, дифференциальные уравнения, теория вероятности, математическая логика и теория графов. Эти концепции являются основой для изучения более сложных математических структур и задач.

Можно ли изучать высшую математику без специального образования?

Изучение высшей математики без специального образования может быть сложным, так как она требует знания и понимания базовых математических концепций. Однако, с достаточным уровнем самообучения и упорством, можно освоить основы высшей математики и изучать более сложные темы. Существуют также курсы и учебники, которые помогут в изучении данной области.

Прогнозирование и моделирование

Прогнозирование заключается в предсказании будущих значений переменных на основе имеющихся данных. Для этого используются различные методы, такие как статистические модели, регрессионный анализ, машинное обучение и другие. Прогнозирование широко применяется в различных областях, включая экономику, финансы, маркетинг, климатологию и т.д.

Моделирование, в свою очередь, представляет собой создание математических моделей, которые описывают поведение системы или явления. Модель может быть аналитической, когда она описывается аналитическими уравнениями, или численной, когда используются численные методы для решения уравнений. Моделирование позволяет анализировать и прогнозировать сложные системы, такие как погодные условия, физические процессы, экономические системы и другие.

Одной из основных сложностей прогнозирования и моделирования является абстрактность и сложность задач. В высшей математике используются абстрактные понятия, такие как функции, уравнения, графы, которые не всегда имеют непосредственное отображение в реальных объектах и явлениях. Кроме того, моделирование и прогнозирование требуют тщательного анализа и обработки больших объемов данных, а также выбора подходящих методов и моделей.

В целом, прогнозирование и моделирование являются важными инструментами, которые позволяют понять и предсказывать сложные системы и явления. Они играют ключевую роль в различных областях науки и промышленности, помогая принимать обоснованные решения и разрабатывать эффективные стратегии.

Шифрование и безопасность

Шифрование – это процесс преобразования данных таким образом, чтобы они стали непонятными для посторонних лиц. Шифрование используется для защиты информации от несанкционированного доступа и обеспечения конфиденциальности. Оно позволяет передавать данные по интернету или хранить их на компьютере в зашифрованном виде, таким образом предотвращая возможность прослушивания или взлома.

Существуют различные методы шифрования, каждый из которых имеет свои особенности и степень сложности. Одним из самых распространенных методов шифрования является симметричное шифрование, где для шифрования и дешифрования используется один и тот же ключ. Другим популярным методом является асимметричное шифрование, где используются два разных ключа – публичный и приватный.

Шифрование имеет огромное значение в таких областях как банковское дело, медицина, военная техника, электронная коммерция и другие. Оно помогает защитить личные данные, финансовые счета, коммерческую информацию и другую важную информацию от несанкционированного доступа. Благодаря шифрованию, можно быть уверенным в сохранности своих данных и обеспечить безопасность своей информации.

Тем не менее, разработка и использование современных криптографических алгоритмов является сложным и трудоемким процессом. Криптографы и математики занимаются разработкой новых алгоритмов и методов шифрования, а также их анализом и усовершенствованием. Целью этих усилий является создание надежных систем шифрования, которые были бы устойчивы к взлому и обеспечивали бы высокую степень безопасности.

Выводы:

Шифрование играет важную роль в обеспечении безопасности информации. Оно позволяет защитить данные от несанкционированного доступа и обеспечить конфиденциальность. Современные методы шифрования являются сложными и требуют математических знаний и навыков. Разработка и использование надежных криптографических алгоритмов является активной областью исследований, направленных на повышение уровня безопасности информации.