Что такое 5 часть в математике

Пятая часть в математике — это одна пятая от целого числа или доли, которая представляет собой 20%. Узнайте, как вычислять пятую часть от числа и как использовать ее в различных задачах и расчетах.

5 часть в математике – это одна из основных операций для деления чисел. Когда мы делим одно число на другое, получаем результат, который называется частным. Если при делении нацело получается частное, равное целому числу, то это и есть 5 часть.

5 часть представляет собой операцию, которая позволяет разделить одно число на другое и получить на выходе результат, который будет равен 5. Иными словами, 5 часть – это деление числа на 5 без остатка. Например, 15 делится на 5 без остатка и равно 3.

Пример: 15 / 5 = 3

Таким образом, 5 часть в математике – это операция, которая помогает нам разделить число на 5 и получить результат без остатка. Это важное понятие, которое используется в различных областях математики, физики, экономики и других науках.

Основные понятия

Чтобы выразить число пятой части в математической форме, мы пишем дробь 1/5. Здесь числитель равен 1, что означает, что мы рассматриваем одну пятую часть, а знаменатель равен 5, что означает, что целое число было разделено на пять равных частей.

Примеры чисел, равных пятой части:

• Если у нас есть 10 яблок и мы берем одну пятую часть, то мы берем 2 яблока (10/5 = 2).
• Если у нас есть 15 долларов и мы берем одну пятую часть, то мы берем 3 доллара (15/5 = 3).
• Если у нас есть 20 минут и мы берем одну пятую часть, то мы берем 4 минуты (20/5 = 4).

Таким образом, понятие «5 часть» в математике означает, что мы рассматриваем одну пятую часть от целого числа, которое было разделено на пять равных частей.

Примеры использования

Пятая часть в математике может быть использована в различных областях и задачах. Рассмотрим несколько примеров:

1. Проценты: При расчете процентов, пятая часть может быть использована для определения 5% от числа. Например, 5% от 100 равно 5.

2. Дроби: В математике, пятая часть может быть представлена в виде дроби 1/5. Например, 1/5 + 1/5 + 1/5 + 1/5 + 1/5 = 1.

3. Коэффициенты: Пятая часть может быть использована как коэффициент в уравнениях и формулах. Например, если у нас есть уравнение 5x = 20, то пятая часть, равная 5, может быть использована для определения значения переменной x.

4. Вероятность: Вероятность события может быть выражена с использованием пятой части. Например, если у нас есть 5 одинаковых монет и мы бросаем их одновременно, вероятность выпадения одной стороны монеты будет равна 1/5.

Это только несколько примеров использования пятой части в математике. Она широко применяется в различных областях и задачах для упрощения вычислений и описания отношений.

Практическое применение

Например, если у вас есть число 100, и вы хотите найти 5% этого числа, вы можете использовать 5 часть. Для этого нужно умножить число на 5 часть (0,05), чтобы получить результат.

Также 5 часть можно использовать для решения различных задач, связанных с долями и процентами. Например, если у вас есть группа людей и вы хотите выяснить, сколько процентов от общего числа составляет определенная группа, вы можете использовать 5 часть, чтобы вычислить это значение.

Кроме того, 5 часть часто используется в финансовых расчетах, таких как расчет процентных ставок, скидок и налогов.

В общем, понимание и использование 5 части в математике является важным навыком и может быть полезным во многих сферах жизни, где требуются расчеты процентов и долей.

Значение в математике

В математике понятие «значение» относится к результату вычисления или оценке выражения, функции или переменной. Значение представляет собой числовую величину или некоторое другое значение, которое можно получить путем применения определенных правил или операций.

Значение может быть абсолютным или относительным. Абсолютное значение представляет собой числовую величину без учета направления или контекста. Например, абсолютное значение числа -5 равно 5. Относительное значение зависит от контекста и может быть определено в отношении других значений или точек отсчета.

В математических выражениях или функциях значение переменной может быть определено путем подстановки конкретного значения вместо переменной и вычисления результата. Например, значение выражения 2x при x=3 будет равно 2*3=6.

Значение функции может быть определено путем подстановки значения аргумента в функцию и вычисления результата. Например, значение квадратной функции f(x)=x^2 при x=2 будет равно f(2)=2^2=4.

В математике значение также может быть использовано для оценки или сравнения различных величин. Например, значение функции может быть использовано для определения экстремумов или точек пересечения графиков.

Значение в математике является основополагающим понятием, которое позволяет нам оперировать с числами, выражениями и функциями, и делать выводы на основе этих значений.

Польза в повседневной жизни

Понимание и умение работать с понятием «5 часть» в математике имеет практическую пользу в повседневной жизни. Это помогает нам разбираться с долями, процентами и другими аспектами, где необходимо разделить что-то на пять равных частей.

Например, при дележе счета в ресторане на пять человек, каждому будет приходиться платить одну пятую общей суммы. Также это помогает при расчете скидок или наценок в магазинах, когда цена снижается или увеличивается на 20%, что является пятой частью от общей стоимости товара.

Знание 5 части также полезно при решении задач, связанных с распределением ресурсов или времени. Например, если у вас есть 5 часов на выполнение задания, то каждый час будет составлять одну пятую от общего времени.

Все эти примеры показывают, что понимание и умение работать с 5 частью в математике помогают нам разбираться с различными аспектами нашей повседневной жизни, где необходимо делить что-то на пять равных частей.

Виды задач

В математике существует несколько видов задач, которые можно решать с использованием 5 части. Рассмотрим некоторые из них:

1. Задачи на нахождение неизвестного значения: это задачи, в которых известны значения четырех из пяти величин, а нужно найти пятую. Например, известны длина и ширина прямоугольника, а нужно найти его площадь.

2. Задачи на нахождение значения известной величины: в таких задачах известны значения четырех величин, а нужно найти значение пятой величины. Например, известны площадь и одна из сторон прямоугольника, а нужно найти вторую сторону.

3. Задачи на нахождение неизвестной величины через известные связи: в таких задачах известны значения нескольких величин и связи между ними, а нужно найти значение пятой величины. Например, известны масса тела и его ускорение, а нужно найти силу, действующую на тело.

4. Задачи на нахождение неизвестной величины через известные свойства: в таких задачах известны значения нескольких величин и их свойства, а нужно найти значение пятой величины. Например, известны объем и плотность вещества, а нужно найти его массу.

5. Задачи на нахождение неизвестной величины через известные формулы: в таких задачах известны значения нескольких величин и формулы, связывающие эти величины, а нужно найти значение пятой величины. Например, известны масса и скорость тела, а нужно найти его импульс.

При решении задач на 5 часть важно уметь анализировать данные, видеть связи между величинами и применять соответствующие формулы и свойства.

Применение в других областях

• Физика: пятая часть применяется при решении задач на скорость, расстояние и время, а также при анализе графиков и закономерностей.
• Экономика: понимание пятой части помогает в вычислении процентов, прибыли, убытков и других финансовых показателей.
• Статистика: использование пятой части позволяет проводить анализ данных, вычислять среднее значение, стандартное отклонение и другие статистические показатели.
• Инженерия: пятая часть применяется при проектировании, моделировании и расчетах различных систем и конструкций.

Это лишь некоторые области, в которых знание пятой части в математике может быть полезным. Она является универсальным инструментом, который помогает в решении задач и анализе данных в различных сферах деятельности.

Выводы

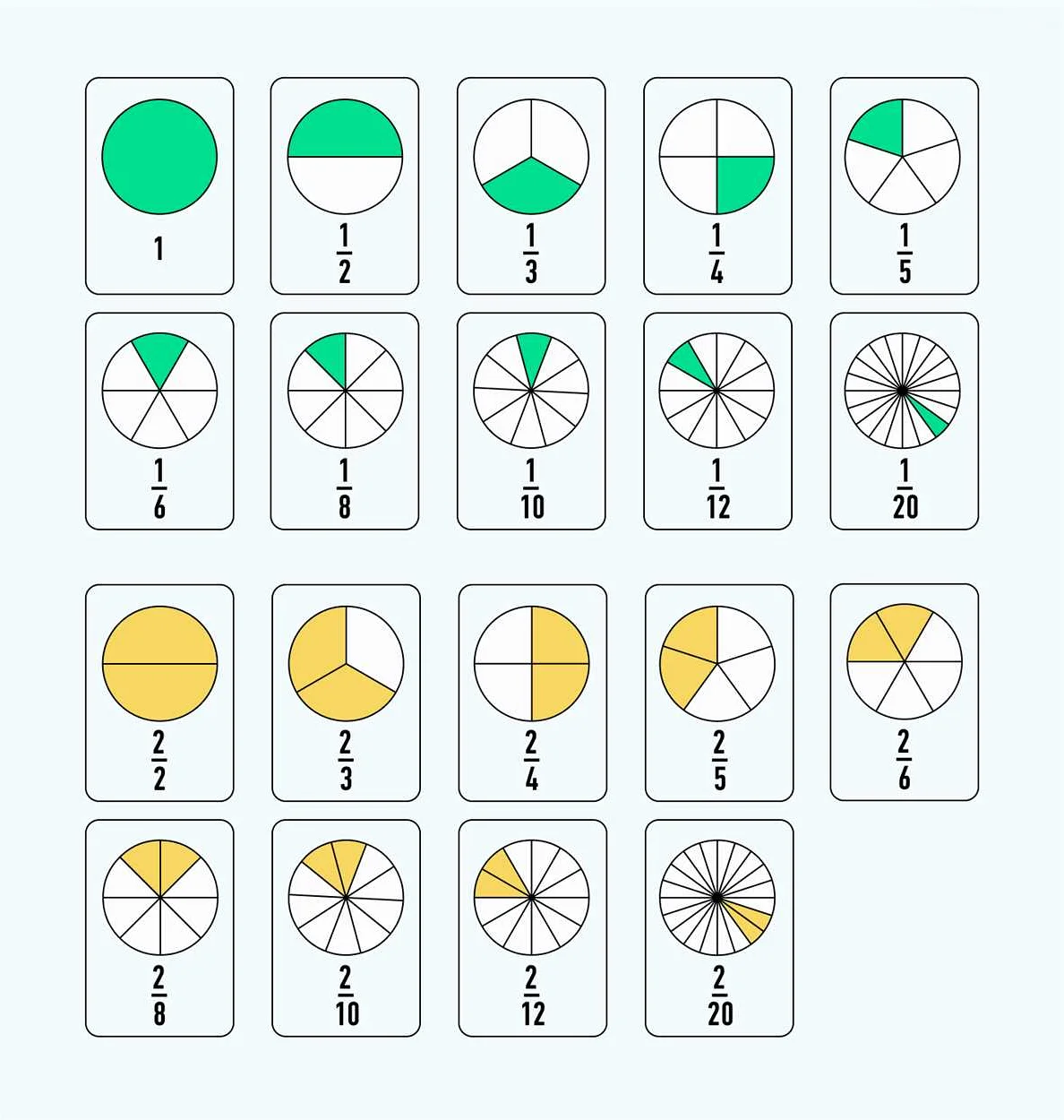
В пятой части математики мы рассмотрели различные понятия и методы, связанные с дробями, процентами и десятичными дробями. Мы изучили, как выполнять операции с этими числами, такие как сложение, вычитание, умножение и деление. Также мы разобрались с понятием пропорции и научились решать задачи, связанные с пропорциональными отношениями.

Дроби, проценты и десятичные дроби широко применяются в реальной жизни, и понимание этих понятий позволяет нам решать множество задач из разных областей. Применение математических методов и концепций помогает нам анализировать информацию, принимать решения и решать сложные задачи в повседневной жизни.

Важно понимать, что математика – это не просто набор формул и правил, но и инструмент для решения реальных проблем. Пятая часть математики помогает развить навыки логического мышления, анализа данных и применения математических концепций в реальных ситуациях.

Изучение пятой части математики предоставляет нам необходимые знания и навыки для более глубокого понимания мира и его функционирования. В дальнейшем это будет полезно для нашего образования, карьеры и общественной жизни.

Итак, пятая часть математики – это важный этап в изучении данной науки и является фундаментом для дальнейшего развития математических навыков и понимания мира в целом.

Видео по теме:

Что такое 5 часть в математике?

Пятая часть в математике — это одна из равных частей, на которые можно разделить целое число или объект. Если число или объект разделено на пять равных частей, каждая из них будет составлять пятую часть.

Как можно представить 5 часть в математике?

Пятая часть в математике может быть представлена в виде десятичной дроби, где числитель равен 1, а знаменатель равен 5 (1/5). Также ее можно представить в виде процента — 20%. Например, если у нас есть 20 яблок, то 5 частей будет равно 4 яблокам.

Как рассчитать 5 часть числа?

Для расчета пятой части числа, нужно число разделить на 5. Например, если у нас есть число 25, то пятая часть будет равна 25/5 = 5. То есть, пятая часть числа 25 равна 5.