Что такое делитель в математике
Содержимое
- 1 Что такое делитель в математике
Делитель в математике — это число, которое без остатка делится на другое число. Узнайте, как находить делители числа и как использовать их в различных задачах.
В математике делитель — это число, на которое данное число делится без остатка. Другими словами, делитель является множителем, который при умножении на другое число дает исходное число.
Делители играют важную роль в различных областях математики, включая арифметику, алгебру и теорию чисел. Они позволяют анализировать и классифицировать числа, а также решать различные задачи, связанные с делимостью.
Свойства делителей также имеют большое значение при работе с числами. Например, любое число делится на 1 и на само себя, поэтому эти числа являются делителями любого числа. Более того, делители могут быть положительными и отрицательными, и могут быть как простыми (т.е. не имеющими делителей, кроме 1 и самого себя), так и составными (т.е. имеющими делители, отличные от 1 и самого себя).
Например, для числа 12 делителями являются числа 1, 2, 3, 4, 6 и 12. Делители числа 12 образуют его набор делителей.
Знание того, что такое делитель, и понимание свойств делителей помогает в решении различных задач, связанных с числами и их свойствами. Изучение делителей также является важной частью математического образования и может быть полезно в повседневной жизни, например, при расчете долей или при факторизации чисел.
Что такое делитель в математике?
Делители являются одним из основных понятий в математике и широко используются в различных областях. Они помогают анализировать и работать с числами, а также находить различные свойства и закономерности.
У каждого числа есть минимальный делитель — число 1, и максимальный делитель — само число. Кроме того, каждое число имеет еще множество делителей, которые располагаются между минимальным и максимальным делителями.
Делители можно выразить в виде таблицы, где в первом столбце указываются все числа, а во втором столбце — их делители. Например, для числа 10 таблица делителей будет выглядеть следующим образом:
| 10 | 1, 2, 5, 10 |
Таким образом, делители — это числа, на которые данное число можно разделить без остатка. Они являются важным понятием в математике и используются для анализа чисел и нахождения различных свойств и закономерностей.
Видео по теме:
Определение делителя
Делители могут быть положительными и отрицательными. Например, для числа 12 положительными делителями являются 1, 2, 3, 4, 6 и 12, а отрицательными — -1, -2, -3, -4, -6 и -12.
Единица и само число также являются делителями для любого числа.
Число, которое делится на другое число, называется делимым, а результат деления — частным.
Например, число 15 делится без остатка на 3, поэтому 3 является его делителем.
Делители имеют важное значение в различных областях математики, таких как алгебра, арифметика и теория чисел. Они помогают нам анализировать и понимать свойства чисел и выполнять различные операции с ними.
Свойства делителя
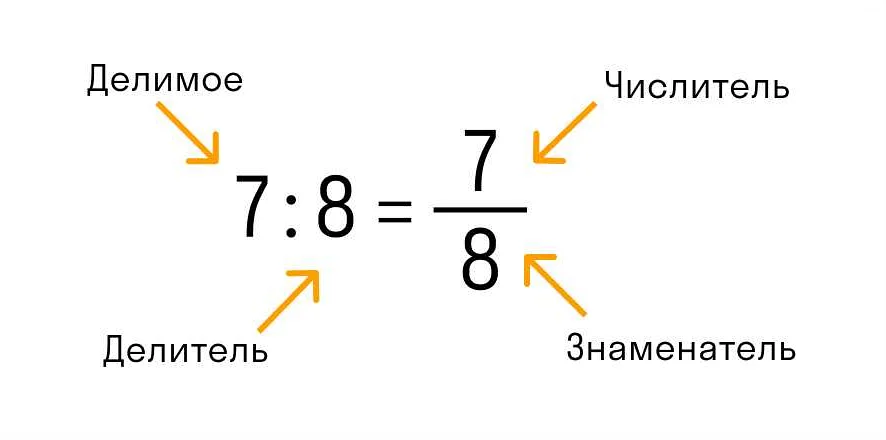
- Делитель всегда является меньшим или равным самому числу.
- Делитель всегда является положительным числом.
- Единица и само число всегда являются делителями числа.
- Если число делится на делитель без остатка, то оно также делится на любой делитель этого делителя.
- Если число делится на делитель без остатка, то оно также делится на любой множитель этого делителя.
- Два разных делителя числа не могут быть между собой взаимно простыми.
- Сумма всех делителей числа, включая единицу и само число, равна этому числу.
- Количество делителей числа можно найти с помощью факторизации числа.
- Наибольший общий делитель двух чисел является наибольшим делителем каждого из чисел.
Знание и применение свойств делителя позволяет решать различные математические задачи и находить особые числовые соотношения.
Вопрос-ответ:
Что такое делитель в математике?
В математике делитель — это число, на которое данное число делится нацело, то есть без остатка. Например, делителями числа 12 являются 1, 2, 3, 4, 6 и 12.
Как можно определить делитель числа?
Чтобы определить делитель числа, нужно проверить, делится ли это число на данное число без остатка. Если делится, то данное число является делителем. Например, чтобы определить, является ли число 3 делителем числа 15, нужно проверить, делится ли 15 на 3 без остатка.
Какие свойства имеют делители?
Делители числа обладают следующими свойствами: 1) Любое число является делителем самого себя и единицы. 2) Если число a является делителем числа b, а число b является делителем числа c, то число a также является делителем числа c. 3) Если число a является делителем числа b, а число b является делителем числа a, то числа a и b называются взаимно простыми.
Можно ли найти общие делители у двух чисел?
Да, можно найти общие делители у двух чисел. Общие делители — это числа, которые являются делителями обоих чисел. Например, общими делителями чисел 12 и 18 являются числа 1, 2, 3 и 6.
Какие примеры можно привести для понимания делителей?
Примеры делителей: для числа 10 делителями являются 1, 2, 5 и 10; для числа 8 — 1, 2, 4 и 8; для числа 15 — 1, 3, 5 и 15.
Примеры делителей

Рассмотрим некоторые примеры делителей:
- Делители числа 12: 1, 2, 3, 4, 6, 12.
- Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.
- Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
- Делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
- Делители числа 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Таким образом, делители числа могут быть как простыми числами, так и составными числами.
Чётные и нечётные делители

Делители числа делят его нацело без остатка. В математике выделяют два вида делителей: чётные и нечётные.
Чётные делители числа делятся на два без остатка, то есть являются чётными числами. Например, для числа 10 чётные делители будут 2, 4 и 10.
Нечётные делители числа не делятся на два без остатка, то есть являются нечётными числами. Например, для числа 15 нечётные делители будут 3 и 15.
Число 1 является особенным, так как оно имеет только один делитель — само себя. При этом 1 не является ни чётным, ни нечётным числом.
Знание о чётных и нечётных делителях числа помогает в решении различных задач, связанных с делимостью и делителями.
Ноль как делитель
Если мы попытаемся разделить число на ноль, то получим неопределенность и результат будет бесконечностью или неопределенным числом.
Ноль также не является делителем в определении простого числа. Простым числом называется число, которое делится нацело только на 1 и на само себя, и таким образом, число 0 не может быть простым числом.
Однако, в некоторых математических контекстах, ноль может играть особую роль. Например, в некоторых алгебраических системах, ноль может быть «делителем» других чисел, так как умножение на ноль приводит к получению нуля.
Таким образом, хотя ноль не является обычным делителем, он имеет свою специфическую роль и свойства в математике.
Делители простых чисел
Делители простых чисел можно найти, разделяя число на все возможные целые числа и проверяя, делится ли оно на эти числа без остатка.
Например, число 5 является простым числом, поскольку оно имеет только два делителя: 1 и 5. Аналогично, число 7 также является простым числом, поскольку его единственными делителями являются 1 и 7.
Простые числа играют важную роль в различных областях математики, таких как криптография, теория чисел и алгоритмы. Они также широко используются в науке и технике для решения различных задач.
Делители составных чисел
Простые делители составного числа являются простыми числами, которые делят это число без остатка. Например, число 12 имеет простые делители: 2, 3 и 6.
Составные делители составного числа являются составными числами, которые делят это число без остатка. Например, число 15 имеет составные делители: 3 и 5.
Делители составных чисел можно найти путем разложения числа на простые множители и нахождения всех возможных комбинаций этих множителей.
Например, число 24 можно разложить на простые множители: 2 * 2 * 2 * 3. Таким образом, делители числа 24: 1, 2, 3, 4, 6, 8, 12 и 24.
Зная делители составного числа, можно проводить различные математические операции, такие как нахождение наибольшего общего делителя или наименьшего общего кратного.
Делители и наименьшее общее кратное
Наименьшее общее кратное (НОК) двух чисел — это наименьшее положительное число, которое делится на оба числа без остатка. Для нахождения НОК двух чисел нужно найти их общие делители и умножить их наибольшие степени. Например, для чисел 4 и 6, их общими делителями являются 1, 2 и 3. Наибольшая степень 2 равна 2, а наибольшая степень 3 равна 1. Умножив эти степени на соответствующие делители, получим НОК, равное 2 * 3 = 6.
Наименьшее общее кратное также можно найти с помощью таблицы делителей. Для этого необходимо составить таблицу с делителями каждого числа и выписать все простые делители только один раз, а затем умножить их наибольшие степени.
ЧислоДелители
| 4 | 1, 2, 4 |
| 6 | 1, 2, 3, 6 |
Из таблицы видно, что наибольшая степень делителя 2 равна 2, а наибольшая степень делителя 3 равна 1. Умножив эти степени на соответствующие делители, получим НОК, равное 2 * 3 = 6.
Таким образом, делители и наименьшее общее кратное являются важными понятиями в математике, которые используются для решения различных задач и построения математических моделей.
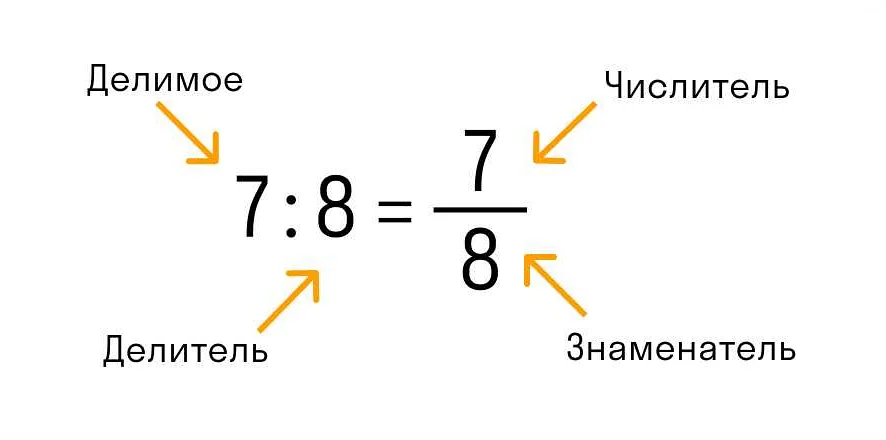



Очень понятная и информативная статья! Я всегда слышала о понятии «делитель» в математике, но никогда не понимала его полностью. Теперь у меня есть четкое представление об этом. Очень интересно узнать, что делитель — это число, которое делится на другое число без остатка. И то, что каждое число имеет свои делители, в том числе и единицу и само себя. Интересно было узнать о свойствах делителей, например, о том, что они упорядочивают числа по возрастанию. Приведенные примеры также помогли мне лучше понять это понятие. Теперь я чувствую себя более уверенной в знании математики! Спасибо за статью!