Составное число что это такое в математике

Составное число в математике — это натуральное число, которое имеет более двух делителей. В статье рассматривается определение составных чисел, их свойства и примеры. Узнайте, как определить, является ли число составным и почему они играют важную роль в теории чисел.

Составным числом в математике называется натуральное число, которое имеет больше двух делителей. Другими словами, это число, которое можно разложить на два или более простых множителей. Например, число 12 является составным, так как его можно разложить на множители 2 и 6.

Основное свойство составных чисел заключается в том, что они имеют делители, отличные от 1 и самого числа. Иными словами, для любого составного числа существует такое число, на которое оно делится без остатка. Например, для числа 8 делителями будут числа 2 и 4.

Существует бесконечное множество составных чисел. Например, если умножить любое простое число на другое простое число, получится составное число. Кроме того, можно взять любое составное число и добавить к нему константу, чтобы получить еще одно составное число. Например, числа 15 и 17 оба являются составными, и их сумма 32 также будет составным числом.

Итак, составное число – это число, которое имеет больше двух делителей и которое можно разложить на два или более простых множителей. Составные числа обладают свойством иметь делители, отличные от 1 и самого числа. Они составляют бесконечное множество и могут быть получены путем умножения простых чисел или добавления константы к другому составному числу.

Составное число в математике: основное понятие

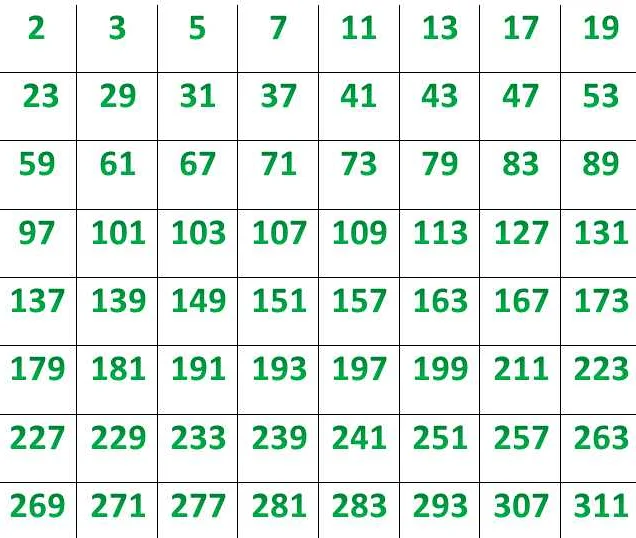
Примерами составных чисел являются 4, 6, 8, 9, 10 и так далее. Чтобы определить, является ли число составным, необходимо найти все его делители и проверить, есть ли среди них числа, отличные от единицы и самого числа. Если такие числа есть, то число является составным, в противном случае оно является простым.

Составные числа имеют свойства, которые отличают их от простых чисел. Например, составное число всегда можно представить в виде произведения простых множителей. Это называется разложением на множители. Также составные числа обладают свойством того, что у них всегда есть несколько делителей, в то время как у простых чисел делителей только два – единица и само число.

Примеры составных чиселРазложение на множители

4	2 × 2
6	2 × 3
8	2 × 2 × 2
9	3 × 3
10	2 × 5

Составное число: определение и примеры

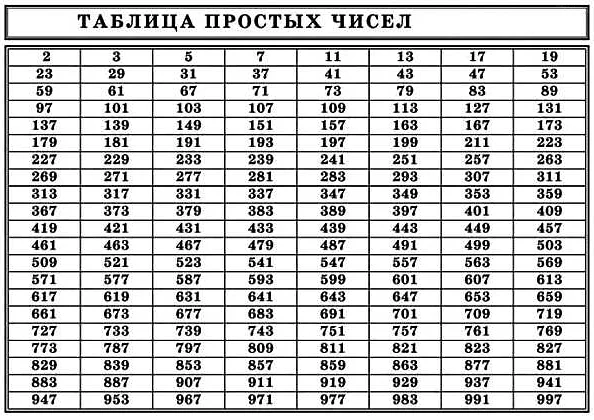
Например, число 6 является составным числом, так как оно имеет делители 1, 2, 3 и 6. Оно может быть разложено на множители 2 и 3.

Другим примером составного числа является число 15. Оно имеет делители 1, 3, 5 и 15, и может быть разложено на множители 3 и 5.

Составное числоРазложение на множители

6	2 × 3
15	3 × 5
21	3 × 7

Составные числа играют важную роль в различных областях математики, включая теорию чисел и криптографию. Изучение свойств составных чисел позволяет лучше понять их структуру и использовать их в различных алгоритмах и задачах.

Как определить, является ли число составным?

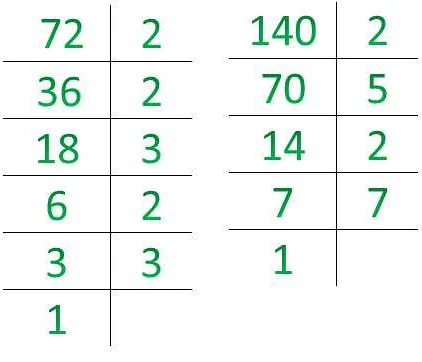
Разложение на простые множители происходит путем деления числа на все возможные простые числа, начиная с 2 и двигаясь дальше по возрастанию. Если число делится без остатка, то оно является составным, иначе – продолжаем делить на следующее простое число. Если в результате деления получается остаток, значит число является простым.

Пример:

ЧислоРазложение на простые множители

12	2 * 2 * 3
17	простое число
30	2 * 3 * 5

Таким образом, число 12 является составным, так как его разложение содержит более двух множителей (2, 2 и 3), число 17 является простым, так как оно не делится ни на одно другое число кроме себя самого и единицы, а число 30 также является составным, так как его разложение содержит более двух множителей (2, 3 и 5).

Составные числа: основные свойства

Основные свойства составных чисел:

1. Разложение на простые множители: Любое составное число можно разложить на простые множители. Это позволяет нам представить число в виде произведения его простых делителей.

2. Бесконечность составных чисел: Составных чисел бесконечно много. Это следует из того, что простых чисел, которые являются основными строительными блоками составных чисел, также бесконечно много.

3. Делители составного числа: Составное число имеет более двух делителей. Это означает, что оно делится не только на 1 и само число, но также на другие числа.

4. Простые числа как делители: Составное число может иметь простые числа в качестве своих делителей. Это позволяет нам проверить, является ли число составным, разлагая его на простые множители и проверяя, есть ли в полученном разложении простые числа.

5. Факторизация составных чисел: Факторизация составных чисел – это процесс разложения составного числа на простые множители. Факторизация помогает нам понять структуру числа и выявить его делители.

Изучение составных чисел и их свойств играет важную роль в математике. Они являются основой для понимания многих других понятий и теорем, таких как нахождение наибольшего общего делителя и нахождение наименьшего общего кратного.

Разложение на простые множители

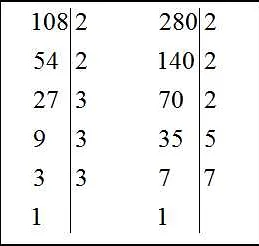
Для разложения числа на простые множители следует последовательно делим его на наименьшие простые числа, начиная с 2. Если число делится на это простое число без остатка, оно записывается в виде произведения этого простого числа и оставшегося частного. Если число не делится на это простое число, переходим к следующему простому числу.

Процесс разложения продолжается до тех пор, пока оставшееся число не станет простым. В результате получается разложение исходного числа на простые множители в виде произведения всех простых множителей.

Исходное числоПростые множители

12	2 × 2 × 3
24	2 × 2 × 2 × 3
36	2 × 2 × 3 × 3

Разложение на простые множители позволяет легко определить все делители числа, вычислить наибольший общий делитель двух чисел и наименьшее общее кратное. Также разложение на простые множители используется в теории чисел и алгебре для решения различных задач и доказательств.

Свойство делимости составного числа

Существуют два типа делителей для составных чисел: простые и составные. Простые делители – это числа, которые делят составное число без остатка и имеют только два делителя: 1 и само число. Например, числа 2, 3, 5 и 7 являются простыми делителями числа 30.

Составные делители – это числа, которые также делят составное число без остатка, но имеют более двух делителей. Например, для числа 30 составные делители это числа 6, 10 и 15, так как они делятся на 1, сами себя и другие числа.

Свойство делимости составного числа позволяет найти все его делители и разложить его на простые множители. Это основной шаг при решении задач, связанных с составными числами, таких как нахождение наибольшего общего делителя или наименьшего общего кратного.

Сумма делителей составного числа

Сумма делителей составного числа – это сумма всех чисел, на которое заданное составное число делится без остатка. Для вычисления суммы делителей составного числа необходимо найти все его делители и проссумировать их.

Для примера, рассмотрим составное число 12. Его делители: 1, 2, 3, 4, 6, 12. Сумма этих делителей будет равна 28.

Сумма делителей составного числа может быть использована для решения различных задач. Например, сумма делителей составного числа может помочь определить, является ли число совершенным, изобильным или недостаточным.

Если сумма делителей составного числа больше самого числа, то такое число называется изобильным. Если сумма делителей составного числа меньше самого числа, то такое число называется недостаточным. Если сумма делителей составного числа равна самому числу, то такое число называется совершенным.

Например, число 12 является изобильным числом, так как сумма его делителей (1 + 2 + 3 + 4 + 6) равна 16, что больше самого числа (12).

Примеры использования составных чисел

Составные числа играют важную роль в математике и имеют широкий спектр применений. Ниже приведены несколько примеров использования составных чисел:

1. Факторизация чисел: составные числа используются при разложении числа на простые множители. Это позволяет нам легко находить общие множители, находить наименьшее общее кратное и решать задачи, связанные с делимостью.
2. Криптография: составные числа используются в различных алгоритмах шифрования, таких как RSA. Они играют важную роль в обеспечении безопасности при передаче информации.
3. Тесты простоты чисел: составные числа используются в различных тестах простоты, таких как тест Ферма и тест Миллера-Рабина. Эти тесты позволяют нам определить, является ли число простым или составным.
4. Математические моделирование: составные числа используются для построения различных математических моделей, таких как модели роста населения и экономические модели. Они помогают нам понять и предсказывать различные явления и процессы в природе и обществе.

Это лишь некоторые примеры использования составных чисел. Они широко применяются в различных областях математики, науки и техники, и их значимость трудно переоценить.

Алгоритмы нахождения составных чисел

Существует несколько алгоритмов, которые позволяют эффективно находить составные числа.

1. Метод факторизации: Этот метод основан на разложении числа на простые множители. При использовании этого метода, число проверяется на делимость на все числа от 2 до корня квадратного из числа. Если число делится на одно из этих чисел, оно считается составным. Если число не делится ни на одно из этих чисел, оно считается простым.
2. Метод перебора: Этот метод заключается в переборе всех возможных делителей числа. Если число делится без остатка на какое-либо из этих чисел, оно считается составным. Если число не делится ни на одно из этих чисел, оно считается простым. Этот метод является наиболее простым, но при больших числах может быть неэффективным.
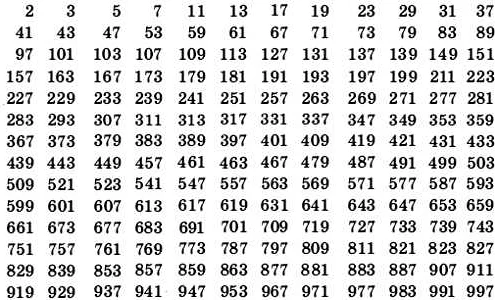
3. Метод решета Эратосфена: Этот метод основан на исключении всех чисел, которые являются кратными простым числам. Сначала создается список всех чисел от 2 до заданного числа. Затем поочередно исключаются все числа, кратные каждому из простых чисел. Оставшиеся числа считаются составными.

Выбор конкретного алгоритма зависит от требуемой эффективности и точности нахождения составных чисел.

Вопрос-ответ:

Что такое составное число?

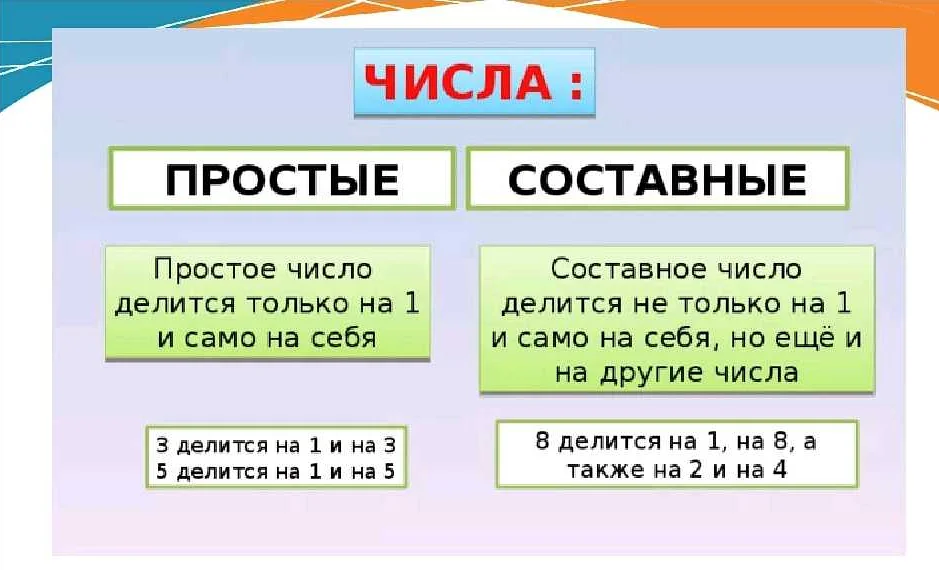
Составное число — это натуральное число, большее единицы, которое имеет более двух делителей. Иными словами, это число, которое можно разложить на простые множители.

Какие свойства имеют составные числа?

У составных чисел есть несколько интересных свойств. Во-первых, каждое составное число можно представить в виде произведения простых множителей. Во-вторых, у составного числа всегда есть делители, кроме единицы и самого числа. Наконец, составные числа можно разложить на простые множители единственным образом.

Как найти все делители составного числа?

Для нахождения всех делителей составного числа можно последовательно делить его на все натуральные числа от 1 до самого числа. Если деление происходит без остатка, то это число является делителем.

Как определить, является ли число составным?

Для определения, является ли число составным, нужно проверить, есть ли у него делители, кроме 1 и самого числа. Для этого можно последовательно делить число на все натуральные числа от 2 до квадратного корня из числа. Если деление происходит без остатка, то число является составным.

Видео по теме: