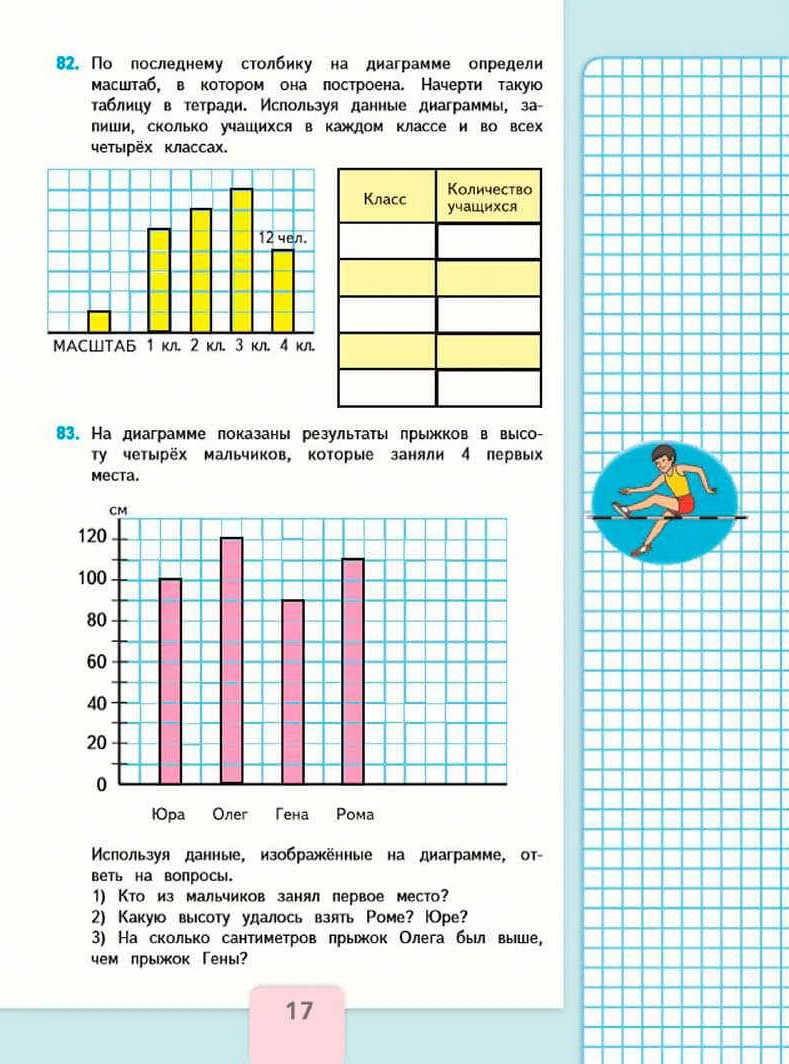
Что такое диаграмма в математике 5 класс

В данной статье рассказывается о том, что представляет собой диаграмма в математике для учеников 5 класса. Описываются основные типы диаграмм, их назначение и применение в решении задач. Также приводятся примеры и объяснения для лучшего понимания материала.

В математике 5 класса диаграмма — это графическое представление информации, которое помогает наглядно и легко понять различные зависимости и сравнения. Диаграммы широко используются для анализа данных и решения задач в различных областях жизни.

Основное понятие, связанное с диаграммами, — это переменная. Переменная это величина, которая может принимать различные значения. Например, переменная может быть числом, цветом, размером и т.д. Переменные используются для представления данных на диаграммах.

Существует несколько типов диаграмм, которые учат в 5 классе. Одним из самых простых типов диаграмм является круговая диаграмма. В круговой диаграмме данные представляются в виде секторов, пропорциональных исходным значениям. Это позволяет проиллюстрировать относительные доли и сравнить различные категории между собой.

Еще одним типом диаграммы является столбчатая диаграмма. В столбчатой диаграмме данные представлены в виде столбцов, пропорциональных исходным значениям. Столбцы могут быть вертикальными или горизонтальными, в зависимости от ориентации диаграммы. Столбчатая диаграмма позволяет наглядно сравнивать значения в разных категориях.

Другие типы диаграмм, которые изучают в 5 классе, включают линейные диаграммы, круговые диаграммы и точечные диаграммы. Каждый тип диаграммы имеет свои особенности и применение в разных ситуациях. Понимание основных понятий и типов диаграмм поможет ученикам использовать их в своей работе и анализе данных.

Диаграмма в математике 5 класс

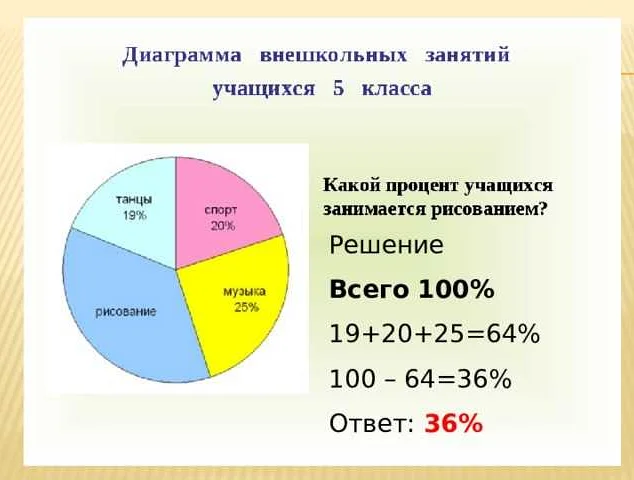
Основными понятиями, связанными с диаграммами, являются:

1. График — это вид диаграммы, который отражает зависимость одной величины от другой. Графики могут быть линейными, столбчатыми, круговыми и так далее.

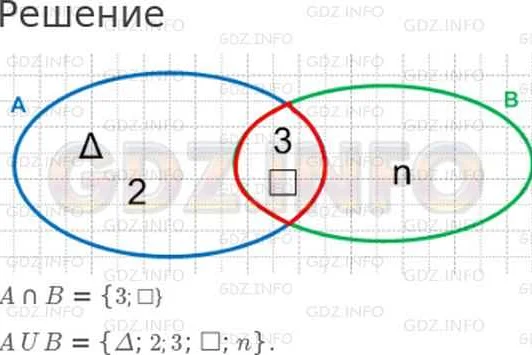
2. Диаграмма Венна — это диаграмма, которая представляет собой объединение или пересечение множеств. Диаграмма Венна позволяет наглядно показать, какие элементы входят в каждое множество и какие элементы являются общими.

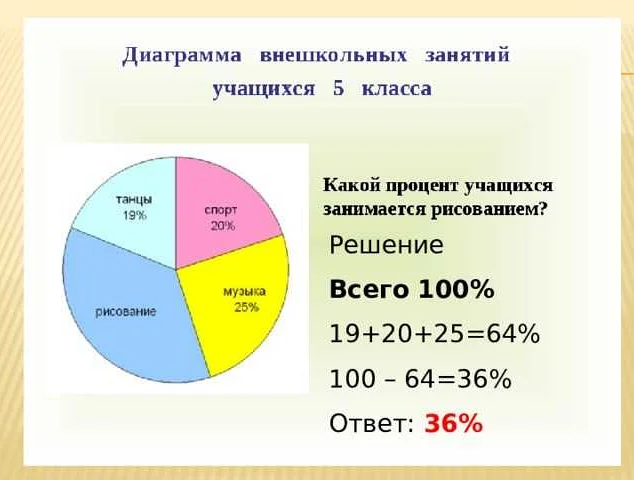
3. Круговая диаграмма — это диаграмма, которая представляет собой круг, разделенный на секторы, каждый из которых соответствует определенной величине или категории. Круговая диаграмма позволяет наглядно показать долю каждой величины в общем объеме.

4. Столбчатая диаграмма — это диаграмма, которая представляет собой набор столбиков разной высоты, каждый из которых соответствует определенной величине или категории. Столбчатая диаграмма позволяет сравнить различные значения и выделить наибольшие и наименьшие.

Использование диаграмм в математике 5 класса позволяет ученикам лучше понять и запомнить математические понятия, развивает навыки анализа и логического мышления, а также помогает визуально представить информацию и делать выводы на основе полученных данных.

Видео по теме:

Определение и основные понятия

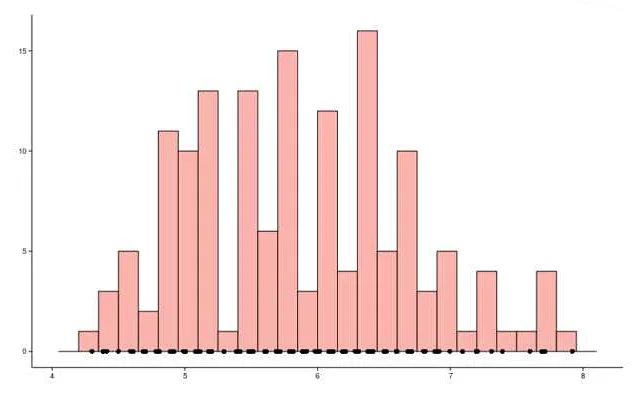
Основные понятия, связанные с диаграммами, включают:

• Переменные: это характеристики или свойства, которые измеряются или наблюдаются и представляются на диаграмме. Например, в диаграмме о количестве проданных билетов на концерт, переменная может быть «количество билетов».
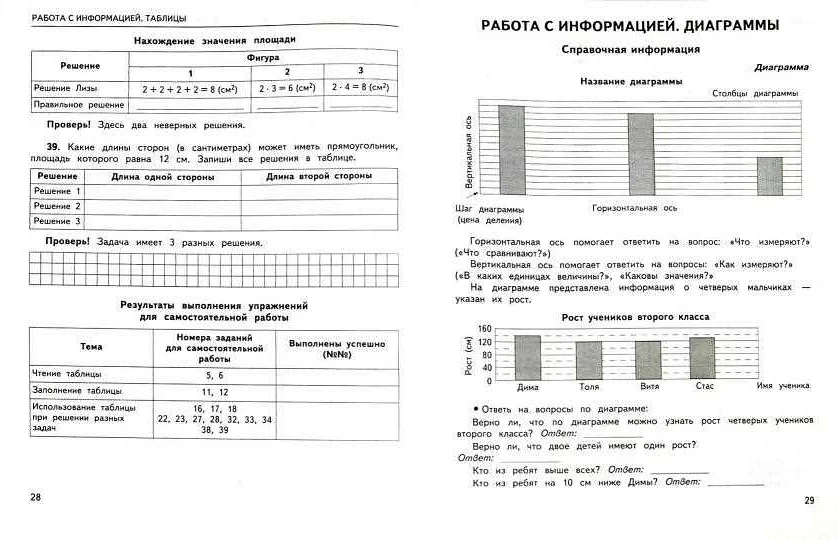
• Оси: это линии или полосы, на которых отображаются значения переменных. Оси могут быть вертикальными (ось y) или горизонтальными (ось x).
• Значения: это числа или категории, которые представляют конкретные значения переменных и отображаются на осях. Например, на оси x могут быть представлены значения «январь», «февраль», «март» и т.д.
• Масштаб: это отношение между значениями на осях и реальными значениями переменных. Масштаб позволяет установить соотношение между отображаемыми данными и их фактическими значениями.
• Заголовок: это текстовая надпись, которая описывает содержимое диаграммы и помогает понять ее цель или тему.
• Легенда: это обозначения или цветовые коды, которые объясняют значения или категории, представленные на диаграмме. Легенда помогает разобраться в значении каждого элемента диаграммы.

Понимание этих основных понятий помогает увидеть структуру и значение диаграммы, а также сделать правильные выводы и анализ данных, представленных на ней.

Типы диаграмм в математике

В математике существует несколько основных типов диаграмм, которые помогают визуализировать различные понятия и закономерности.

Круговая диаграмма – это диаграмма, которая представляет собой круг, разделенный на несколько секторов. Каждый сектор соответствует определенной категории или элементу, а его площадь пропорциональна значению этой категории в общем объеме.

Столбчатая диаграмма – это диаграмма, которая представляет собой систему столбцов, расположенных на горизонтальной или вертикальной оси. Высота каждого столбца соответствует значению определенной категории или элемента, а ширина столбцов может быть одинаковой или различной.

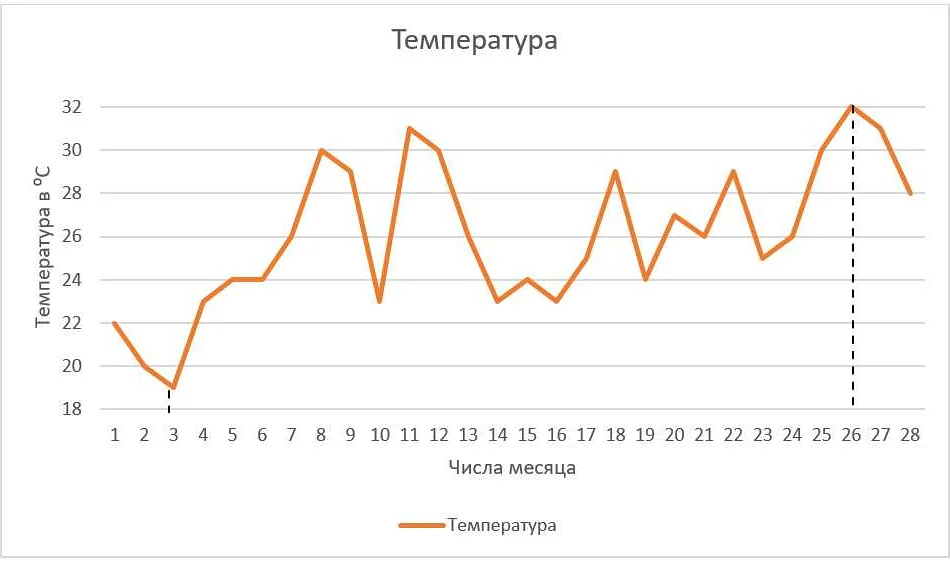
Линейная диаграмма – это диаграмма, которая представляет собой график, в котором значения различных элементов отображаются в виде точек, соединенных линиями. Линейная диаграмма позволяет наглядно показать изменение величин с течением времени или другого параметра.

Гистограмма – это диаграмма, которая представляет собой систему прямоугольников, расположенных на горизонтальной или вертикальной оси. Высота каждого прямоугольника соответствует значению определенной категории или элемента, а ширина прямоугольников может быть одинаковой или различной.

Точечная диаграмма – это диаграмма, которая представляет собой график, в котором значения различных элементов отображаются в виде точек на плоскости. Точечная диаграмма позволяет наглядно показать распределение значений и выявить возможные связи между ними.

Использование различных типов диаграмм в математике помогает более наглядно представить данные, анализировать их и делать выводы на основе полученной информации.

Вопрос-ответ:

Какие основные понятия и типы диаграмм существуют в математике для 5 класса?

В математике для 5 класса существуют различные типы диаграмм, такие как круговая диаграмма, столбчатая диаграмма и линейная диаграмма. Основные понятия, связанные с диаграммами, включают данные, переменные, оси, масштаб и легенду.

Какие данные можно представить с помощью круговой диаграммы?

Круговая диаграмма используется для представления данных, которые образуют часть целого. Например, можно представить процентное соотношение результата голосования, распределение расходов по категориям или долю населения разных стран.

Как строится столбчатая диаграмма и для чего она используется?

Столбчатая диаграмма представляет собой набор вертикальных столбиков, где высота каждого столбика соответствует значению переменной. Она используется для сравнения количественных данных или категорий. Например, можно отобразить количество проданных товаров по дням недели или сравнить рост разных растений.

Как использовать линейную диаграмму для представления данных?

Линейная диаграмма представляет собой набор точек, соединенных линией, где каждая точка отображает значение переменной в определенный момент времени или на определенной позиции. Она используется для отображения изменений величины во времени. Например, можно отобразить изменение температуры в течение дня или показать рост населения города за несколько лет.

Какие элементы включает в себя диаграмма?

Диаграмма включает в себя несколько элементов, включая данные, переменные, оси, масштаб и легенду. Данные — это числа или категории, которые нужно представить. Переменные — это факторы, которые влияют на данные. Оси — это линии, которые помогают ориентироваться на диаграмме. Масштаб — это единицы измерения на осях, которые позволяют сравнивать данные. Легенда — это объяснение символов или цветов, используемых на диаграмме.

Столбчатая диаграмма

Для построения столбчатой диаграммы необходимо выполнить следующие шаги:

1. Выбрать ось X и ось Y. Ось X обычно используется для обозначения категорий, а ось Y – для числовых значений.
2. Отметить на оси X категории, которые будут представлены на диаграмме.
3. Отметить на оси Y значения, которые будут соответствовать каждой категории.
4. Построить прямоугольные столбцы, которые будут представлять каждую категорию. Высота столбцов соответствует значениям на оси Y.
5. Подписать оси и столбцы, добавить заголовок диаграммы для лучшего понимания данных.

Столбчатые диаграммы широко используются в различных областях, таких как статистика, экономика, бизнес-анализ и другие. Они помогают наглядно представить большие объемы данных и выявить закономерности, тренды и различия между категориями.

Круговая диаграмма

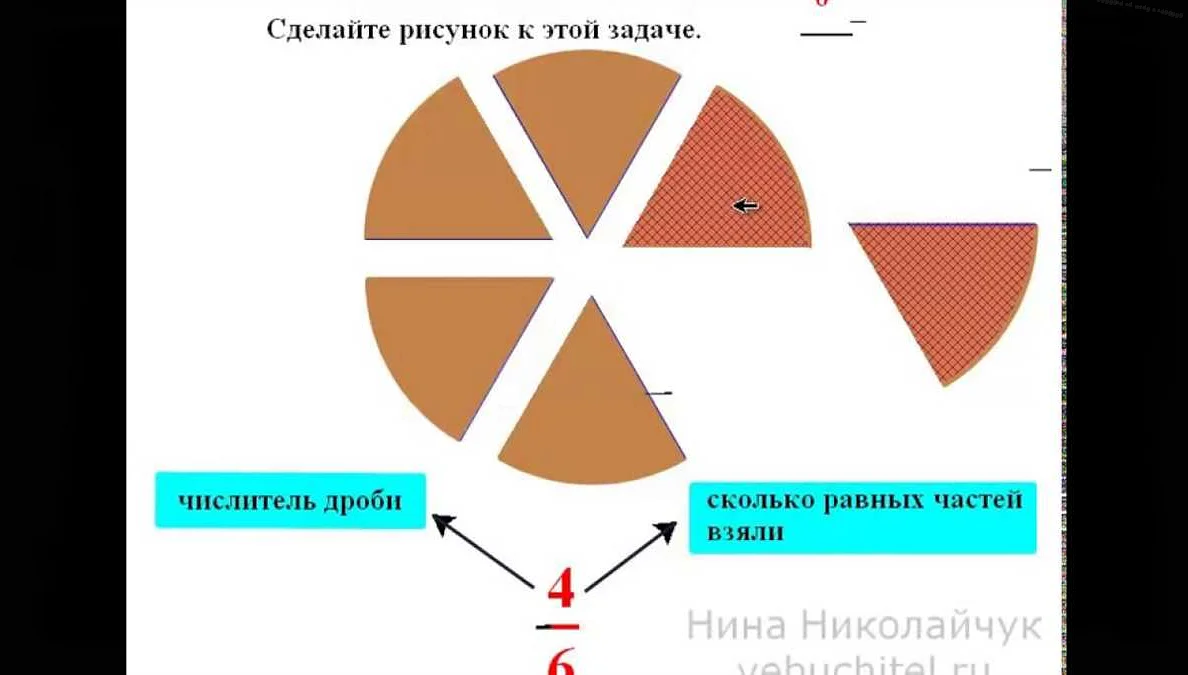
Круговые диаграммы часто используются для визуализации процентного соотношения частей целого. Они помогают наглядно показать, какую долю занимает каждая часть в общем объеме.

Для построения круговой диаграммы нужно знать процентное соотношение каждой категории. Часто эти данные представляются в виде таблицы, где одна колонка содержит названия категорий, а другая – процентные значения.

КатегорияПроцентное соотношение

Категория 1	30%
Категория 2	20%
Категория 3	15%
Категория 4	35%

На основе этих данных можно построить круговую диаграмму, где каждый сектор будет соответствовать определенной категории и его площадь будет пропорциональна процентному соотношению этой категории.

Круговые диаграммы обладают высокой информативностью и позволяют быстро воспринять соотношение между различными категориями. Они часто используются в статистике, экономике, бизнесе и других областях для наглядного представления данных и принятия важных решений.

Линейная диаграмма

Основная структура линейной диаграммы — горизонтальная ось X и вертикальная ось Y. По горизонтальной оси располагаются категории или переменные данных, а по вертикальной оси указываются их значения или количество. Затем, на диаграмме отмечаются точки или столбцы, соответствующие значениям данных. Соединение точек линией позволяет увидеть общую тенденцию изменения данных.

Линейная диаграмма широко используется в математике для анализа и визуализации временных рядов, тенденций, зависимостей и других видов данных. Она позволяет сравнивать значения разных переменных в разные моменты времени, а также выявлять закономерности и тренды. Линейная диаграмма помогает структурировать и упорядочить данные, делает их более понятными и доступными для восприятия.

Преимущества использования линейной диаграммы:

• Простота восприятия
• Удобство сравнения значений
• Возможность анализа и выявления трендов
• Гибкость в отображении различных типов данных
• Удобство внесения изменений и обновления данных

Линейная диаграмма является мощным инструментом в анализе данных и принятии решений. Она помогает наглядно представить информацию, сделать выводы и увидеть закономерности, что является важным в учебных и практических целях.

Плоская и пространственная диаграмма

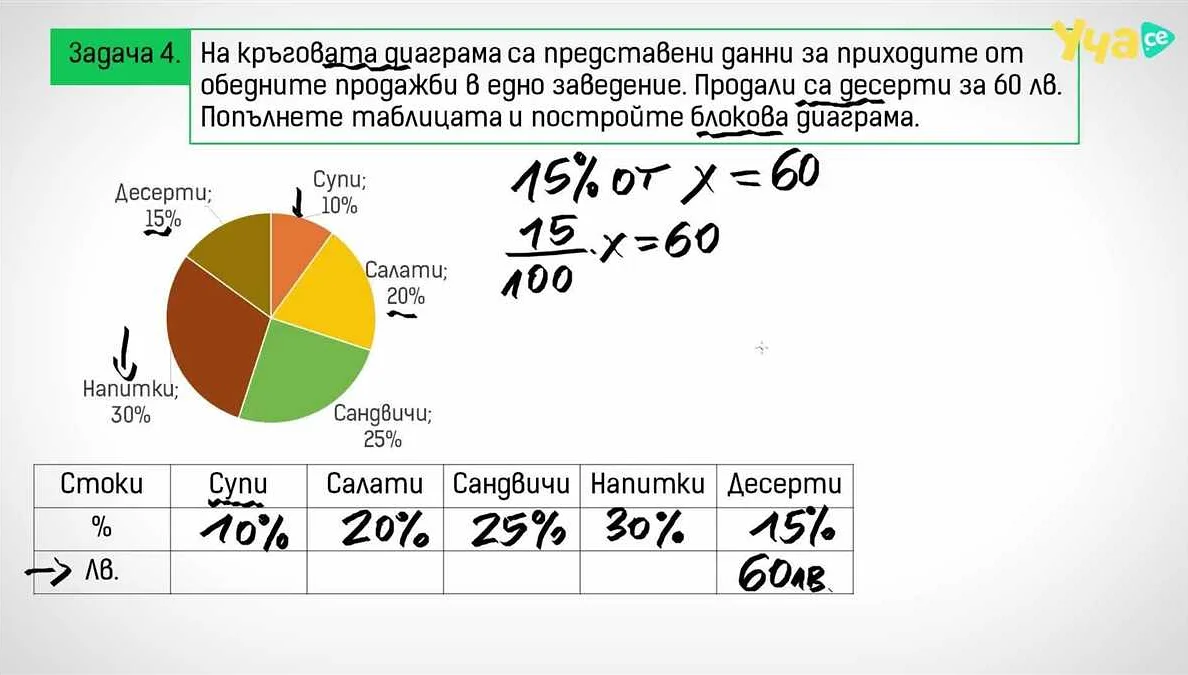
В математике существуют два основных типа диаграмм: плоская и пространственная. Оба типа диаграмм представляют собой графическое изображение данных и используются для визуализации информации.

Плоская диаграмма – это диаграмма, которая представляет данные на плоскости. Она имеет две оси – горизонтальную (ось абсцисс) и вертикальную (ось ординат), на которых откладываются значения различных характеристик или переменных. Плоская диаграмма может быть различных типов, таких как столбчатая, круговая, точечная и линейная диаграммы.

Пространственная диаграмма – это диаграмма, которая представляет данные в трехмерном пространстве. Она имеет оси x, y и z, на которых откладываются значения переменных. Пространственная диаграмма используется для визуализации сложных данных, которые не могут быть полностью представлены на плоскости. Примером пространственной диаграммы может служить трехмерная столбчатая диаграмма, где на трех осях откладываются значения трех переменных.

Как плоские, так и пространственные диаграммы помогают наглядно представить информацию и упростить ее анализ. Они широко используются в различных областях, включая статистику, экономику, науку и бизнес.

Использование диаграмм в математических задачах

Диаграммы в математике могут быть очень полезными инструментами при решении задач. Они позволяют наглядно представить информацию и легче анализировать ее. Вот несколько способов использования диаграмм в математических задачах:

1. Диаграмма Венна

Диаграмма Венна – это графическое представление множеств и их взаимосвязей. Она состоит из нескольких пересекающихся кругов, каждый из которых представляет отдельное множество. Диаграмма Венна может быть использована для решения задач на пересечение и объединение множеств.

2. График

График – это графическое представление функции или зависимости между двумя переменными. Он позволяет визуально представить изменение значений и анализировать их. Графики могут быть использованы для решения задач на построение и анализ функций, а также для решения задач о движении и изменении величин.

3. Гистограмма

Гистограмма – это столбчатая диаграмма, которая позволяет представить частоту или относительную частоту различных значений или категорий. Гистограммы могут быть использованы для решения задач на анализ данных и статистику.

4. Круговая диаграмма

Круговая диаграмма – это графическое представление данных в виде круга, разделенного на секторы, пропорциональные величинам данных. Круговые диаграммы позволяют наглядно представить доли и соотношения различных категорий. Они могут быть использованы для решения задач на анализ долей и процентов.

5. Линейная диаграмма

Линейная диаграмма – это графическое представление данных в виде линии, отражающей зависимость между двумя переменными. Линейные диаграммы позволяют визуализировать тенденции и изменения величин. Они могут быть использованы для решения задач на анализ трендов и прогнозирование.

Использование диаграмм в математических задачах позволяет упростить анализ информации, наглядно представить связи и зависимости, а также делать выводы на основе графических представлений. При решении задач с использованием диаграмм важно уметь анализировать и интерпретировать полученные результаты.

Примеры задач с использованием диаграмм

Диаграммы могут быть очень полезными инструментами для решения математических задач. Рассмотрим несколько примеров задач, в которых можно использовать диаграммы.

Пример 1: В классе 25 учеников. 15 из них увлекаются футболом, 10 — хоккеем, 5 — теннисом. Сколько учеников увлекаются только футболом и теннисом?

Для решения этой задачи можно использовать диаграмму Эйлера. На диаграмме изобразим три круга, каждый из которых представляет учеников, увлекающихся футболом, хоккеем и теннисом. Пересечение кругов показывает, сколько учеников увлекаются несколькими видами спорта.

Пример 2: В магазине продаются книги, журналы и газеты. Книги стоят 150 рублей, журналы — 50 рублей, газеты — 20 рублей. Если покупатель купил 5 книг, 10 журналов и 15 газет, сколько денег он потратил?

Для решения этой задачи можно использовать столбчатую диаграмму. На диаграмме изобразим три столбца, каждый из которых представляет стоимость книг, журналов и газет. Высота каждого столбца будет соответствовать количеству купленных предметов, а площадь каждого столбца — суммарной стоимости этих предметов. После этого можно просто сложить стоимости каждого столбца, чтобы найти общую сумму, потраченную покупателем.

Пример 3: У Маши есть коробка с разными мячами: футбольным, баскетбольным, волейбольным и теннисным. Футбольные мячи занимают 1/2 коробки, баскетбольные — 1/4 коробки, волейбольные — 1/8 коробки, а теннисные — 1/8 коробки. Если всего в коробке 16 мячей, сколько в коробке футбольных мячей?

Для решения этой задачи можно использовать круговую диаграмму. На диаграмме изобразим круг, который представляет коробку с мячами. Разделим этот круг на части, пропорциональные долям, занимаемым каждым видом мячей. Тогда можно определить, какая доля круга соответствует футбольным мячам, и просто умножить ее на общее количество мячей, чтобы найти количество футбольных мячей в коробке.

Это только некоторые примеры задач, в которых можно использовать диаграммы. Диаграммы помогают наглядно представить информацию и решить задачу более эффективно. Рекомендуется использовать диаграммы при решении различных математических задач, особенно если в них присутствуют сравнения и отношения между числами и объектами.