Что такое диаграмма по математике 4 класс

Что такое диаграмма по математике 4 класс? Узнайте, как диаграмма может помочь ученикам 4 класса представить данные и сравнить их визуально. Узнайте, как использование диаграммы может помочь развить навыки анализа и интерпретации данных учеников 4 класса.

Диаграмма – это графическое представление информации, которое помогает наглядно отобразить данные и сравнить их величины. Она является одним из важных инструментов, используемых в математике. В четвертом классе ученики изучают основные понятия диаграмм и учатся строить и анализировать их.

Одним из основных понятий, которое необходимо знать при работе с диаграммами, является «величина». Величина представляет собой измеряемое свойство объекта или явления. Например, величинами могут быть рост детей, количество яблок в корзине или продолжительность дождя.

Для визуального представления величин на диаграмме используются различные геометрические фигуры, такие как столбцы, круги или секторы. Каждая фигура соответствует определенной величине и имеет свою высоту или угол. Таким образом, ученики могут сравнивать величины и делать выводы о их соотношении.

Например, если на диаграмме изображены столбцы разной высоты, то можно сравнить их и сказать, какая величина наибольшая, а какая наименьшая. Это поможет ученикам визуализировать информацию и легче усвоить математические понятия.

На уроках математики в четвертом классе ученики изучают различные виды диаграмм, такие как столбчатая диаграмма, круговая диаграмма и линейная диаграмма. Ученики также учатся строить диаграммы на основе предоставленных данных и анализировать полученные результаты. Работа с диаграммами помогает учащимся развивать навыки анализа и логического мышления, а также улучшает их визуальное восприятие информации.

Что такое диаграмма по математике

Диаграмма по математике может использоваться для решения различных задач. Например, с помощью круговой диаграммы можно представить процентное соотношение разных категорий или групп. Столбчатая диаграмма позволяет сравнить значения разных показателей или наблюдений. Линейная диаграмма помогает отследить изменение значения величины во времени.

Для создания диаграммы по математике необходимо собрать данные, организовать их и выбрать подходящий тип диаграммы. Затем следует построить оси и отметить значения на них. После этого можно нарисовать соответствующие элементы диаграммы и подписать их.

Диаграмма по математике помогает визуализировать информацию и делает ее более понятной и доступной для анализа. Она может быть полезна не только в математике, но и в других областях, таких как экономика, статистика, бизнес и многих других.

Основные понятия

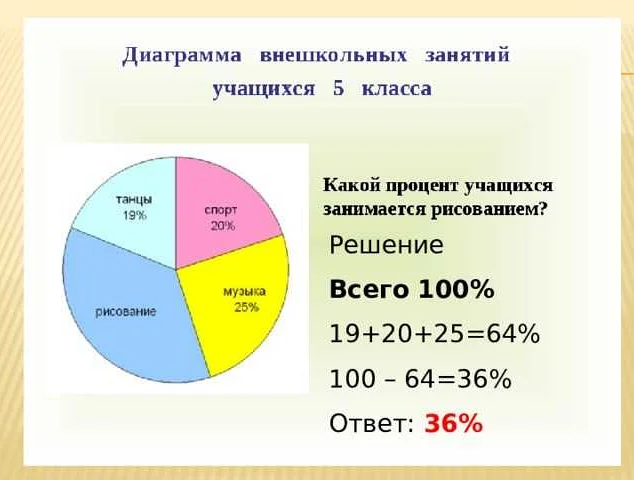
Круговая диаграмма – это диаграмма, представленная в виде круга, разделенного на секторы. Каждый сектор представляет определенную часть или долю от всего.

Ключ – это обозначение или пояснение, которое помогает понять значения символов, цветов или других элементов на диаграмме.

Легенда – это часть диаграммы, содержащая ключ и пояснения к различным элементам.

Данные – числовые значения или факты, которые отображаются на диаграмме.

Оси – это линии на диаграмме, которые помогают ориентироваться и измерять значения данных.

Шкала – это деления на осях, которые позволяют определить значения данных на диаграмме.

Процент – это доля или часть от целого, выраженная в процентах. На круговых диаграммах проценты используются для отображения доли каждого сектора от общего значения.

Диаграмма сравнения – это диаграмма, которая позволяет сравнить размеры или значения различных объектов или явлений.

Диаграмма сетки – это диаграмма, состоящая из сетки, где каждая ячейка представляет определенное значение.

Диаграмма временной шкалы – это диаграмма, отображающая изменение значений во времени.

Диаграмма роста – это диаграмма, показывающая изменение значения величины с течением времени.

Диаграмма спуска и подъема – это диаграмма, показывающая колебания величины в течение определенного периода времени.

Круговая диаграмма

Круговая диаграмма часто используется для наглядного отображения относительных величин различных категорий или составляющих целого. Она позволяет сравнить вклад каждой категории в общую сумму или процентное соотношение различных составляющих.

В круговой диаграмме данные представлены в виде угловых секторов, пропорциональных их значениям. Каждый сектор имеет свой цвет или шаблон, чтобы обозначить соответствующую категорию или составляющую.

Примеры использования круговых диаграмм:

• Представление распределения бюджета на различные категории расходов.
• Отображение соотношения продаж различных товаров или услуг.
• Иллюстрация процентного соотношения населения по возрастным группам.

Круговая диаграмма помогает визуализировать данные и делает их более понятными и запоминающимися. Она может быть полезным инструментом в анализе и презентации информации.

Столбиковая диаграмма

Столбиковая диаграмма состоит из следующих элементов:

1. Ось Y – вертикальная ось, на которой откладываются значения. Она показывает величину или количество.
2. Ось X – горизонтальная ось, на которой отмечаются категории или периоды времени. Она служит для сравнения данных между разными категориями.
3. Столбцы – вертикальные прямоугольники, высота которых соответствует значению. Они располагаются на оси X и показывают величину каждой категории.
4. Заголовок – краткое название диаграммы, которое описывает представленные данные.

Столбиковые диаграммы часто используются для сравнения данных, представления процентных соотношений, анализа трендов и показа распределения по категориям.

Примеры использования столбиковой диаграммы:

• Сравнение продаж разных товаров за определенный период времени.
• Представление результатов голосования по разным кандидатам.
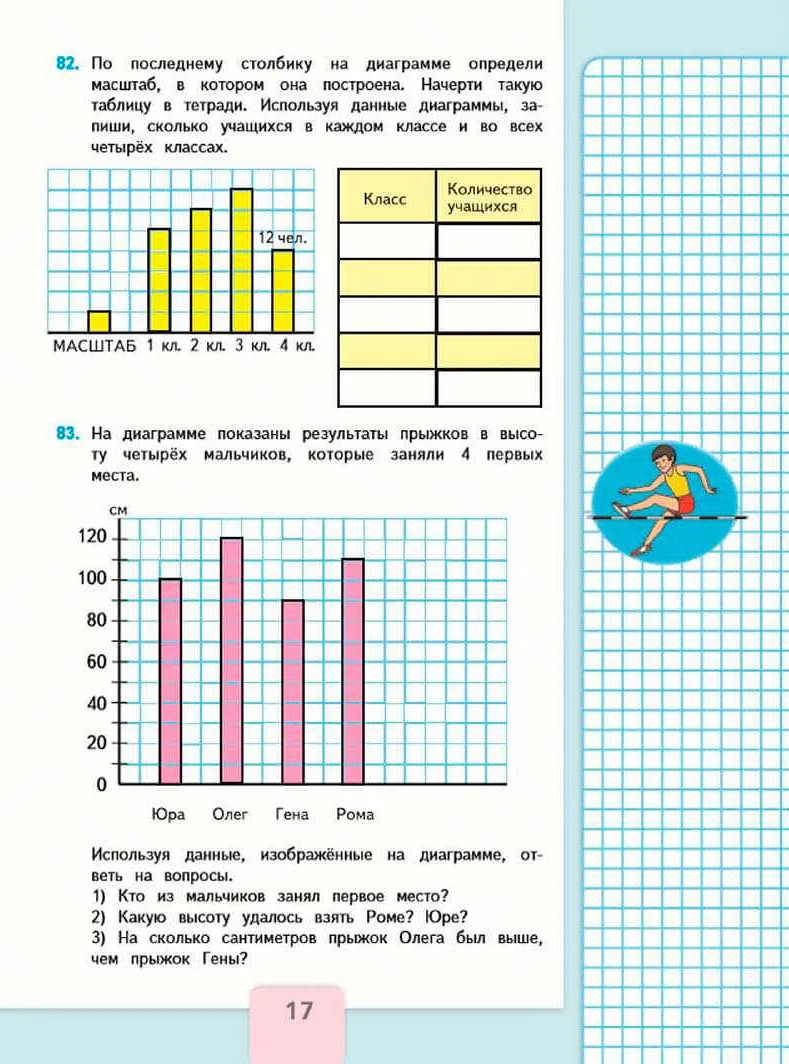
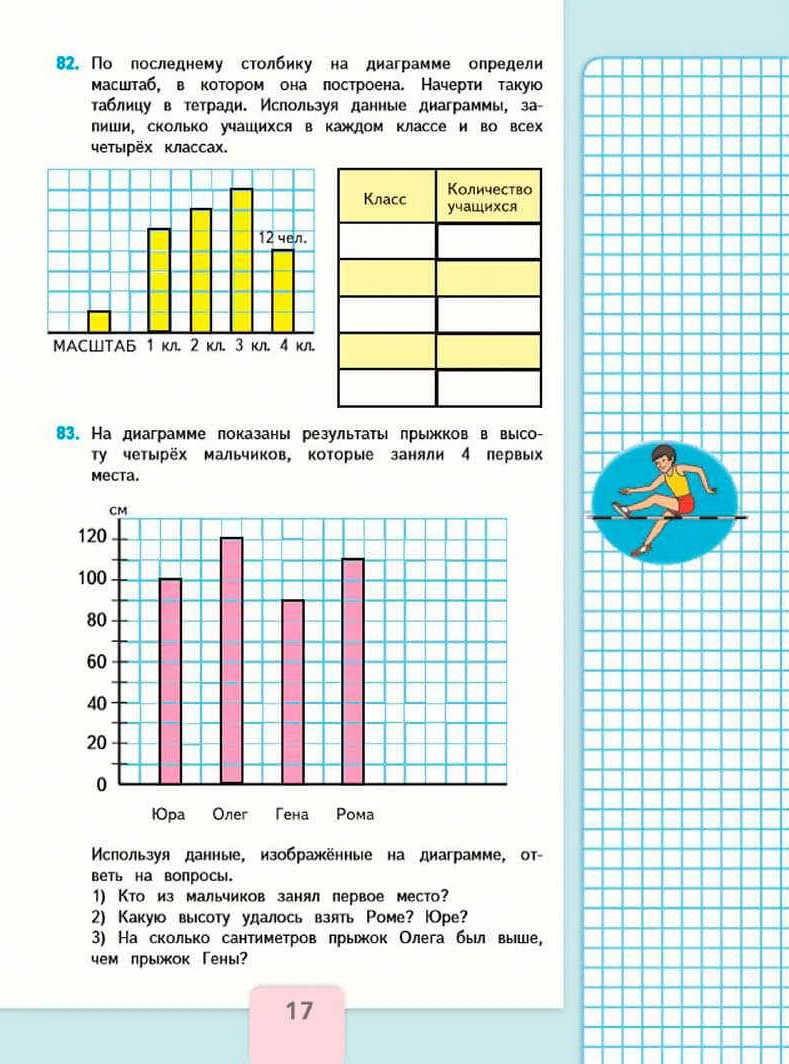
• Отображение количества студентов в каждом классе школы.

Столбиковая диаграмма является важным инструментом визуализации данных и помогает легче понять и анализировать информацию.

Гистограмма

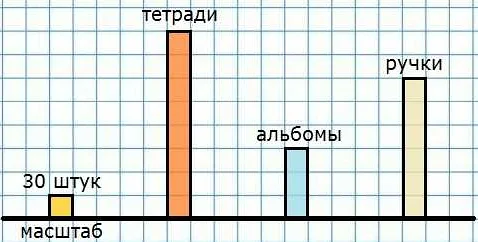
Для построения гистограммы необходимо выполнить следующие шаги:

1. Выбрать интервалы или диапазоны значений, на которые будет разделена шкала гистограммы.
2. Подсчитать количество значений, попадающих в каждый из интервалов.
3. Построить столбцы, где высота каждого столбца будет соответствовать количеству значений в соответствующем интервале.
4. Подписать оси гистограммы и добавить необходимые пояснения.

Гистограммы используются для визуализации статистических данных, а также для сравнения и анализа различных наборов данных. Они позволяют увидеть распределение значений и выявить основные характеристики набора данных, такие как мода, медиана, среднее значение и дисперсия.

Пример использования гистограммы:

1. Представим, что у нас есть данные о росте учеников в классе.
2. Мы решаем построить гистограмму, чтобы узнать, какое количество учеников находится в различных диапазонах роста.
3. Мы выбираем интервалы роста (например, 130-140 см, 140-150 см, и т.д.) и подсчитываем количество учеников, попадающих в каждый из этих интервалов.
4. Затем мы строим столбцы, где высота каждого столбца соответствует количеству учеников в соответствующем интервале.
5. Мы подписываем оси гистограммы (ось X — интервалы роста, ось Y — количество учеников) и добавляем необходимые пояснения.

Таким образом, гистограмма позволяет наглядно представить данные и сделать выводы о распределении значений.

Примеры использования

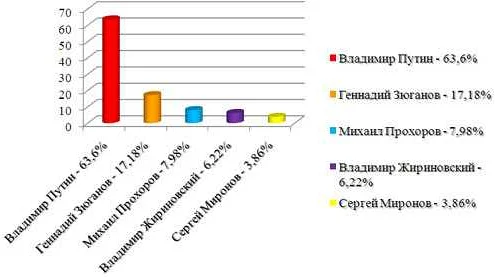
Диаграмма может быть использована для визуализации данных и сравнения их величин. Например:

Список предметовКоличество учеников

Математика	15
Русский язык	10
История	8

На приведенной выше диаграмме показано количество учеников, изучающих разные предметы. Можно наглядно увидеть, что наибольшее количество учеников изучает математику, затем идет русский язык, а самое маленькое количество учеников изучает историю.

Также диаграмма может использоваться для отображения процентного соотношения разных категорий. Например:

КатегорияПроцент

Фрукты	40%
Овощи	30%
Мясо	20%
Молочные продукты	10%

В данном случае диаграмма показывает процентное соотношение разных категорий продуктов. Например, фрукты составляют 40%, овощи — 30%, мясо — 20%, а молочные продукты — 10%.

Диаграмма количества фруктов

Диаграмма количества фруктов может быть представлена в виде круговой диаграммы или столбчатой диаграммы.

Круговая диаграмма показывает долю каждого вида фруктов в общем количестве. Каждый сектор круга соответствует определенному виду фруктов, а его размер пропорционален количеству этого вида фруктов.

Столбчатая диаграмма показывает количество каждого вида фруктов на оси Y, а на оси X отмечены названия видов фруктов. Каждый столбец соответствует определенному виду фруктов, а его высота пропорциональна количеству этого вида фруктов.

Например, если мы хотим представить данные о количестве яблок, груш и апельсинов, то на круговой диаграмме каждый сектор будет соответствовать одному виду фруктов (яблоки, груши, апельсины), а его размер будет отражать их долю в общем количестве. На столбчатой диаграмме каждый столбец будет соответствовать одному виду фруктов, а его высота будет показывать количество фруктов этого вида.

Диаграмма количества фруктов может быть полезной при анализе данных о фруктах, сравнении их количества и визуализации результатов. Она помогает легче увидеть различия между разными видами фруктов и сделать выводы о их распределении.

Диаграмма успеваемости учеников

Для построения диаграммы успеваемости учеников используется таблица с указанием оценок каждого ученика по разным заданиям или темам. Каждая оценка обозначается определенным цветом или символом, что помогает легко визуализировать различные уровни успеваемости.

Примеры оценок, которые могут быть использованы для построения диаграммы успеваемости учеников:

ОценкаЦветОбозначение

5		Отлично
4		Хорошо
3		Удовлетворительно
2		Неудовлетворительно

Используя диаграмму успеваемости учеников, можно сравнить результаты каждого ученика и общую успеваемость класса. Это помогает учителю более точно оценить уровень знаний учеников и принимать меры для дальнейшего обучения.

Построение диаграммы успеваемости учеников – это важный инструмент для анализа и контроля учебного процесса. Она помогает выявлять проблемы и успехи в обучении каждого ученика, а также определять необходимые корректировки в методиках и подходах преподавания.

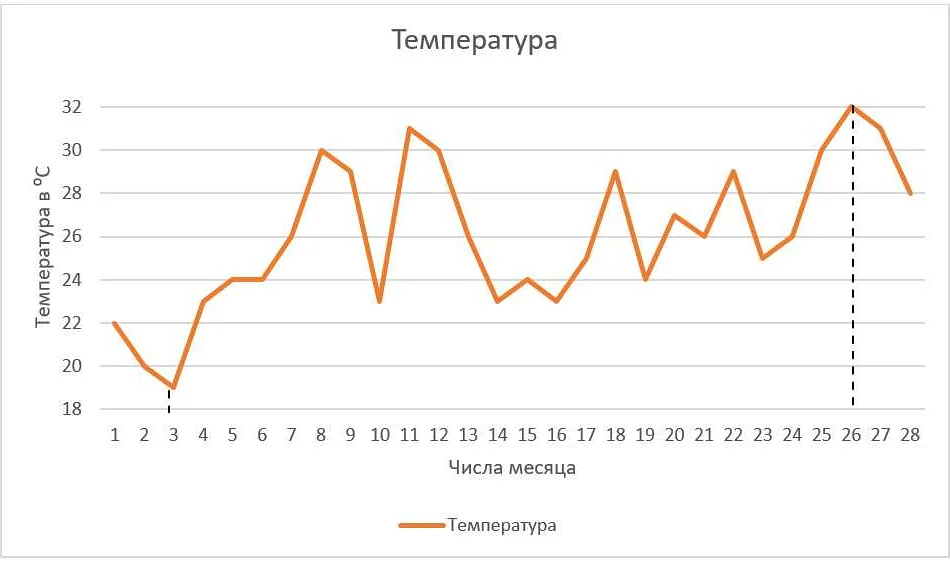
Диаграмма погодных условий

В диаграмме погодных условий используются различные символы и цвета для обозначения разных погодных явлений. Например, солнце может быть изображено желтым кругом, а дождь – синими вертикальными линиями.

Диаграмма погодных условий может быть полезна для прогнозирования погоды, планирования активностей на открытом воздухе и анализа климатических условий разных регионов. Она позволяет быстро и наглядно оценить, какие погодные условия ожидаются в определенный день или период времени.

Примеры диаграмм погодных условий могут включать информацию о температуре воздуха, осадках (дожде, снеге, граде), облачности, ветре, влажности и давлении. Каждый показатель может быть представлен отдельным символом или цветом.

Например, на диаграмме погодных условий в солнечный день будет изображено солнце, температура будет отображаться числом, а ветер – стрелкой, указывающей направление и силу ветра.

Диаграмма погодных условий – это важный инструмент, который помогает людям получать информацию о погоде в удобном и понятном формате. Она позволяет быстро и эффективно оценить текущие и будущие погодные условия, что помогает принимать соответствующие решения и планировать свои действия.

Диаграмма продаж товаров

Для создания диаграммы продаж товаров необходимо:

1. Выбрать период времени, за который будут анализироваться продажи.
2. Составить список товаров, продажи которых будут отображены на диаграмме.
3. Записать данные о количестве проданных единиц каждого товара за выбранный период времени.
4. Посчитать долю каждого товара в общем объеме продаж.
5. Последовательно отображать на диаграмме доли продаж каждого товара в виде секторов круга или столбцов.

Пример использования диаграммы продаж товаров:

• Предположим, что у нас есть магазин, который торгует различными видами фруктов: яблоками, грушами, апельсинами и бананами.
• За последний месяц было продано следующее количество единиц каждого товара: яблок — 50, груш — 30, апельсинов — 40, бананов — 20.
• Для создания диаграммы продаж товаров мы рассчитываем долю каждого фрукта в общем объеме продаж: яблок — 35%, груш — 21%, апельсинов — 28%, бананов — 14%.
• На диаграмме будут отображены секторы круга, соответствующие долям продаж каждого фрукта.

Диаграмма продаж товаров позволяет с легкостью сравнивать объемы продаж различных товаров и выявлять наиболее популярные или непопулярные товары. Она помогает в принятии решений по улучшению товарного ассортимента и разработке маркетинговых стратегий.

Вопрос-ответ:

Какая цель использования диаграммы в математике?

Основная цель использования диаграммы в математике — визуализация информации, представление данных в удобной форме. Диаграммы помогают увидеть связи между различными элементами и понять основные понятия математики.

Какие типы диаграмм используются в математике?

В математике используются различные типы диаграмм, включая столбчатые диаграммы, круговые диаграммы, линейные диаграммы и графики. Каждый тип диаграммы используется для визуализации определенного вида данных.

Как построить столбчатую диаграмму?

Для построения столбчатой диаграммы необходимо выбрать ось X и ось Y, где ось X представляет собой категории, а ось Y — значения. Затем на оси X отмечаются категории, а на оси Y — значения. После этого строятся прямоугольники, высота которых соответствует значениям, их представляющим. Наконец, прямоугольники раскрашиваются и подписываются.

Как использовать диаграмму для сравнения данных?

Для сравнения данных с помощью диаграммы необходимо визуализировать данные на диаграмме и сравнить их. Можно сравнить высоту столбцов в столбчатой диаграмме, длину линий в линейной диаграмме или площади секторов в круговой диаграмме. Сравнивая значения, можно получить представление о различиях и сходствах между данными.

Видео по теме: